引言
前面三篇文章介绍了变分推断(variational inference),这篇文章将要介绍变分自编码器,但是在介绍变分自编码器前,我们先来了解一下传统的自编码器。
自编码器
自编码器(autoencoder)属于无监督学习模型(unsupervised learning),更严格地说属于自监督学习(self-supervised learning)。在自监督学习中,预测的目标来自输入数据本身,不需要人工标定——有监督学习(supervised learning),例如图像分类任务,需要人工标注图像中的物体是猫还是狗或者是其他东西。自编码器简单地说,就是实现将$x$转换为$y$,再将$y$转换回$x$的模型,如$(图1)$所示。
自编码器主要由编码器(encoder)和解码器(decoder)两个模块组成。编码器的任务是将输入数据编码成某种表征,而解码器的任务是将编码器的输出作为输入,将其解码成目标数据。不过Encoder-decoder的结构不仅用于自编码器,在普通的分类和回归任务上都有运用。例如,机器翻译中,编码器将原语言编码成隐表征,然后解码器再将隐表征翻译到目标语言,也就是一个由$x$到$y$再到$z$的过程。
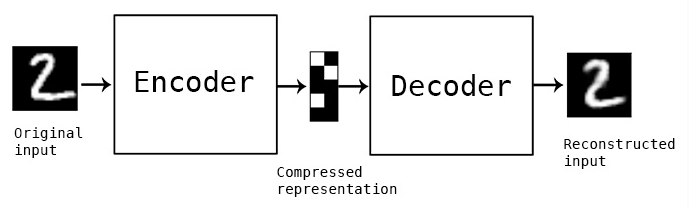
(图1,来自https://blog.keras.io/building-autoencoders-in-keras.html)
自编码器的预测目标是输入本身,模型训练的目标是减小输出与输入的差异,可以表示为:
\begin{equation} \argmin_{E,D} E[L(x, D(E(x)))] \nonumber \end{equation}
其中$ \argmin_{E,D}$表示取编码器$E$和解码器$D$,使重构的$x$与原$x$差异尽可能小,也就是最小化重构误差$L$。这样的模型并不能直接用于我们常见的分类或回归这样的任务,因为这些任务的输出与输入是不同的。自编码器更多的是用来对数据进行降噪(denoising)——如$(图2)$所示,或者实现数据降维(dimension reduction)、数据压缩(compression)——例如将10维的向量转换为2维的向量——或者是作为其他模型的一个模块,例如通过对输入进行特定处理,从而让模型学习某些特定的数据表征(latent representation)。
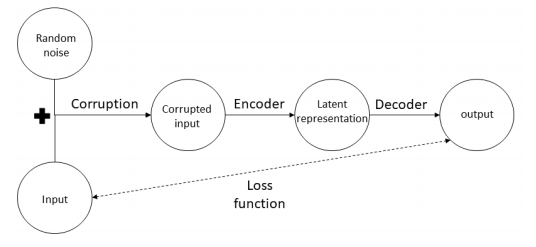
(图2,来自论文《autoencoders》)
自编码器的实现
实现自编码器的方法有几种,大体上可以分为欠完备自编码器(undercomplete autoencoder)和正则化自编码器(regularited autoencoder)。
欠完备自编码器
欠完备自编码器,是通过在输入层和输出层之间插入一个维度较低的瓶颈层(bottleneck)——例如输入层和输出层的维度都是700,而瓶颈层的维度是30——或者采用维度逐层递减的编码器,和维度逐层递增的解码器组成的模型。插入瓶颈层的自编码器又称为香草自编码器(vanilla autoencoder)——香草通常表示最简单的方法。
原始的自编码器是多层感知机(MLP),内部采用的是全连接层,在处理图像数据的时候,将全连接层替换为卷积层通常能得到更好的结果,而在处理序列型数据的时候,我们则可以采用RNN等序列模型。另外,当编码器和解码器都是线性模型,例如我们把神经网络中的非线性的激活函数去掉,此时自编码器就是线性自编码器。如果在训练线性自编码器时采用平方误差损失函数(squared error cost function),那么编码器输出的隐表征与主成分分析(Principal Component Analysis,PCA)相似(赶时间,暂时不推导了,请参考论文$[1]$)。
正则化自编码器
正则化的方法有很多,例如可以使用L1正则化对神经网络的激活函数的输出进行处理。假设多多层感知机有三层,我们只对之间那层进行约束,那么自编码器的目标函数为:
\begin{align} &\argmin_{E,D} E[L(x, D(E(x)))] + \lambda \sum_i {|\bar{a}_i|} \nonumber \\ & \bar{a}_i = \frac{1}{n} \sum_j^n {a_i(x_j)} \end{align}
其中$\lambda$是超参数,由人设定,$a_i$是中间层第$i$个激活函数的输出,它是对$n$个数据计算后求平均的结果,$|·|$是L1正则化。
L1正则化方法需要设置超参数$\lambda$,如果采用KL散度来对激活函数进行约束,则可以避免设置超参数——要设其实也可以。在这种方法中,我们将激活函数的输出看成伯努利分布(Bernoulli distribution)——样本为1或0,为1的概率为$p$,$0<p<1$,这和sigmoid函数的取值范围一致。这样,自编码器的目标函数就变为:
\begin{align} &\argmin_{E,D} E[L(x, D(E(x)))] + \sum_i {KL(p \parallel \hat{p}_i)} \label{1} \\ & \hat{p}_i = \frac{1}{n} \sum_j^n{a_i(x_j)} \nonumber \end{align}
其中$\hat{p}_i$对应第$i$个激活函数对$n$个数据的平均值,$p$为是一个较小的值(例如0.05),这样就可以使神经元变得稀疏(值趋近于0),所以这种方法与L1正则化是相似的。
另一种正则化的模型是CAE(Contractive AutoEncoder)。这是由Bengio等人提出来的,它的目标是降低模型对数据波动的敏感度。在GAN专题的介绍WGAN的篇章,有一个概念叫Lipschitz约束:
\begin{equation} \frac{\parallel f(x_1) - f(x_2) \parallel}{\parallel x_1 - x_2 \parallel} \leq k \nonumber \end{equation}
其中$k$是某个值,等号左边要小于等于它。使模型满足这种约束的一种方法是梯度惩罚(gradient penalty),因为上面的式子可以认为是在计算梯度的绝对值。梯度,也就是一阶导,从向量和矩阵的角度讲,就是雅可比矩阵(Jacobian matrix)。CAE模型也是要对Jacobian矩阵进行约束,从而使模型更加鲁棒(robust),不会对数据太敏感。CAE的目标函数如下:
\begin{equation} \argmin_{E,D} E[L(x, D(E(x)))] + \lambda \parallel J_E(x) \parallel_2^2 \nonumber \end{equation}
其中$\parallel J_E(x) \parallel_2^2$是计算雅可比矩阵的Frobenius范数,$J_E(x)$是Jacobian矩阵,它的基本形式如下:
\begin{bmatrix} \frac{\partial h_1}{\partial x_1} & \frac{\partial h_1}{\partial x_2} & \dotsb & \frac{\partial h_1}{\partial x_n} \\ \frac{\partial h_2}{\partial x_1} & \frac{\partial h_2}{\partial x_2} & dotsb & \frac{\partial h_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial h_n}{\partial x_1} & \frac{\partial h_n}{\partial x_2} & dotsb & \frac{\partial h_n}{\partial x_n} \end{bmatrix}
而Frobenius范数是矩阵所有元素$J_{i,j}=\triangledown_{x_i} h_j(x_i)$的平方和再取平方根$\sqrt{\sum_{i,j}{J_{i,j}^2}}$,$h_j$是第$j$个神经元$h = a(Wx + b)$。
变分自编码器
式$(\ref{1})$向我们展示了自编码器目标函数的一种构造方法,其中KL散度作为正则项(regularizer)去控制模型内部的神经元。我们可以将$(\ref{1})$中的KL散度用另一个KL散度替换:
\begin{equation} \argmin_{E,D} E[L(x, D(E(x)))] - \sum_i {KL(q(z|x) \parallel p(z|x))} \label{2} \end{equation}
其中$q(z|x)$是变分分布,$p(z|x)$是真实的后验分布,$z$是隐变量。就像前面文章说的,我们可以把分类任务中的标签看作隐变量,所以$p(z|x)$是通过$x$推断标签$z$。另外,式中的变分分布$q(z|x)$也可以是$q(z)$的形式,也就是不以$x$作为条件,但我们这里以$q(z|x)$作为编码器。

(图3,来自https://towardsdatascience.com/intuitively-understanding-variational-autoencoders-1bfe67eb5daf)
式$(\ref{2})$并不是变分自编码器的目标函数,因为就像前面的文章中提到的,后验$p(z|x)$是难以计算的,要得到变分自编码器的目标函数,我们要用$ELBO$替换了这里的KL散度。$ELBO$的数学表示如下:
\begin{align} ELBO(q) &= E_q [\log{p(x|z)} ] - KL(q(z|x) \parallel p(z)) \label{3} \\ &= E_q [\log{p(z,x)} ]- E_q [\log{q(z)} ] \label{4} \end{align}
其中$p(x|z)$是似然,可以看作是解码器,$p(z)$是隐变量$z$的先验(prior)。优化式$(\ref{3})$,可以看作是求最大似然(maximum likelihood),同时最小化KL散度。(提一点,仅仅从理论上看,因为似然可以看作的解码器,变分自编码器并不需要一个真正的解码器模块存在,也就是说式$(\ref{2})$前面的重构误差可以不要,所以一些文章认为变分自编码器不是真正意义上的自编码器。)
为了求解$ELBO$,我们需要对$z$进行采样。假设$z \sim q(z|x)=N(\mu,\sigma^2)$服从某个高斯分布,也就是说我们把高斯分布作为$q(z|x)$的族,优化$ELBO$就是求高斯分布的参数$\mu$和$\sigma^2$,使$ELBO$最大。得到参数$\mu$和$\sigma^2$后,我们就可以从高斯分布中采样$z$。具体方法是通过$z=g(\epsilon, x)=\mu + \sigma \epsilon$。这里$\epsilon$是一个随机噪音,服从高斯分布$N(0,I)$,也就是说向量$\epsilon$中的元素的值在[0,1]区间。这样设置$\epsilon$,采样得到的$z$能够服从$N(\mu,\sigma^2)$分布。这个采样过程如$(图3)$所示。我们用某个函数$g(\epsilon,x)$代替$q(z|x)$,用$\mu$和$\sigma$代替$z$。这是一种重参数化(reparameterization)的方法——重参数化在GAN专题中介绍参数归一化(weight normalization)时也有提到。
经过重参数化,并且采用stochastic的策略,我们就将$ELBO$变为:
\begin{align} &ELBO= \frac{1}{M} \sum_{m=1}^M {\log{p(x_i, z_{i,m})}} - \log{q(z_{i,m},x_i)} \nonumber \\ &z_{i,m} = g(\epsilon_{i,m}, x_i) \nonumber \end{align}
因为式$(\ref{3})$中的KL散度是可以求解析解的,所以也可以采用下面的式子:
\begin{align} &ELBO = \frac{1}{M} \sum_{m=1}^M {\log{p(x_i| z_{i,m})}} -KL(q(z|x) \parallel p(z)) \nonumber \\ &z_{i,m} = g(\epsilon_{i,m}, x_i) \nonumber \end{align}
其中$M$是批数据的数据量,它可以是较小的值,甚至是1。
进阶实例
为了能够更深入地理解自编码器,这里我们对一篇论文中的模型进行介绍。这篇论文是$[2]$。在这篇论文中,作者介绍了自编码器的一种特殊形式,ALAE,它结合了自编码器和GAN两种模型,(如图4所示)。
相比于传统的自编码器,编码器与解码器的目标是将输入的$x$转换成隐藏层$h$(论文中的$w$),然后再将$h$转化为$x$,这里的自编码器则是实现数据从$h$的隐分布(latent distribution)到$x$对应的真实数据分布,最后再输出服从$h$的分布的数据的过程。
但是在$h \to x \to h$这样的编码解码模式下,服从隐分布的数据$h$来自哪呢?作者团队采用了GAN的生成器的方法,预先设定一个分布,然后通过生成器$F$将此分布的数据$z$映射到$h$的隐分布,这样就得到了$h$,剩下的就是将$h$转换为$x$再转化为$h$。
有了$h$,现在的问题是,如何保证模型生成的$x$服从真实的$x$的分布呢?为了解决这个问题,作者采用了GAN中的对抗机制(adversary)。来自真实数据的$x$和生成的$x$一样,都会经过解码器$E$转换成$h$,生成的$h$会作为判别器$D$的输入。判别器$D$的作用是尽可能的分辨$h$是来自真实的$x$还是生成的$x$,而判别器$D$之前的模型相对于GAN的生成器,目标是使两种$h$的分布尽可能一致,使判别器$D$难以分辨。通过这样的对抗机制,模型就能保证生成的$x$的分布接近真实的分布。
为了保证经过编码转换为$x$后,再经过解码能返回原先的$h$,模型在优化的时候,需要减小输入的$h$与解码得到的$h$的差异。另外,为了让模型更具有普遍性,编码器$G$的输入除了$h$,还有噪音 。
在应用预测的时候,模型的模块会重新组织,与传统的自编码器一致(如图4中的Inference)。真实数据,例如图像,会经过上面的解码器$E$(在这里作为编码器),生成隐藏层$h$,然后$h$再经过上面的编码器$G$(这里作为解码器)输出最终的结果,也就是图像或其他真实数据。
对于论文中,模型在训练和在预测的时候采用不同的组织方式,原因是这样能够更有效地运用正则化处理。以传统的自编码器的训练方式,进行正则化处理,数据经过编码器和解码器输出的结果质量会变差。例如在图像处理中,输出的图像会变得模糊。但如果是对隐藏分布进行正则化处理,就不会有这样的限制。选择任何方式,只会对隐藏分布产生影响,都不会对真实数据的分布产生太大的影响。
除了基础的ALAE模型,作者还借鉴了StyleGAN——在GAN专题的最后一篇中有介绍——设计了StyleALAE。在StyleALAE中,作者将$H$作为中间隐藏空间(intermediate latent space)。数据$z$在$F$中的各层通过实例标准化层(IN,Instance Normalization layer)转化为对应的实例均值和标准差,作为这一层的风格(style)。这些风格信息在经过AdaIN(Adaptive Instance Normalization layer)生成$h$,然后与噪音一起,经过卷积层转化为$x$。
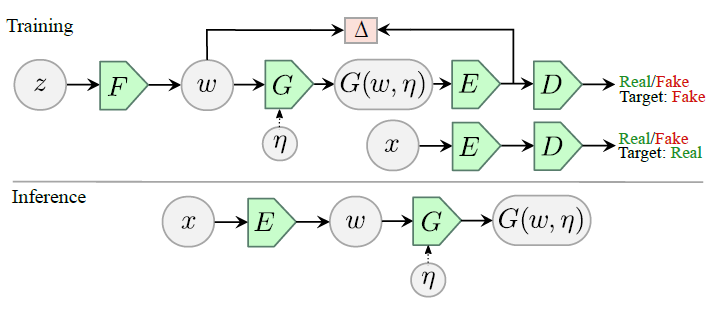
(图4,来自论文《adversarial latent autoencoders》)
[1] Plaut, E. (2018). "from_principal_subspaces_to_principal_components_with_linear_autoencoders".
[2] Pidhorskyi, S., Adjeroh, D., A., Doretto, G. (2020). "Adversarial Latent Autoencoder".


 浙公网安备 33010602011771号
浙公网安备 33010602011771号