SVI
变分推断的前两篇介绍了变分推断的构造方法、目标函数以及优化算法CAVI,同时上一篇末尾提到,CAVI并不适用于大规模的数据的情况,而这一篇将要介绍一种随机优化(stochastic optimization)的方法。这种优化方法与随机梯度下降(Stochastic Gradient Descent,SGD)方法有相近,它能够处理大规模数据。通过这种方法进行优化的变分推断,我们称为随机变分推断(Stochastic Variational Inference,SVI)。(需要注意的是,这里介绍的是一种通用优化算法,并不局限于优化变分推断)
随机梯度下降
梯度下降是广泛用于机器学习,尤其是深度学习模型训练的优化算法之一——关于优化算法,以后会开一个专题来介绍。在处理大规模数据时,我们可以采用随机梯度下降法,分批次地处理小规模数据。梯度下降法采用下面的方式优化模型的参数:
\begin{align} &\theta^{t+1} = \theta^t - \eta \frac{\partial f}{\partial \theta} \label{1.13} \\ &\frac{\partial f}{\partial \theta} = \begin{bmatrix} \frac{\partial f}{\partial \theta_1} & \frac{\partial f}{\partial \theta_2} & ⋯ & \frac{\partial f}{\partial \theta_k} \end{bmatrix}^T \nonumber \\ & \theta^t = \begin{bmatrix} \theta_1^t & \theta_2^t & ⋯ & \theta_k^t \end{bmatrix}^T \nonumber \end{align}
其中$\theta^t$是当前参数的值(一系列参数$\theta_1^t,\theta_2^t,⋯,\theta_k^t$组成的向量),$\theta^{t+1}$是第$t+1$次优化后的参数的值,$\eta$是超参数(hyper parameter)学习率(learning rate),由人设定,而$\frac{\partial f}{\partial \theta}$是函数$f$对参数$\theta$的梯度(或者说一阶导数)。当移动$\Delta \theta$能够使函数的值变小,也就是梯度为负值,那么参数$ \theta^t$就会向$\Delta \theta$方向移动,值变为$\theta^{t+1}$,这样函数的值就会越来越小,最终得到局部最小值(如果函数是非凸函数,有多个极值,否则得到全局极值),如$(图4、5)$所示。
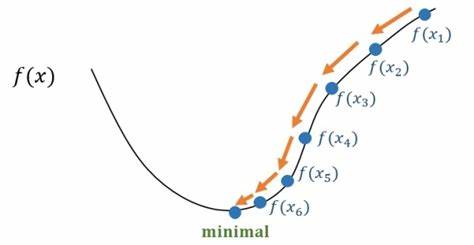
(图4,来自zhuanlan.zhihu.com/p/36564434)
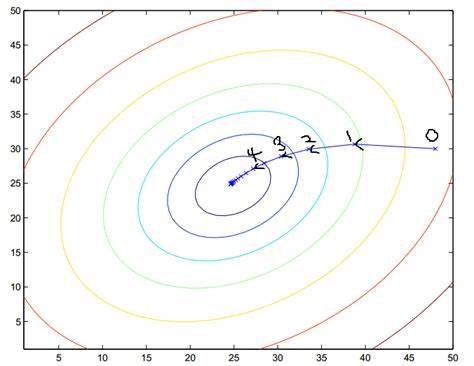
(图5,来自https://blog.csdn.net/zhulf0804/article/details/52250220)
黎曼测度
上面的方法是标准的梯度下降法,可以看到梯度的计算采用的是欧式距离(Euclidean distance,欧几里得距离)。当参数$\theta_1^t$移动$\Delta \theta_1$,参数$\theta_2^t$移动$\Delta \theta_2$,其他参数以相同方式移动,那么函数$f$移动的欧式距离是:
\begin{align} d(\theta,\theta+\Delta \theta) = \sqrt{\sum{\Delta \theta_i}} = \sqrt{\Delta \theta^T \Delta \thetaθ} = \parallel \Delta \theta \parallel_2 \label{1.14} \end{align}
$(\ref{1.14})$式中$\Delta \theta^T \Delta \theta$表示向量点积(inner product),$\parallel \Delta \theta \parallel_2$是欧式范数(Euclidean norm),又称L2范数。如$(图5)$所示,从0点移动到1点,在x轴和y轴分别移动$\theta_1$和$\theta_2$。
但是,欧式距离并不适用于所有情况,因为参数可能并不在欧式空间(Euclidean space)中。例如,从$\theta_1^t$移动$\Delta \theta_1$到$\theta_1^{t+1}$,和从$\theta_1^{t+1}$移动$\Delta \theta_1$到$\theta_1^{t+2}$,从欧式距离来看都是移动了$\Delta \theta_1$,但在非欧空间中,两个$\Delta \theta_1$可能是不同的。看$(图6)$的例子,上下两个图都是从红色分布移动到绿色分布,从均值(mean)来看,都是从-1变为1,移动了2,但是$(图6)$的上面的图中,在某种意义上,分布发生的变化要比下图中的变化大。对这样的情况,我们引入黎曼几何(Riemannian geometry)。
在黎曼几何中,两点的距离不是通过欧式范数$(\ref{1.14})$来计算的,而是通过:
\begin{align} d(\theta, \theta+\Delta \theta) &= \sqrt{\sum_i{\sum_j{\Delta \theta_i \Delta \theta_j g_{i,j} (w)}}} \nonumber \\ &= \sqrt{\Delta \theta^T G(\theta) \Delta \theta} \label{1.15} \end{align}
其中$G(\theta)$是黎曼测度张量(Riemannian metric tensor),它由$\theta$决定——这里不做详细的推导了,可以参考论文$[3]$的section 3的Example,论文中的式(15)。另外,当$G(\theta)$为单位矩阵时——从左上角到右下角的对角线上的值都为1,其他位置的值都为0的矩阵——$(\ref{1.15})$等于$(\ref{1.14})$,此时计算的是欧式距离。
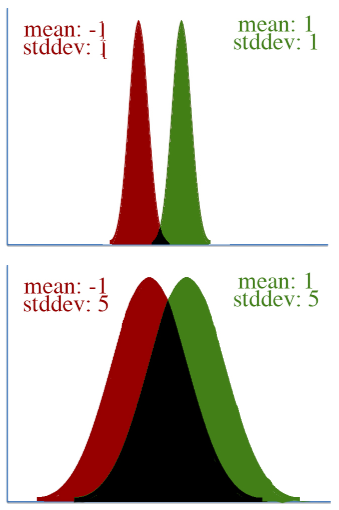
(图6,来自http://kvfrans.com/what-is-the-natural-gradient-and-where-does-it-appear-in-trust-region-policy-optimization/)
直觉上,$G(\theta)$描述了几何空间对两点间的路径的影响。例如,在黎曼几何的一个经典应用案例,广义相对论中,光线在引力场中发生了弯曲,而不是直线行走。
Fisher信息矩阵
从$(图6)$的例子可以看到,采用欧式距离来衡量概率分布的变化量不是一个好主意。分布的差异我们更多的是通过KL散度等指标来衡量。当$\theta$是分布的参数,而且我们用KL散度来衡量两个分布的差异时,上面介绍的黎曼测度张量$G(\theta)$就是Fisher信息矩阵(Fisher Information Matrix,FIM):
\begin{equation} F=E_{p(\theta)} [\triangledown \log{p(\theta)} \triangledown \log{p(\theta)}^T ] \label{1.16} \end{equation}
其中$\triangledown$表示一阶导。
为了证明在KL散度作为距离指标时,Fisher信息矩阵是黎曼测度张量$G(\theta)$,我们先来看一下KL散度的泰勒展式。泰勒展式的通用形式如下:
\begin{equation} f(x_0+ \Delta x)=f(x_0 )+ \Delta x f' (x_0 )+ \Delta x^2 f'' (x_0 )+⋯ \nonumber \end{equation}
其中$f'$为函数$f$的一阶导,$f''$为函数的二阶导,$\Delta x^2$为移动距离$\Delta x$的平方。等号右边如果去掉省略号部分,则表示是二阶泰勒展式,如果只保留前两项,则是一阶泰勒展式。KL的泰勒展式为:
\begin{align} KL(q(\theta+ \Delta \theta) \parallel p(\bar{\theta})) &=KL(q(\theta) \parallel p(\bar{\theta})) \nonumber \\ &+ (\triangledown_{\theta} KL(q(\theta) \parallel p(\bar{\theta})))^T \Delta \theta \nonumber \\ &+ \frac{1}{2} \Delta \theta^T \triangledown_{theta}^2 KL(q(\theta) \parallel q(\bar{\theta}))\Delta \theta + \dotsb \label{1.17} \end{align}
其中$\bar{\theta}$是固定的值,$\theta$才是自变量,$\triangledown_{\theta}$表示一阶导,$\triangledown_{\theta}^2$表示二阶导。简化$(\ref{1.17})$,得到:
\begin{align} KL(q(\theta+\Delta \theta) \parallel q(\bar{\theta})) &\approx KL(q(\theta) \parallel p(\bar{\theta})) \nonumber \\ &+ \triangledown_{\theta} E_{q(\theta)} [\log{q(\theta)} ]^T \Delta \theta \nonumber \\ &- \frac{1}{2} \Delta \theta^T F \Delta \theta \label{1.18} \end{align}
其中$(\ref{1.17})$等号右边第二项到$(\ref{1.18})$等号右边第二项的推导如下:
\begin{align} \triangledown_{\theta} KL(q(\theta) \parallel q(\bar{\theta})) &= \triangledown_{\theta} E_{q(\theta)} [\log{q(\theta)}] - \triangledown_{\theta} E_{q(\theta)} [\log{p(\bar{\theta})} ] \nonumber \\ &= \triangledown_{\theta} E_{q(\theta)} [\log{q(\theta)}] = 0 \label{1.19} \end{align}
因为第一行等号右边第二项中的$\log{q(\bar{\theta})}$对$\theta$是常数,求导结果为0。最终$(\ref{1.19})$为0,因为:
\begin{align} \triangledown_{\theta} E_{q(θ)} [\log{q(\theta)} ] &= E_{q(θ)} [∇_θ logq(θ) ] \nonumber \\ &= \int{q(\theta) \triangledown_{\theta} \log{q(\theta)}} d\theta \nonumber \\ &=\int{q(\theta) \frac{\triangledown_{\theta} q(\theta)}{q(\theta)} } d\theta \nonumber \\ &= \int{\triangledown_{\theta} q(\theta)} d\theta \nonumber \\ &=\triangledown_{\theta} \int{q(\theta) } d\theta = \triangledown_{\theta} E_{q(\theta)} [1]=0 \nonumber \end{align}
其中1的期望$E_q(\theta) [1]=1$,而常数的导数是0。关于这里期望$E_q(\theta)$ 和求导$\triangledown_{\theta}$换位的问题,可以根据中值定理(mean value theorem)和勒贝格控制收敛定理(dominated convergence theorem)推出:
\begin{align} \triangledown_{\theta} E_{q(\theta)} [\log{q(\theta)} ] &= \lim_{\Delta \theta \to 0}{\frac{1}{\Delta \theta} (E_q [\log{q(\theta+\Delta \theta)}] - E_q [\log{q(\theta)}])} \nonumber \\ &= \lim_{\Delta \theta \to 0}{E_q [ \frac{\log{q(\theta+\Delta \theta)}-\log{q(\theta)}}{\Delta \theta}]} \nonumber \\ &= \lim_{\Delta \theta \to 0}{E_q [\triangledown_{\theta} \log{q(\Theta(\Delta \theta))} ]} \nonumber \\ &= E_q [\lim_{\Delta \theta \to 0}{\triangledown_{\theta} \log{q(\Theta (\Delta \theta))}}] \nonumber \\ &= E_q [\triangledown_{\theta} \log{q(\theta)}] \nonumber \end{align}
其中第二行到第三行运用中值定理,第三行到第四行是控制收敛定理。
分析完了式$(\ref{1.17})$的第二项,我们再来看第三项到$(\ref{1.18})$的第三项的推导:
\begin{align} \triangledown_{\theta}^2 KL(q(\theta) \parallel p(\bar{\theta} )) &= \triangledown_{\theta}^2 E_{q(\theta)} [\log{q(\theta)}] - \triangledown_{\theta}^2 E_{q(\theta)}[\log{p(\bar{\theta})} ] \nonumber \\ &= \triangledown_{\theta}^2 E_{q(\theta)} [\log{q(\theta)}] \nonumber \\ &= E_{q(\theta)} [\triangledown_{\theta}^2 \log{q(\theta)} ] \label{1.20} \end{align}
其中期望$E_{q(\theta)}$内部为对数似然(log-likelihood)的Hessian矩阵$\triangledown_{\theta}^2 \log{q(\theta)}$,它可以进行如下变换:
\begin{align} (\log{q(\theta)})'' &= ((\log{q(\theta)})' )' \nonumber \\ &= (\frac{q' (\theta)}{q(\theta)})' \nonumber \\ &= \frac{q'' (\theta)q(\theta)- q' (\theta) q' (\theta)}{q(\theta)^2} \nonumber \\ &= \frac{q'' (\theta)}{q(\theta)} - \frac{q' (\theta)}{q(\theta)} \frac{q' (\theta)}{q(\theta)} \label{1.21} \end{align}
为了好看,这里对符号做了变换,将$\triangledown_{\theta}^2$换为$(·)''$,将$\triangledown_{\theta}$换为$(·)'$。将$(\ref{1.21})$带入$(\ref{1.20})$,得到:
\begin{align} E_{q(\theta)} [\triangledown_{\theta}^2 \log{q(\theta)}] &= E_{q(\theta)} [\frac{q'' (\theta)}{q(\theta)} - \frac{q' (\theta)}{q(\theta)} \frac{q' (\theta)}{q(\theta)} ] \nonumber \\ &= E_{q(\theta)} [\frac{q'' (\theta)}{q(\theta)} ] - E_{q(\theta)} [(\log{q(\theta)} )' (\log{q(\theta) })' ] \nonumber \\ &= \int{q(\theta) \frac{q'' (\theta)}{q(\theta)}} d\theta - F \nonumber \\ &= \triangledown_{\theta}^2 \int{q(\theta)} d\theta - F \nonumber \\ &= -F \nonumber \end{align}
其中$F$为式$(\ref{1.16})$的Fisher信息矩阵,所以推出Fisher信息矩阵是KL散度的Hessian矩阵——Hessian矩阵是一个多元函数的二阶偏导(second order partial derivative)$\triangledown_{x}^2$,形式如下:
\begin{equation} H(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \dotsb & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \dotsb & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \dotsb & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \nonumber \end{equation}
经过上面的推导,最终我们得到$(\ref{1.18})$。因为$p(\bar{\theta})$是常数,我们假定它与$q(\theta)$相同,那么$(\ref{1.18})$的等号右边的第一项为0。再进一步简化$(\ref{1.18})$,得到:
\begin{equation} KL(q(\theta+\Delta \theta)\parallel p(\bar{\theta})) \approx -\frac{1}{2} \Delta \theta^T F \Delta \theta \nonumber \end{equation}
观察$(\ref{1.15})$,可以发现,此时黎曼测度张量$G(\theta)$是$-\frac{1}{2} F$。
自然梯度
标准的梯度下降法的计算采用的是式$(\ref{1.13})$,但是标准梯度下降法假设参数空间是欧式空间,而欧式空间并不适用于概率分布,所以上一节介绍了,在用KL散度来衡量分布的差异时,点$\theta$和$\theta+\Delta \theta$的距离如何表示。在上一篇我们还了解到,变分推断采用的是$ELBO$来近似地衡量变分分布与真实分布的距离——但这里我就不对$ELBO$对应的$G(\theta)$进行推导了,感兴趣的可以参考论文$[4]$——现在我们来了解如何用自然梯度(natural gradient)代替标准梯度,以及$G(\theta)$的作用。
自然梯度下降法如下所示:
\begin{align} \theta^{t+1} &= \theta^t - \eta \bar{\triangledown} L(\theta^t ) \nonumber \\ &= \theta^t - \eta G^{-1} (\theta) \triangledown L(\theta^t ) \label{1.22} \end{align}
其中$\bar{\triangledown} L(\theta^t )$是函数$L$的自然梯度,$\triangledown L(\theta^t )$是标准梯度,$\eta$是学习率,由人设定,$G^{-1}$是黎曼测度张量的逆。自然梯度$-\bar{\triangledown} L(\theta^t)$表示在黎曼空间中函数$L$的最速下降方向。对标准梯度,有:
\begin{equation} \triangledown L(\theta) = \frac{L(\theta+d \theta)-L(\theta)}{d \theta} \label{1.23} \end{equation}
其中$d\theta$表示参数$\theta$移动的距离,例如欧式距离。将$d\theta$表示为$d\theta = \varepsilon v$,其中$\varepsilon=|d\theta|$表示向量的长度,是一个很小的值——其实我们并不关心它,只关心$\theta$移动的方向——而$v$是单位向量,$|v|^2=\sum{g_{ij} v_i v_j}=v^T G(\theta)v=1$,表示$\theta$移动的方向。对$(\ref{1.23})$做一些调整:
\begin{align} &L(\theta+d\theta)= L(\theta) + \varepsilon \triangledown L(\theta)^T v \nonumber \\ &v^T G(\theta)v-1=0 \nonumber \end{align}
其中第二行为第一行的约束,约束$v$的取值范围。
最速下降法(steepest descent method)(或最速上升)是要找到方向,使函数$L$从$\theta$移动到$\theta+d\theta$时它的值下降最快,所以对$L(\theta+d\theta)$求导找到极值点:
\begin{equation} \frac{\partial L(\theta+d\theta)}{\partial v} = \frac{\partial}{\partial v} [L(\theta)+ \varepsilon \triangledown L(\theta)^T v]=0 \nonumber \end{equation}
通过拉格朗日法把对$v$的约束加入优化:
\begin{align} &\frac{\partial}{\partial v} [L(\theta)+ \varepsilon \triangledown L(\theta)^T v+ \lambda(v^T G(\theta)v-1)]=0 \nonumber \\ &0+ \varepsilon \triangledown L(\theta)^T+2 \lambda G(\theta)v-0=0 \nonumber \\ &\triangledown L(\theta)^T+2 \lambda G(\theta)v=0 \nonumber \end{align}
其中第一行等号左边第一项和最后一项与$v$无关,$v$是常数,求导后都为0;第二行的$\varepsilon$可以除掉,因为等号右边为0,左边第二项也有一个超参数$\lambda$,因此去除后无影响。结果整理,最终我们关心的最速下降(或上升)的移动方向为:
\begin{equation} v = -\frac{1}{2} \lambda G^{-1} (\theta) \triangledown L(\theta) \nonumber \end{equation}
因为$\lambda$是超参数,可以并入学习率,所以最终得到自然梯度:
\begin{equation} \bar{\triangledown} L(\theta) = G^{-1} (\theta) \triangledown L(\theta) \nonumber \end{equation}
因此得到式$(\ref{1.22})$,而且可以发现,当$G(\theta)$为单位矩阵时,自然梯度等于标准梯度。这与$(\ref{1.15})$对应,当$G(\theta)$为单位矩阵时,采用的是欧式距离。所以可以看出,标准梯度计算的也是最速下降(或上升)方向。
随机优化
了解了求自然梯度就是求标准梯度$\triangledown L(\theta)$以及$G(\theta)$后,我们来到我们的最终目标——随机自然梯度下降法。在随机梯度下降法中,我们可以只取一部分数据进行计算,此时模型的目标函数是:
\begin{equation} L(x)= \frac{1}{n} \sum_{i=1}^n{L(x_i)} \nonumber \end{equation}
其中$n$为这部分数据的数据量,$x_i$和$y_i$是第$i$个数据。目标函数的梯度为:
\begin{equation} \triangledown_{\theta} L(x) = \frac{1}{n} \sum_{i=1}^n{\triangledown_{\theta} L(x_i )} \nonumber \end{equation}
这是标准梯度,计算自然梯度我们还要通过下面的式子求$G(θ)$:
\begin{equation} G(x|\theta) = \frac{1}{n} \sum_{i=1}^n{G(x_i |\theta)} \nonumber \end{equation}
总结
变分推断这个专题总共包括三篇文章。第一篇文章介绍了变分法以及变分近似的概念,并且让我们知道,可以通过变分推断来解决那些难以计算的问题。第二篇文章以贝叶斯推断为例子,分析了为什么一些问题难以准确求解,并介绍了一种构造变分推断的方法(基于平均场定理)、变分推断的目标函数($ELBO$)以及优化算法。最后这篇介绍了随机变分推断(SVI)——通过stochastic的方法来优化变分推断模型。通过三篇文章,我们对变分推断应该是有了一个比较全面的认识。下面两篇文章,我们将来了解变分推断在变分自编码器(Variational AutoEncoder,VAE)和贝叶斯神经网络(Bayesian Neural Network,BNN)中的应用。
完结
[1] Blei, D. M., Kucukelbir, A., McAuliffe, J. D. (2018). “variational inference a review for statisticians”.
[2] Jordan, M. I., Ghahramani, Z., Jaakkola, T., and Saul, L. (1999). “Introduction to variational methods for graphical models”.
[3] Amari, S., Douglas, S. C. (1998). “why natural gradient”.
[4] Hoffman, M. D., Blei, D., Wang, C., and Paisley, J. (2013). “stochastic variational inference”.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号