引言
GAN专题介绍了GAN的原理以及一些变种,这次打算介绍另一个重要的生成模型——变分自编码器(Variational AutoEncoder,VAE)。但在介绍编码器之前,这里会先花一点时间介绍变分推断(Variational Inference,VI),而这一小系列最后还会介绍贝叶斯神经网络——其中用到了变分推断。所以,这一系列其实是一个变分推断系列。
变分推断基础
所谓推断,就是根据一定的知识或信息进行推演,然后做出某种判断。在机器学习中,无论是分类、回归还是聚类,都是推断任务。例如分类任务接收数据,然后判断它们的类别标签。类别标签或者回归任务中的回归值,又可以看成是数据的某种隐藏表征(latent representation)。这种表征可以用来描述数据,例如说“猫”的标签说明图像中有猫。实际上,神经网络中的隐藏层也可以看成是某种表征,这些表征可以是像标签一样是解耦的(disentangled)——一个个“独立”的——或者是非解耦的。
从统计概率来说,推断就是基于“条件”$x$,通过条件概率$p(y|x)$去判断某件事$y$发生的概率。但是这种从$x$到$y$的关系很多时候是未知的,或者它的解析解(analytical solution)是难以计算的——计算复杂度过高。这时候,我们就要通过一个近似解(approximate)$q$来逼近这个条件概率$p(y|x)$。
求数据分布的近似有两个重要方法[1],其中一个是马尔科夫链蒙特卡洛(Markov Chain Monto Carlo,MCMC)——MCMC是一个更传统的方法,在介绍cGAN时有提到,后面会设一个小专题详细介绍它(先挖个坑)——另一个是变分推断。变分推断和MCMC的目标都是求真实的概率密度函数(probability density)$p$的近似$q$,但MCMC是采样(sampling)的方法,而变分推断是通过优化(optimization)来求近似解。变分推断的核心思想是从变分分布的族(family)中找出其中一部分“成员”$q$,使得$q$和$p$的KL散度(Kullback-Leibler divergence)$KL(q \parallel p)$尽可能小——其实也可以取KL散度外的其他的衡量指标。KL散度的数学表示为:
\begin{equation} KL(q \parallel p) = E_q [\log{q} - \log{p} ] \label{1.1} \end{equation}
其中$E_q$表示从$q$采样,计算$\log{q} - \log{p}$的期望(expectation)$E$。当变分分布(variational distribution)$q$等于真实分布$p$时,KL散度等于0。如果用参数$\theta$来表示分布$q_{\theta}$——例如高斯分布$N(\mu,\sigma^2)$用参数均值$\mu$和方差$\sigma^2$来表示——那么变分推断就是求参数$\theta$的值或范围,使$q_{\theta}$近似$p$。这也是变分推断被“变分”推断的原因。
变分法、变分近似、变分推断
变分推断的变分来自变分法(calculus of variations)。变分又称为Frechet微分,可以理解为无限维空间上的微分。对微分(differential)来说,当我们将$x$移动$dx$时,$f(x)$会变为$f(x+dx)$。而在变分中,自变量不是点$x$,而是函数$f(x)$。当函数$f(x)$改变时,它的泛函(functional,函数的函数)$F$的输出$F(f(x))$也会发生改变。对一个函数$f$求极值(最大值maximum或最小值minimum),是在所有$x$中找到某个点,使$f(x)$取到极值;而在求一个泛函的极值时,我们是要找出$f$使泛函取到极值,例如在式$(\ref{1.1})$中,我们要找到$q$使得KL散度尽可能小。
变分近似
上面提到,因为概率密度$p(y|x)$未知或者难以计算,所以要采用近似的方法求解。论文$[2]$中,迈克尔·乔丹等人将变分推断用于概率图模型(probabilistic graphical model,或graphical model,图模型)的计算——以后会专门设一个专题系统地介绍概率图模型(第二个坑)。具体来说,迈克尔·乔丹等人通过变分近似(variational approximation),将原问题转换为简单的问题。将原问题转换为新问题的过程时,新的参数会被引入——变分参数(variational parameters)。
论文$[2]$中提到的近似方法是利用了凸共轭函数(convex conjugate function,或者称Frenchel conjugate)——在介绍f-GAN时提到过。这种变分近似的关键,在于问题的凸性(convexity)或者说凹性(concavity)——例如(图1)所示,相对于黑色直线,红色和蓝色两条曲线都只有一个极值——这一性质使得我们可以用原问题的上界(upper bound)或者下界(lower bound)来近似原问题。例如,我们可以用下面等号右边来近似对数函数(logarithm function)$\log{x}$:
\begin{equation} \log{x} = \min_{\lambda} { {\lambda x- \log{\lambda} -1} } \nonumber \end{equation}
其中$ \lambda x - \log{\lambda} - 1$是以$x$为自变量,以$\lambda$斜率的线性函数。如$(图2)$中的虚线所示,$\lambda$取不同值时,线性函数对应不同的虚线,但对确定的$x$来说,虚线上的$y$都要大于或等于对数曲线(实线)的值,也就是:
\begin{equation} \log{x} \leq \lambda x - \log{\lambda} - 1 \label{1.2} \end{equation}
变分近似就是要找出$\lambda$,使得对于某$x$$(\ref{1.2})$右边的变分函数和左边的原函数尽可能接近,而且因为右边的线性函数是一个更容易求解的函数,计算它所需的计算量显然要小于计算原函数。

(图1,来自https://www.wallstreetmojo.com)
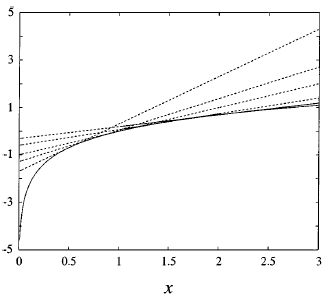
(图2,来自《an introduction to variational methods for graphical models》)
对数函数$\log{x}$,它的变分变换是$\lambda x - \log{\lambda} - 1$,那其他函数我们如何确定它们的变分变换呢?采用Frenchel共轭方法,凹函数$f$表示为:
\begin{equation} f(x) = \min_{\lambda}{{\lambda^T x - f^* (\lambda)}} \nonumber \end{equation}
$\lambda^T$是$\lambda$的向量化表示方式。$f$的共轭函数:
\begin{equation} f^* (x) = \min_x{{\lambda^T x - f(x)}} \nonumber \end{equation}
对于凸函数则有下面的共轭关系:
\begin{align} f(x) = \max_{\lambda}{{\lambda^T x - f^* (\lambda)}} \nonumber \\ f^* (x) = \max_x{{\lambda^T x - f(x)}} \nonumber \end{align}
可以发现,$\lambda^T x - f^* (\lambda)$是一个对于$x$的线性函数,而共轭函数$f^* (\lambda)$是线性函数的截距(intercept term)。但需要注意的是,凸共轭并不局限于线性边界,我们还可以用其他类型的边界,例如二次边界:
\begin{align} &f(x) = \min_{\lambda}{{\lambda^T x^2 - \bar{f}^* (\lambda)}} \nonumber \\ &\bar{f}(x)=f(x^2) \nonumber \end{align}
总之,变分推断就是用一个简单的函数去近似原问题,从而是问题能够求解。
小结
对变分推断有一个大致的概念后,现在我们梳理一下这一节的知识点,然后在下一篇介绍变分推断的目标函数以及求解过程。
变分推断要做的是根据$x$对$y$进行推断,但是因为准确推断难以计算,所以我们采用近似的办法来求解。变分近似就是一种近似方法。通过它,我们能将原问题转换为较为简单的可计算的问题。在这个转换过程中,这个方法会引入变分参数。不同的变分参数决定了函数族中函数,就像索引一样。通过变分法,我们能找出使得变分转换后的问题接近于原问题的参数,或者说函数。
[1] Blei, D. M., Kucukelbir, A., McAuliffe, J. D. (2018). “variational inference a review for statisticians”.
[2] Jordan, M. I., Ghahramani, Z., Jaakkola, T., and Saul, L. (1999). “Introduction to variational methods for graphical models”.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号