小提示1:本篇部分内容基于个人理解,仅供参考,如有错误(非常)欢迎指出。另外,如果有看不明白的不好理解的地方,也欢迎告知作者。
小提示2:转载请注明出处。
模型结构
在第三篇我们了解了InfoGan、cGAN和CycleGAN这三类GAN模型,并且我们注意到在不同的GAN中,生成器和判别器内部使用的模型各式各样。这一篇我们来看看GAN内部使用的模型,以及GAN的一些特殊的组织方式。
DCGAN
原生的GAN中,生成器和判别器采用的都是MLP(Mutli-Layer Perceptron,多层感知机)模型。鉴于CNN(Convolutional Neural Network,卷积神经网络)在图像处理上的优异表现,有不少研究者尝试在GAN中用CNN来对图像进行处理,DCGAN(Deep Convolutional GAN)就是其中的一个例子。
在DCGAN中,生成器和判别器主要是全卷积网络(all convolutional net)。在全卷积网络中,跨步卷积层(strided convolution)代替确定的空间池化层(deterministic spatial pooling,例如MaxPool)。通过跨步卷积,模型能够自己学习上采样(upsampling),而不是用人为规定的上采样方法。对于图像来说,上采样就是放大图像,增加图像分辨率。
在细节方面,DCGAN的生成器中,只有第一层采用的是全连接层(fully connected layer),生成器的最后一个卷积层直接将结果输出给判别器(DCGAN的生成器的各层结构如$图4.1$所示)。在判别器中,最后一个卷积层的输出会被展平(flatten)成一个向量,然后进入sigmoid函数,最终输出[0,1]区间的值,进行二分类判断。另外,DCGAN中除了生成器的输出层和判别器的输入层外,所有层都经过批归一化(batch normalization)。这样的处理可以使模型在深度较深时仍然有梯度。
在激活函数(activation function)的选择上,生成器的其他层采用的是ReLU函数,只有输出层是Tanh函数,因为DCGAN$[4.1]$的作者发现,采用Tanh这样的有边界(bounded)的激活函数,能让模型更快地学习数据的分布。而在判别器中,DCGAN的作者选择leaky ReLU函数,因为它在处理高分辨率的图像上更有优势。
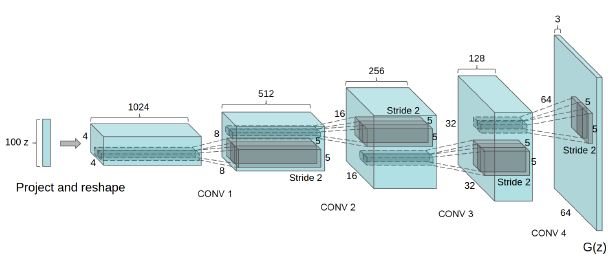
(图4.1,来自论文《Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks》)
StyleGAN
StyleGAN是一个用来处理图像的模型,它的内部结构中也包含了卷积网络。另外,StyleGAN在设计的时候借鉴风格迁移(style transfer)技术。这种技术能够让模型学到图像中的高层级(high-level)的特征——例如人像中人的姿势角度、身份特征等,而不是像素级的特征——从而实现特征解耦(feature dientanglement)。通过解耦特征,我们就能控制图像的生成。
从大的结构来说,StyleGAN的生成器可以简单地分为两个模块,其中一个是合成网络(synthesis network),另一个是特征映射(feature mapping)网络(如$图4.2$所示)。合成网络与传统的CNN类的生成器类似,也是通过卷积以及其他处理将输入转化为模拟数据。但与传统的生成器不同的是,StyleGAN中的输入不是噪音变量$z~N(0,I)$,而是一个固定的常数矩阵。另外,合成网络对它一些隐藏层有AdaIN(Adaptive Instance Normalization)操作:
\begin{equation} AdaIN(x_i,y) = y_{s,i} \frac{x_i - \mu(x_i)}{\sigma(x_i)} + y_{b,i} \label{4.1} \end{equation}
这种归一化处理方式与风格迁移中的技术相似——也和批归一化在结构上有相似之处——$(\ref{4.1})$中$x_i$是第$i$层的隐藏层(就是模型的输入数据经过i层处理后的结果),$\mu(x_i)$和$\sigma(x_i)$分别是$x_i$的均值和标准差(所以$(x_i - \mu(x_i)) / \sigma(x_i) $是归一化操作),$y$包括$y_{s,i}$和$y_{b,i}$,代表这一层需要加入的风格或者说样式,而$y_{s,i}$和$y_{b,i}$分别是平移和缩放因子,它们来自特征映射网络,也就是来自噪音变量$z$的转换。
说到特征映射模块,它主要是一个MLP模型,它的工作是将噪音变量$z$映射到解耦的特征空间$(w)$。第三篇中介绍的InfoGAN也是要实现特征解耦。InfoGAN是将噪音变量分为噪音和隐编码,然后通过训练隐编码来控制图像的表征。其实对InfoGAN、这里的StyleGAN以及其他一些模型,我们都可以将它们学习解耦表征的模块了解成编码器(encoder),只不过InfoGAN和StyleGAN不是将真实数据映射到隐空间,而是从一个隐空间映射到一个解耦的隐空间。
得到隐变量$w$后,再经过仿射变换(affine transformation),我们就得到了样式(style)$y$。仿射变换实际上就是经过全连接层处理:
\begin{equation} y=Aw+b \nonumber \end{equation}
$A$是全连接层的参数,$y$可以认为是$w$中的解耦表征的某种组合方式。为了实现$w$中特征的解耦,StyleGAN将样式$y$分别拼接(concatenate)到合成网络的不同层中,然后学习不同层的表征。为了进一步降低$w$中的特征的相关性,StyleGAN$[4.2]$的作者还采用了一种叫做混合正则化(mixing regularization)的策略。混合正则化就是用两个噪音变量$z$,每个$z$都经过特征映射生成自己的解耦特征$w$,进而生成独立的$y$。合成网络在拼接$y$时,每层都是独立地随机地选择来自第一个$z$的$y$,或者来自第二个$z$的$y$,因此在训练的时候这些$y$以及它们对应的$w$是相互独立的。
有了隐藏层$x$和样式因子$y$,StyleGAN就能生成不同风格样式的图像了。对相同的$x$和$y$,生成的图像的主体是相似的,都是人或狗,但细节上会有差别。为了控制这些细节的质量,StyleGAN的作者在合成网络中加入了额外的噪音。这些噪音是由服从高斯分布的噪音组成的单通道(single-channel)“图像”——一般的RGB图像可能有红、绿、蓝三个通道。这些“图像”以广播(broadcast)方式发送到各个卷积层的输出处,经过一个可学习的缩放参数的处理,然后与这些输出相结合(拼接)。这些随机细节可以起到例如改变头发纹路的作用。
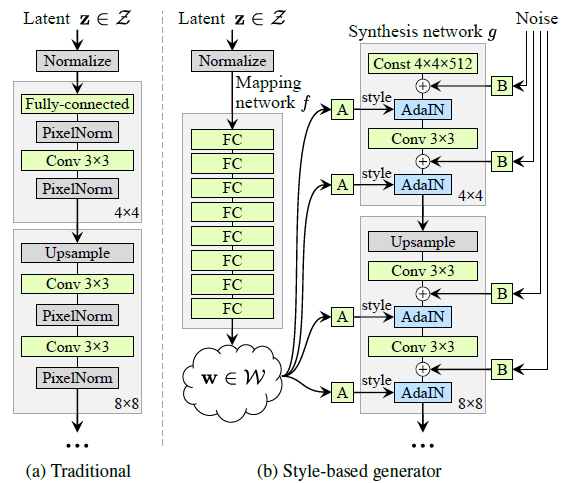
(图4.2,来自论文《A Style-based Generator Architecture for Generative Adversarial Networks》)
LAPGAN
StyleGAN是在生成器的模型的每一层进行处理,从而控制图像的不同尺度的信息。在第三篇我们介绍过一个模型$[3.4]$,它是通过设置多个生成器和判别器,来分别控制不同图像尺度的特征。通过那样的结构,模型能够处理分辨率很高的图像。这样将多个模型组织在一起的方式我们称为级联(cascade)。1983年的一篇论文$[4.3]$介绍了一种经典的图像处理的技术——拉普拉斯金字塔(Laplacian pyramid)——它采用的也是级联的结构。基于拉普拉斯金字塔,$[4.4]$的作者设计了LAPGAN。
传统的拉普拉斯金字塔是一个双向表征框架。这里的“双向”是指下采样(downsampling)和上采样(upsampling)两个的相反的过程。在下采样过程中,尺寸为$j \times j$的图像被缩小为$j/2 \times j/2$,得到一个高斯金字塔(Gaussian pyramid)。在上采样过程中,尺寸为$j \times j$的图像会被放大为$2j \times 2j$的图像。设图像为$I$,则高斯金字塔为$g(I)=[I_0,I_1,⋯,I_K]$,其中$I_0= I$,$I_K$为经过$K$次下采样后的图像。图像与其经过下采样然后再上采样得到的图像残差,也就是两个图像的差异:
\begin{align} h_k &= I_k - u(I_{k+1}) \label{4.2} \\ &= I_k - u(d(I_k)) \nonumber \end{align}
其中$h_k$为残差,$u(·)$表示上采样,$d(·)$是下采样。这些残差组成了拉普拉斯金字塔$L(h)=[h_1,h_2,⋯,h_K]$,其中最后一个残差$h_K=I_K$。如果要还原第k级的图像,我们可以采用下面的方法:
\begin{equation} I_k = h_k+ u(I_{k+1}) \end{equation}
按这样的思路,我们可以训练模型,将像素较低的图像转换为高像素的图像。
LAPGAN中每个生成器所学的,正是拉普拉斯金字塔中的残差$h_k$,所以在LAPGAN中,$k$级的图像为:
\begin{equation} I_k = G_k (z_k, u(I_{k+1})) + u(I_{k+1}) \label{4.3} \end{equation}
观察生成器$G_k$可以发现,LAPGAN是一个第三篇中介绍cGAN,$z_k$是输入到第$k$个生成器的噪音变量,$u(I_{k+1})$是cGAN的条件。LAPGAN中起始的图像,也就是分辨率最低的图像是$I_{K+1}=0$,第二级的图像是$I_K=G_K (z_K)$,其中$G_K$不是一个cGAN生成器。LAPGAN的判别器$D_k$的工作是辨别残差图像$h_k$是来自$(\ref{4.2})$还是来自$(\ref{4.3})$的$G_k$。
通过训练过的LAPGAN,我们就可以将低分辨率的图像转换为高分辨率的图(如图4.3所示)。
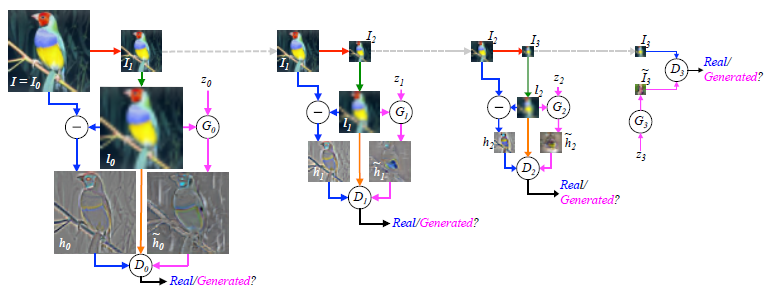
(图4.3,来自论文《Deep Generative Image Models Using a Laplacian Pyramid of Adversarial Networks》)
BigBiGAN
最后我们再来看一个比较复杂的模型,BigBiGAN。BigBiGAN借鉴了两个不同GAN模型,其中Big来自BigGAN,而Bi来自BiGAN。
BigGAN可以认为是一个内部结构更复杂的DCGAN,目前在图像生成的任务上取得了非常优异的表现。BigGAN证明了一个大容量能够一次处理大批量数据的模型能够继续提升GAN的效果。
BiGAN和第三篇中CycleGAN的部分提到过的ALI相似,也是通过编码器(encoder)学习图像的隐藏表征的模型。
BigBiGAN的基本框架延续了BiGAN(如$图4.5$),但在具体的模型上采用的是BigGAN的结构(如$图4.4$所示)。BigBiGAN在结构上对BigGAN的改动是在生成器前增加编码器(如同BiGAN),以编码器的输出作为生成器的输入。另一个改动,是像BiGAN一样,将判别器改为联合(joint)判别器。这个判别器以数据对$(x,z)$作为输入,而不是单个$x$或$z$。当$x$是真实数据$x$时,$z$就是编码器的输出$E(x)$;当$x$是生成的数据$G(z)$时,$z$是符合某个预设分布的噪音变量$z$。但相比BiGAN,BigBiGAN的目标函数中多了一元评分(unary score)项。最终,BigBiGAN的目标函数如下:
\begin{align} &V_D (P_{data},P_z) = E_{x \sim P_{data}} [l_D (x,E(x),+1)] + E_{z \sim P_z} [l_D (G(z),z,-1)] \nonumber \\[6pt] &l_D (x,z,y) = \max{(0,y {\theta}_x^T F(x))} + \max{(0,y {\theta}_z^T H(z))} + \max{(0,y {\theta}_{xz}^T J(F(x),H(z)))} \nonumber \\[6pt] &V_{EG} (P_{data},P_z ) = E_{x \sim P_{data}} [l_{EG} (x,E(x))] - E_{z \sim P_z} [l_{EG} (G(z),z)] \nonumber \\[6pt] &l_{EG} (x,z) = {\theta}_x^T F(x) + {\theta}_z^T H(z) + {\theta}_{xz}^T J(F(x),H(z)) \nonumber \end{align}
其中$V_D$和$V_{EG}$分别为判别器和生成器的目标函数,$E$为编码器,$G$为生成器,$\max{(0,·)}$为hinge函数(取括号中值最大的那个),$y$取值为+1或-1,${\theta}_x^T$、${\theta}_z^T$和${\theta}_{xz}^T$都是可学习的投射(projection),它们分别将子模型$F$、$H$、$J$输出的向量投影为数值(评分),${\theta}_x^T F(x)$和${\theta}_z^T H(z)$得到的是$x$和$z$对应的一元评分,${\theta}_{xz}^T J(F(x),H(z))$得到的是$x$和$z$的联合分数(二元评分)。另外,$F$和$H$分别是卷积网络和MLP,而$J$是以它们为输入的一个函数。通过这样的目标函数,BigBiGAN训练出来的模型,和BiGAN一样,具有循环一致性(cycle consistency),也就是$x= G(E(x))$。这和CycleGAN类似,但CycleGAN将$z$替换为真实的数据$y$。
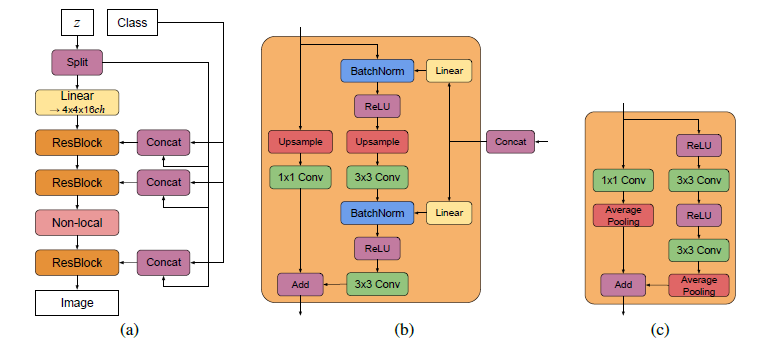
(图4.4,来自论文《Large Scale Gan Training for High Fidelity Natural Image Synthesis》)
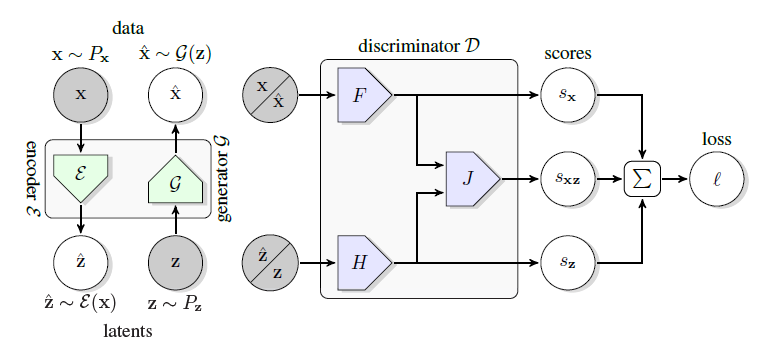
(图4.5,来自论文《Large Scale Adversarial Representation Learning》)
完结
[4.1] A. Radford, L. Metz, and S. Chintala, (2015). “Unsupervised representation learning with deep convolutional generative adversarial networks”.
[4.2] T. Karras, S. Laine, and T. Aila, (2019). “A style-based generator architecture for generative adversarial networks”.
[4.3] P. Burt and E. Adelson, (1983). “The laplacian pyramid as a compact image code”.
[4.4] E. L. Denton, S. Chintala, R. Fergus, et al., (2015). “Deep generative image models using a laplacian pyramid of adversarial networks”.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号