小提示1:本篇部分内容基于个人理解,仅供参考,如有错误(非常)欢迎指出。另外,如果有看不明白的不好理解的地方,也欢迎告知作者。
小提示2:转载请注明出处。

概述
GAN(Generative Adversarial Network,生成对抗网络)是一个网络框架,它通常包括两部分,生成器(generator)和判别器(discriminator)。生成器的作用是学习真实数据的分布(或者通俗地说就是学习真实数据的特征),然后自动地生成新的数据——所以GAN实际上是生成模型。判别器的工作是区分某个数据是真实数据,还是由生成器生成的数据。从生成器和判别器的定义可以看出,二者之间存在相互“对抗”(adversary)的关系。生成器试图生成“逼真”的数据,使判别器难以分辨,而判别器试图识别出由生成器生成的数据。生成器与判别器相互作用,目标是达到纳什均衡(Nash equilibrium)的状态。也就是说,对于判别器当前的状态,生成器达到了它的最优解,而对于生成器此时的状态,判别器也得到了最好的结果。
下面我们将从多方面去了解GAN,包括它的基础理论、学习数据的方式、它的优化案例以及一些应用案例。
基础理论
GAN及其衍生出来的模型包含了很多的数学理论,涉及微积分、概率论、线性代数等,但这里先不做太多的延申,也不是讲解基础的数学知识,而只介绍原生的GAN[1]的相关理论。
生成模型
生成模型是指通过学习数据的分布,从而模拟真实数据的模型。例如,我们假设人的身高服从高斯分布,且均值是2米,那模型就能生成一群身高在2米左右的人造人,甚至能让他们都是秃顶。已知生成模型要学习数据的分布,对于连续分布(continuous distribution),有:
$P(x) = \int{ p(x)} dx$
其中$p(·)$称为概率密度函数(probability density function)。我们以某个预设的密度函数$q(·)$或参数函数$f(·)$来模拟$p(·)$,学习数据的分布实际上是优化函数$q$的参数——例如高斯分布$N(μ,σ^2)$的参数,均值$μ$和方差$σ^2$——或f的参数,使$q$接近$p$,或$f$的输出接近于$\hat{x} \sim P(x)$。
生成模型可以分为两类,一类是显性密度模型(explicit density model),另一类是隐性密度模型(implicit density model)。显性密度模型显性地学习真实数据的分布或者分布的参数,也就是模拟出这个分布,然后用模拟的分布生成新的数据。这类模型包括最大似然模型(maximum likelihood estimator,MLE)、近似推断(approximate inference)、马尔可夫模型(Markov model)。
隐性密度模型并不需要显性的假设(explicit hypothesis),不直接学习数据的分布,而是先生成模拟数据,然后使模拟数据接近真实数据。GAN就属于隐性密度生成模型。相对于一个显性的分布,我们并不关心GAN的生成器是什么,因此它的设计所受的限制要更小。
生成器 vs 判别器
GAN中采用了生成器与判别器对抗学习的机制。生成器的操作实际上是将噪声变量/隐变量$z$(noise/latent variable)映射到模拟的数据空间$(G(z))$,其中我们自定义$z$服从某个分布$z \sim P_z (z)$,例如高斯分布$z \sim P_z (z)=N(0,I)$,而$G(·)$表示 $z$到$\hat{x}$的映射关系,也就是某个函数$f(·)$。通过这样的映射,我们就得到了生成数据$\hat{x}$,它服从分布$\hat{x} \sim P_g (\hat{x})$。真实的数据$x$服从的是分布$P_{data} (x)$。生成器的目标是使$P_g (\hat{x})$与$P_{data} (x)$接近,但我们不直接优化$P_g (\hat{x})$,而是优化$G(z)$(生成器)的参数,从而得到“逼真”的$\hat{x}$。
得到模拟数据$\hat{x}$后,GAN会让判别器$D(·)$判断数据是$\hat{x}$还是$x$。在理想状况下,对于二分类任务,$D(x)=1$而$D(\hat{x} )=0$。
目标函数
有了生成器和判别器,我们怎么训练它们呢?答案是通过目标函数。模型训练都有一个或多个目标,训练的结果是使这个或这些目标的值取到最大或最小。GAN有多种目标函数,对应不同的博弈(game)。
最大最小博弈
GAN最初的博弈采用的是最大最小博弈/零和博弈(minimax game/zero-sum game),其对应的目标函数是:
\begin{equation} \label{1.1} \min_G{\max_D{V(D,G)}} = E_{x \sim P_{data} \, (x) } [\log{D(x)} ]+ E_{z \sim P_z (z) } [\log{(1-D(G(z)))}] \end{equation}
$\min_G{\max_D{V(D,G)}}$ 表示,对于判别器$D$,训练目标是使函数$V$取到最大值,因为理想状况下,$D(x)=1$且$D(G(z))=0$,而对于生成器$G$,训练目标是最小化$V$的值。另外,$E_{x \sim P_{data} \, (x)} $表示从分布$P_{data}$中采样$x$,将样本$x$带入中括号中的函数进行计算,再求它们的均值。等号右边第一项实际上是一个似然估计(likelihood estimate),就是使D对真实数据的判断尽可能正确。
关于GAN的训练,Goodfellow在原生GAN的论文$[1]$中的建议是,每更新生成器一次后更新判别器n次,否则容易过拟合(overfitting)(例如生成的人造人都是头发都非常浓密,因为判别器没见过什么世面,错误地就认为秃顶的都是人造人)。这样1对n的优化方式,可以使在生成器更新频率相对较低时,判别器保持接近最优的状态。
对于生成器,目标函数如下:
\begin{equation} \label{1.2} \min_G{V(D^*,G)} = E_{z \sim P_z (z)} [\log{(1-D^* (G(z)))}] \end{equation}
其中$D^*$为在优化生成器时,当前最优状态的判别器,因此公式$(\ref{1.2})$式表示固定$D$,通过优化$G$使$V$的值最小。
如果我们固定生成器$G$,判别器的目标函数为:
\begin{align} \max_D{V(D,G)} &= E_{x \sim P_{data} \, (x)} [\log{D(x)}] + E_{z \sim P_z (z)} [\log{(1-D(G(z)))}] \nonumber \\ &= \int_x{p_{data}(x) \log{(D(x))}} dx + \int_z{ p_z(z) \log{(1-D(G(z)))} } dz \nonumber \\ &= \int_x{ p_{data} (x) \log{(D(x))} + p_g (x) \log{(1-D(x))}} dx \label{1.3} \end{align}
其中$p_{data} (x)$、$p_z (z)$和$p_g (x)$为概率密度函数。因为函数在极大、极小值处导数为0,所以令公式$(\ref{1.3})$关于$D(x)$的导数为0:
\begin{align} &\frac{p_{data} (x)}{D^* (x)} - \frac{p_g (x)}{(1-D^* (x))} = 0 \nonumber \\[6pt] &D^* (x) = \frac{p_{data} (x)}{(p_{data} (x) + p_g (x))} \label{1.4} \end{align}
所以最优的判别器$D^*$应该满足公式$(\ref{1.4})$。
当判别器处于最优状态时,对目标函数$(\ref{1.1})$做一些变换:
\begin{align} \min_G{V(D^*,G)} &= E_{x \sim P_{data} \, (x)} [\log{\frac{2 p_{data}(x)}{p_{data}(x) + p_g(x)}}] + E_{x \sim P_g(x)}[\log{\frac{2 p_g(x)}{p_{data}(x) + p_g(x)}}] -2 \log{2} \nonumber \\ &= \int{p_{data}(x) \log{\frac{2 p_{data}(x)}{p_{data}(x) + p_g(x)}}} dx + \int{p_g(x) \log{\frac{2 p_g(x)}{p_{data}(x) + p_g(x)}}} dx -\log{4} \nonumber \\ &= KL(p_{data} \parallel \frac{p_{data} + p_g}{2} + KL(p_g \parallel \frac{p_{data}+p_g}{2}) - \log{4} \nonumber \\ &= 2 JS(p_{data} \parallel p_g) - \log{4} \nonumber \end{align}
\begin{equation} \label{1.5} \min_G{V(D^*,G)} = 2 JS(p_{data} \parallel p_g) - \log{4} \end{equation}
其中$KL$为KL散度(Kullback-Leibler divergence),$JS$为JS散度(Jensen-Shannon divergence),它们的定义从上面的推导可知。因为$JS$的值大于等于0,当$p_{data}=p_g$时,JS散度$JS=0$,由公式$(\ref{1.5})$可知此时生成器$G$达到最优,而此时$D^* (x)=1/2$。
非饱和博弈
(图1)
(图2)
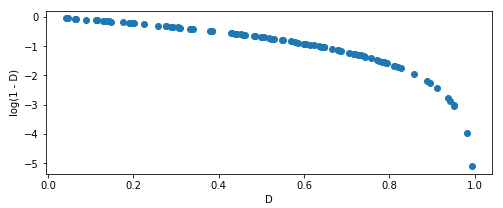
上面的推导$(\ref{1.5})$证明了零和博弈与使$p_g$逼近$p_{data}$的目标一致。但是在模型训练初期,生成器还没学会真实数据的分布,生成的数据质量较差,与真实数据有很大差别,判别器能很容易地辨别出生成的数据。在这种情况下,$D(G(z))$的值趋于零,因此$\log{(1-D(G(z)))}$的梯度(gradient)接近零(如$(图1)$中曲线的左侧非常平缓),模型趋于饱和(saturate)。因为我们在模型参数的更新时,通常采用的是梯度下降法(gradient descent):
\begin{equation} θ^{t+1} = θ^t - η \frac{∂V}{∂θ} \nonumber \end{equation}
当梯度为0时,参数θ不再更新,模型停止训练。
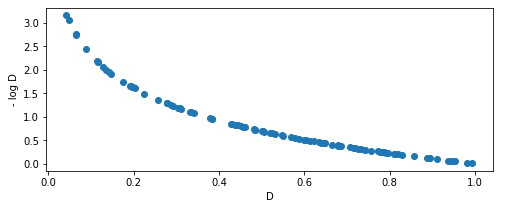
为了在训练初期能得到较大的梯度,Goodfellow在原生GAN的论文$[1]$中提出的一个方法是非饱和博弈(non-saturating game)。非饱和博弈将零和博弈中的$\log{(1-D(G(z)))}$转换为$- \log{(D(G(z)))}$。如$(图2)$所示,在训练初始阶段(曲线左侧),$D$接近0时,曲线的梯度非常大,模型没有饱和。因此,这种博弈被称为非饱和博弈。
但是非饱和博弈存在稳定性问题。根据公式$(\ref{1.5})$,对于$D^*$生成器的目标函数为:
\begin{equation} \label{1.6} E_{x \sim P_{data}(x)} [\log{D^* (x)}] + E_{x \sim P_g (x)} [\log{(1-D^* (x))}] = 2 JS(p_{data} \parallel p_g) - \log{4} \end{equation}
\begin{align} KL(p_g \parallel p_{data}) &= E_{x \sim P_g} [\log{\frac{p_g (x)}{p_data (x)}}] \nonumber \\ &= E_{x \sim P_g} [\log{\frac{p_g (x)/(p_g (x) + p_{data}(x))}{p_{data}(x)⁄(p_g(x) + p_{data}(x))}}] \nonumber \\ &= E_{x \sim P_g} [\log{\frac{(1- D^* (x))}{D^* (x)}}] \nonumber \\ &= E_{x \sim P_g} [\log{(1- D^* (x))}] - E_{x \sim P_g} [\log{D^* (x)}] \label{1.7} \end{align}
结合公式$(\ref{1.6})$和$(\ref{1.7})$:
\begin{align} E_{x \sim P_g} [- \log{D^* (x)}] &= KL(p_g \parallel p_{data}) - E_{x \sim P_g} [\log{(1- D^* (x)}] \nonumber \\ &= KL(p_g \parallel p_{data}) + E_{x \sim P_{data} \, (x)} [\log{D^* (x)}] - 2 JS(p_{data} \parallel p_g) + \log{4} \label{1.8} \end{align}
公式$(\ref{1.8})$中等号右边第一项和第二项相矛盾。第一项试图使$p_g$和$p_{data}$的KL散度尽可能小,也就是使$p_g$逼近$p_{data}$,但是第三项因为负号,试图使JS散度尽可能大,也就是让$p_g$和$p_{data}$的差异更大。
另外,非饱和博弈还有一个问题,就是会使模型趋向于生成准确度高但是多样性较差的数据,例如生成的图像虽然很逼真,但是都是一样的。导致这样的结果,是因为KL散度是不对称性(asymmetry)。观察KL散度的定义式,我们就可以发现,对于$KL(p_g \parallel p_{data})$:
当$p_g (x) \to 0$而$p_{data} (x) \rightarrow 1$,此时$p_g (x) \log{\frac{p_g (x)}{p_{data} (x)}} \rightarrow 0$,$KL$的影响趋于零;
当$p_g (x) \rightarrow 1$而$p_{data} (x) \rightarrow 0$,此时$p_g (x) \log{\frac{p_g (x)}{p_{data} (x)}} \rightarrow \infty $,$KL$的值非常大。
上面的第一种情况对应的是生成的数据多样性较差的情况,$p_g (x)$不能覆盖到所有的真实数据,在$p_{data} (x) \to 1$时$p_g (x)$却趋近于0。第二种反映的是生成的数据准确度较差的情况,在$p_{data} (x)$为0时$p_g (x)$不为零,生成了不存在的东西。$KL$的值在这两种情况下的差异,导致模型训练时第二种情况要受到更大的惩罚,因为要最小化目标函数就要使$KL$的值变小。这样,训练出来的模型就会倾向于重复地生成准确度高的安全的数据,也就是模式坍塌(mode collapse)。
最大似然博弈
除了上面两种博弈,Goodfellow在2015年的一篇论文$[2]$中还推导了另一种博弈——最大似然博弈(maximum likelihood game)。最大似然博弈与最大最小/零和博弈实际上是等价的。假设一个参数函数f,生成器的似然表示为:
\begin{align} J_G &= E_{x \sim P_g} [f(x)] \nonumber \\ &= \int{f(x) p_g (x)} dx \label{1.9} \end{align}
$J_G$关于$p_g$的参数$θ$的导数为:
\begin{equation} \frac{∂}{∂θ} J_G = \int{ f(x) \frac{∂}{∂θ} p_g (x)} dx \label{1.10} \end{equation}
假设$p_g (x) \geq 0$,那么$p_g (x) = \exp{(\log{p_g (x)})},因此式$(\ref{1.10})$变换为:
\begin{align} \frac{∂}{∂θ} J_G &= \int{f(x) \frac{∂}{∂θ} \exp{(\log{p_g (x)})}} dx \nonumber \\ &= \int{f(x) \exp{(\log{p_g (x)})} \frac{∂}{∂θ} \log{p_g (x)}} dx \nonumber \\ &= \int{f(x) p_g (x) \frac{∂}{∂θ} \log{p_g (x)}} dx \label{1.11} \end{align}
另外,KL散度的梯度为:
\begin{align} \frac{∂}{∂θ} KL(p_{data} \parallel p_g) &= \int{\frac{∂}{∂θ} p_{data} (x) \log{\frac{p_{data} (x)}{p_g (x)}}} dx \nonumber \\ &= \int{ \frac{∂}{∂θ} p_{data} (x) (\log{p_{data} (x)} - \log{p_g (x)})} dx \nonumber \\ &= \int{- p_{data} (x) \frac{∂}{∂θ} \log{p_g (x)}} dx \label{1.12} \end{align}
为了使式$(\ref{1.11})$与式$(\ref{1.12})$相等,需要:
\begin{equation} f(x) = - \frac{p_{data} (x)}{p_g (x)} \nonumber \end{equation}
当判别器最后通过sigmoid函数进行二分类判断时,即当$D(y=1\mid x) = \sigma (a(x))$时:
\begin{equation} \sigma (a(x)) = \frac{1}{(1 + exp(-a(x))} \nonumber \end{equation}
根据式$(\ref{1.4})$:
\begin{equation} D^* (x) = \frac{p_{data} (x)}{(p_{data} (x) + p_g (x))} \nonumber \end{equation}
那么:
\begin{align} \frac{p_{data} (x) + p_g (x)}{p_{data} (x)} &= \frac{1}{D^* (x)} \nonumber = \frac{1}{\sigma (a(x))} \nonumber \\[6pt] &= 1 + \exp{(-a(x))} \nonumber \end{align}
最终得到:
\begin{align} \frac{p_g (x)}{p_{data} (x)} &= - \frac{1}{f(x)} = \exp{(-a(x))} \nonumber \\[6pt] f(x) &= - \exp{(a(x))} \label{1.13} \end{align}
其中函数$a(x) = \sigma^{-1} (D(x)),\sigma^{-1}$为sigmoid函数的反函数,即logit函数:
\begin{equation} \label{1.14} \sigma^{-1}{(D)} = \log{\frac{D}{(1-D)}} \end{equation}
将式$(\ref{1.13})$和$(\ref{1.14})$带入生成器的似然$(\ref{1.9})$,得到最大似然博弈的生成器的目标函数:
\begin{align} \max_G{V(D^*,G)} &= E_{x \sim p_g} [- \exp{\log{\frac{D^* (x)}{(1-D^* (x)}}}] \nonumber \\ &= E_{z \sim p_z} [- \frac{D^* (G(z))}{(1-D^* (G(z)))}] \label{1.15} \end{align}
目标函数$(\ref{1.15})$实际上是求最大似然,因此这种博弈被称为最大似然博弈。
三种博弈方式的目标函数的曲线如$图2$所示,零和博弈和最大似然博弈在训练初期都会遇到梯度消失(gradient vanishing)的问题。
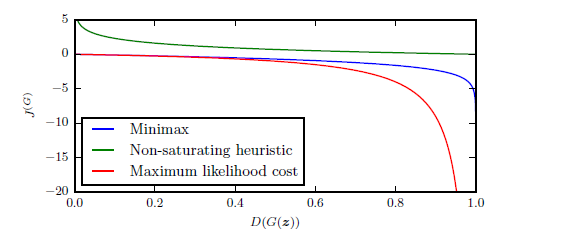
(图2,来自:论文《nips 2016 tutorial generative adversarial networks》)
未完待续~
[1] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio, (2014). “Generative adversarial nets”.
[2] I. Goodfellow, (2014). “On distinguishability criteria for estimating generative models”.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号