斯特灵数
在组合数学,Stirling数可指两类数,都是由18世纪数学家James Stirling提出的。
第一类[编辑]
第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有![s(n,k) , \left[\begin{matrix} n \\ k \end{matrix}\right]](http://upload.wikimedia.org/math/8/4/9/8494c8de074f7e71c7fbb634d3f83fd6.png) 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。
- 给定
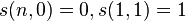 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
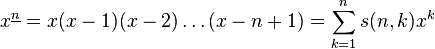
第二类
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有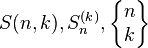 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此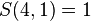 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此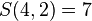 。
。
- 给定
 ,有递归关系
,有递归关系
- 递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。




 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。








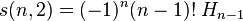
![s(n,3) = \frac{1}{2} (-1)^{n-1} (n-1)! [ (H_{n-1})^2 - H_{n-1}^{(2)} ]](http://upload.wikimedia.org/math/8/b/0/8b074a8e91fdb536ac2e87387cf3ff12.png)
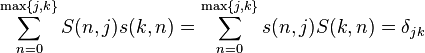
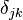 是
是
