由后序遍历结果构造二叉查找树 && 二叉查找树链表化

　　二叉查找树通俗说就是左孩子比父亲小，右孩子比父亲大。构造这么一个树，树嘛，递归即可。

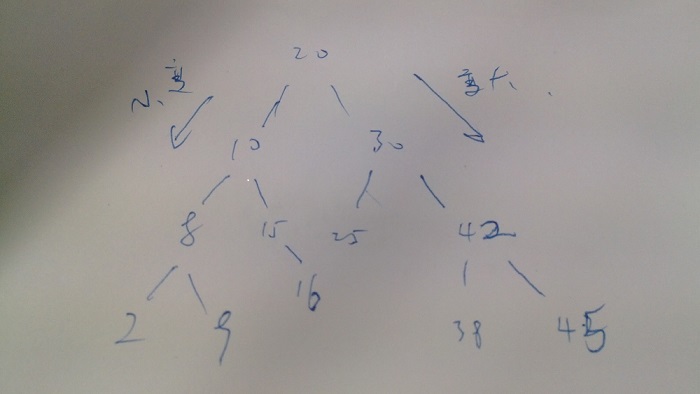
　　例如一棵树后序遍历是这样（下图的树）：2 9 8 16 15 10 25 38 45 42 30 20。最后的20肯定是树根，这里要抓住一个规律：20是树根，那么2 9 8 16 15 10都是左子树，25 38 42 45 30在右子树，因为左边都小于根、右边都大于根嘛。然后递归即可。

　　下面是树的样子和代码和src.txt（后序遍历的结果）以及运行结果：

#include <iostream>
#include <vector>
#include <fstream>

using std::cin;
using std::cout;
using std::endl;
using std::vector;

#define MY_DEBUG

struct Node
{
    int data;
    Node* pLC;
    Node* pRC;
};

Node* creatBSTree(vector<int>& arr)
{
    //数组里面没有元素
    if (!arr.size())
        return nullptr;

    Node* pNode = new Node;
    int thisData = arr.back();
    pNode->data = thisData;

    //只有一个元素就不要折腾了，它就是叶子节点，它没有左右孩子
    if (1 == arr.size())
    {
        pNode->pLC = pNode->pRC = nullptr;
        return pNode;
    }

    //下面找出左半边
    vector<int> arrLeft;
    for (int i = 0; i < arr.size() - 1; i++)
    {
        if (arr[i] < thisData)
            arrLeft.push_back(arr[i]);
        else
            break;
    }

    //下面找出右半边
    vector<int> arrRight;
    for (int i = arrLeft.size(); i < arr.size() - 1; i++)
        arrRight.push_back(arr[i]);

#ifdef MY_DEBUG
    for (int i = 0; i < arrLeft.size(); i++)
        cout << arrLeft[i] << " ";
    cout << endl;

    for (int i = 0; i < arrRight.size(); i++)
        cout << arrRight[i] << " ";
    cout << endl << endl;
#endif

    //递归处理左右孩子。arrLeft和arrRight可能为空，不要紧，在函数的开头处理了
    pNode->pLC = creatBSTree(arrLeft);
    pNode->pRC = creatBSTree(arrRight);

    return pNode;
}


//中序遍历
void show(Node* pNode)
{
    if (!pNode)
        return;

    show(pNode->pLC);
    cout << pNode->data << "  ";
    show(pNode->pRC);
}

int main(void)
{
    vector<int> arr;
    std::ifstream fin("src.txt");

    int temp;
    while (fin >> temp)
        arr.push_back(temp);

    Node* pHead = creatBSTree(arr);
    show(pHead);
    cout << endl;
    cin.get();
}

2 9 8 16 15 10 25 38 45 42 30 20

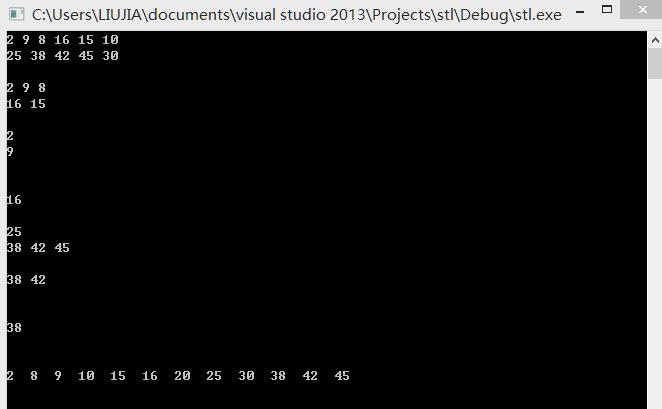
　　由其他的遍历方式得到树的道理类似。

---

---

---

 

题目：

　　输入一个整数数组，判断该数组是不是某二元查找树的后序遍历的结果。如果是返回true，否则返回false。

分析：

　　这不是很简单了嘛，由最后的根把输入分成三份，第一份是左孩子，第二份是右孩子，最后是树根。7、4、6、5就不能构成了，因为5是根，那么7,4,6都是右子树里面的，但是里面有小于5的4，所以不行。递归即可。

---

---

---

 

题目：

　　输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。要求不能创建任何新的结点，只调整指针的指向。

　　例如如果树如上图，那么得到的链表是 2=8=9=……=42=45。

分析：

　　树嘛，递归就是啦。

　　如上树，先递归处理左子树（根为10的树），处理完左子树就成了一个链表了，并要能够返回左子树的最大节点16；然后递归处理右子树（根为30的树），处理完右子树也成了一个有序链表，并返回右子树的最小节点25，然后把16、20、25串起来，不就是链表了嘛？

　　这里要注意一点：在处理根为20的树时，这是不是要递归处理根为10的左子树嘛，那么这个左子树怎么知道它要返回16节点呢？同样对于20的右子树，它怎么知道返回25以和20串起来呢？所以在处理子树的时候，要传给它一个标志，表明它是父亲的左子树还是右子树。我在这里纠结好久……

代码：

#include <iostream>
#include <set>
#include <fstream>
#include <queue>

using std::cin;
using std::cout;
using std::endl;
using std::set;
using std::vector;

struct Node
{
    int data;
    Node* pLC;
    Node* pRC;
};

Node* creatBSTree(vector<int>& arr)
{
    //数组里面没有元素
    if (!arr.size())
        return nullptr;

    Node* pNode = new Node;
    int thisData = arr.back();
    pNode->data = thisData;

    //只有一个元素就不要折腾了，它就是叶子节点，它没有左右孩子
    if (1 == arr.size())
    {
        pNode->pLC = pNode->pRC = nullptr;
        return pNode;
    }

    //下面找出左半边
    vector<int> arrLeft;
    for (int i = 0; i < arr.size() - 1; i++)
    {
        if (arr[i] < thisData)
            arrLeft.push_back(arr[i]);
        else
            break;
    }

    //下面找出右半边
    vector<int> arrRight;
    for (int i = arrLeft.size(); i < arr.size() - 1; i++)
        arrRight.push_back(arr[i]);

#ifdef MY_DEBUG
    for (int i = 0; i < arrLeft.size(); i++)
        cout << arrLeft[i] << " ";
    cout << endl;

    for (int i = 0; i < arrRight.size(); i++)
        cout << arrRight[i] << " ";
    cout << endl << endl;
#endif

    //递归处理左右孩子。arrLeft和arrRight可能为空，不要紧，在函数的开头处理了
    pNode->pLC = creatBSTree(arrLeft);
    pNode->pRC = creatBSTree(arrRight);

    return pNode;
}

//中序遍历
void show(Node* pNode)
{
    if (!pNode)
        return;

    show(pNode->pLC);
    cout << pNode->data << " ";
    show(pNode->pRC);
}

//这个函数多传了一个参数 asLeft，表明树根是树根的左子树还是右子树
//因为如果是左子树的话，那么要返回左子树最大节点，右子树要返回最小节点
//不要这个标志的话 pNode 不知道指向的树到底是父亲的左子树还是右子树
Node* letStraight(Node* pNode, bool asLeft)
{
    //如果是空树或者只是一个叶子节点，返回自身
    if (!pNode || (!pNode->pLC && !pNode->pRC))
        return pNode;

    //递归处理左右子树
    Node* pLMax = nullptr;
    if (pNode->pLC)
        pLMax = letStraight(pNode->pLC, true);

    Node* pRMin = nullptr;
    if (pNode->pRC)
        pRMin = letStraight(pNode->pRC, false);

    //连接左子树、右子树、树根
    if (pLMax)
    {
        pNode->pLC = pLMax;
        pLMax->pRC = pNode;
    }
    if (pRMin)
    {
        pNode->pRC = pRMin;
        pRMin->pLC = pNode;
    }

    //返回值处理，注意 asLeft 表明这棵树是它父亲的左子树还是右子树，所以它要重新找到合适的返回节点
    // pNode 的左孩子最大或右孩子最小并不是它要返回的值，它要返回的还是要看这整棵树，而不是单单看左右孩子
    Node* pRetutnNode = pNode;
    if (asLeft)
    {
        while (pRetutnNode->pRC)
            pRetutnNode = pRetutnNode->pRC;
    } 
    else
    {
        while (pRetutnNode->pLC)
            pRetutnNode = pRetutnNode->pLC;
    }
    return pRetutnNode;
}

int main(void)
{
    vector<int> arr;
    std::ifstream fin("src.txt");

    int temp;
    while (fin >> temp)
        arr.push_back(temp);

    Node* pHead = creatBSTree(arr);
    show(pHead);
    cout << endl;

    //顺序链表化并返回第一个节点
    pHead = letStraight(pHead, false);
    while (pHead)
    {
        cout << pHead->data << " ";
        pHead = pHead->pRC;
    }
    cout << endl;

    cin.get();
}

结果：