动态规划和分治法有点相似---通过组合子问题的解来求解原问题.
分治法将问题分解为互不相交的子问题,递归地求解子问题,再将它们的解合并起来得到原问题的解.
动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题是递归求解的,将其划分为更小的子问题),这种情况下分治算法会做许多重复的工作,即反复求解公共的子问题,动态规划就是要对每个子问题求解一次,将其保存在一个表格中,从而无需每次求解一个子问题都重新计算.
通常按下面4个步骤设计一个动态规划算法:
1:刻画一个最优解的结构特征;
2:递归地定义最优解的值;
3:计算最优解的值(可以采用自底向上或自顶向下的方法)
4:利用计算的值构造一个最优解
最优子结构性质:问题的最优解有相关子问题的最优解组合而成,而这些子问题可以独立求解
&&:钢条切割
长度为n(正整数)的钢条,给定每种长度的价格,现把钢条切割,随你切,但切的每一段长度都是整数,卖,卖最多的钱(切割不计费),下面是长度对应的价钱
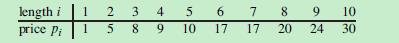
现在对任意的n,求卖的最多钱.
长度为n的钢条共有2^(n-1)中切割方案,即共有n-1个可以切割的点,每个点有两个状态:切,不切.这里没考虑对称的情况. 用Rn(n>=1)表示长为n的钢条卖的最多钱,则可以用更短的钢条的最优切割收益来描述它,这叫最优子结构性质 ![]() 即Rn是整个没切割的和其他n-1种切割方法(+表示切后的长度)获益中最大值.
即Rn是整个没切割的和其他n-1种切割方法(+表示切后的长度)获益中最大值.
将上面的递归式简化:将钢条从左端切下长为i的一段,只对剩下的n-i继续切割,这样还解决了不切的情况,则![]() (即n种情况) , 这个递归式求解为:
(即n种情况) , 这个递归式求解为:
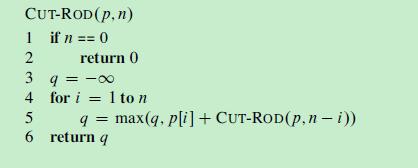
(见<算法导论>P206,可以把p去掉)
这是上面递归的代码,结果正确,但效率低

#include <stdio.h> const int p[11]={0,1,5,8,9,10,17,17,20,24,30}; int Cut_Rod(int n) //对于长度为n的 { if (!n) { return 0; } int q=-1; for (int i=1;i<=n;i++) //对左边的长 { int qtemp=p[i]+Cut_Rod(n-i); if (qtemp>q) { q=qtemp; } } return q; } int main(void) { int t; while (scanf_s("%d",&t)!=EOF) { printf("%d\n",Cut_Rod(t)); } getchar(); return 0; }
这是动态规划,自顶向下的代码,即记录了已经算过的值

#include <stdio.h> #include <string.h> const int p[11]={0,1,5,8,9,10,17,17,20,24,30}; //价格表 int r[101]; //假设最长为100 int Memoized_Cut_Rod_Aux(int n) //这个函数是正式算的,自顶向下 { if (r[n]>=0) { return r[n]; } int q=-1; if (n==0) { q=0; } else { for (int i=1;i<=n;i++) { int qtemp=p[i]+Memoized_Cut_Rod_Aux(n-i); if (qtemp>q) { q=qtemp; } } } r[n]=q; return q; } int Memoized_Cut_Rod(int n) //对于长度为n的 { memset(r,-1,sizeof(r)); //置为-1 return Memoized_Cut_Rod_Aux(n); } int main(void) { int t; while (scanf_s("%d",&t)!=EOF) { printf("%d\n",Memoized_Cut_Rod(t)); } getchar(); return 0; }
感觉这里的动态规划其实就是对递归低效的改进...
&&:矩阵链相乘
求最少的相乘次数.A1A2A3A4...An个矩阵相乘,用动态规划,就是选一个k, 1<=k<n 把矩阵链分为 (A1...Ak)和(Ak+1...An),使得左边的链次数加上右边的链次数再加上最后的两个相乘次数最少的就行了,然后再递归.学到
1:用二维数组保存从链 (i,i+1,...j)的最少次数,即 CS[i][j] ,用二维数组保存链 (i,i+1,...j)的分割点,即 FG[i][j]---二维数组可以干很多事啊!
2:递归地显示最后的结果

/*动态规划---矩阵链相乘*/ #include <stdio.h> #include <string.h> #include <limits.h> int matrix[12]={5,2,3,5,12,6,4,99,7,4,17,3}; //给定11个矩阵,每个矩阵为 i*(i+1) 0<=i<=10 int MinTimes[12][12]; //这个数组保存从第一个下标到第二个下标的矩阵链的最少乘次数,则结果就在 MinTimes[1][11]中,注意下标 int Record[12][12]; //记录是怎么切分的,记录从下标是前一个到后一个切分点,切分点>=1 int Min_Times(int i,int j) //从矩阵i,到j的最少次数, 1<=i<=12, 1<=j<=11 { /*自顶向下*/ if (i==j) //只有一个矩阵,不需要做两个矩阵的相乘 { return 0; } else { if (!MinTimes[i][j]) //如果还没计算出来 { MinTimes[i][j]=INT_MAX; //先把它置为很大 for (int k=i;k<j;k++) //对于k的每种情况,注意k的范围, i<=k<j 一定是会被切分的,因为按顺序来的话也是切分啊---在最后一个之前切分的! { int temp=Min_Times(i,k)+Min_Times(k+1,j)+matrix[i-1]*matrix[k]*matrix[j]; if (temp<MinTimes[i][j]) { MinTimes[i][j]=temp; Record[i][j]=k; //记录 } } } return MinTimes[i][j]; } } int Get_Min_Times() { /*先初始化数组*/ memset(MinTimes,0,sizeof(MinTimes)); //先全部置为0 memset(Record,0,sizeof(Record)); //置为0 return Min_Times(1,11); //调用的时候 } void Show(int i,int j) //显示从i,到j是怎么划分的 { if (i==j) { printf("A%d",i); } else { putchar('('); Show(i,Record[i][j]); Show(Record[i][j]+1,j); putchar(')'); } } int main(void) { printf("%d \n",Get_Min_Times()); Show(1,11); getchar(); return 0; }
&&:最长子序列
两个数组,求最长子序列,子序列---即第一个数组从前至后任选几项,这几项从前至后依次能在第二个数组中找到
动态规划:m[i][j]表示最长的个数,i指向数组X,j指向Y,从X和Y的最后一项出发,若最后一项相等,则m[i][j]=m[i-1][j-1]+1;否则为m[i-1][j]和m[i][j-1]的最大值,注意边界.
学到:
1:逗号表达式的值为最后一项的值;
2:它的输出方式,用一维数组出错,用二维数组,并且还要看方向,根据方向看能不能输出

/*动态规划---最长公共子序列*/ #include <stdio.h> #include <string.h> #define MAXLEN 101 //最多100个字符 char x[MAXLEN],y[MAXLEN]; int m[MAXLEN][MAXLEN]; //m[i][j]表示x的从i下标一直到开始和y从j下标一直到开始的两段的最长公共子序列的字符个数, //则结果即为m[len_x-1][len_y-1],下标从0开始 int record[MAXLEN][MAXLEN]; //用二维数据记录,一维的不行.... 1--可以输出,即 ↖,2--←,3--↑ int MaxLen(int i,int j) //真正开始,这里为自顶向下---我喜欢 { if (i==-1||j==-1) //递归的边界 { return 0; //表示没有 } else { if (!m[i][j]) //没计算过 { if (x[i]==y[j]) //指向的最后一个相等 { m[i][j]=MaxLen(i-1,j-1)+1; record[i][j]=1; //表示这个是可以输出的,记录这个 } else //指向的最后一个不相等,则为两种情况的的最大值 { int len1=MaxLen(i-1,j); if (i>=1) { m[i-1][j]=len1; //能记录的就记录 } int len2=MaxLen(i,j-1); if (j>=1) { m[i][j-1]=len2; } m[i][j]=len1>len2?(record[i][j]=2,len1):(record[i][j]=3,len2); //逗号表达式返回第二个值! } } return m[i][j]; } } int Get_MaxLen(int i,int j) //真正开始的前奏,注意这里传进来的为可以找到字符的下标 { /*先初始化*/ memset(m,0,sizeof(m)); memset(record,0,sizeof(record)); //是的,则为1; return MaxLen(i,j); } void Show(int i,int j) //得传进来在两个数组的下标 { if (i==-1||j==-1) { return; } else if(record[i][j]==1) { Show(i-1,j-1); //逆序 printf("%c ",x[i]); } else if(record[i][j]==2) { Show(i-1,j); } else { Show(i,j-1); } } int main(void) { while (gets(x)&&gets(y)) //有点不安全啊 { int len_x=strlen(x); int len_y=strlen(y); printf("%d\n",Get_MaxLen(len_x-1,len_y-1)); Show(len_x-1,len_y-1); putchar('\n'); } getchar(); return 0; }
&&:最优二叉搜索树
最优二叉搜索树,首先是二叉搜索树,非正式解释:对于根节点,左子树中所有节点值小于根节点,右子树中所有节点的值大于根节点,递归一下就行了.
最优二叉搜索树,则要使从根节点开始搜索,直到有了搜索结果的期望最小.
给定一个已经排好了序的待构造的数组,建这样的树.用动态规划的思想:每次让数组中一个凸出来(因为数组可以看成平的)作为树根,递归构造左右子树,算权值,选出权值最小的即可,满足最优子结构和子问题重叠. 这里和书<算法导论>不太一样,我假设每次搜索都是成功的.

/*动态规划---最优二叉搜索树*/ #include <stdio.h> #include <limits.h> #include <string.h> #define MAXLEN 10 //假设最多的待构造的节点数 char elem[MAXLEN]={'a','b','c','d','e','f','g','h','i','j'}; //给定了已排序的元素 int weight[MAXLEN]={5,7,2,8,9,3,1,4,6,2}; //各个权值 int m[MAXLEN][MAXLEN]; //m[i][j]表示下标从i到j的最优二叉搜索树的总期望,则结果为m[0][9] int w[MAXLEN][MAXLEN]; //w[i][j]表示下标从i到j的树的权值和 int record[MAXLEN][MAXLEN]; //record[i][j]记录下标从i到j所选的树根 int Min(int i,int j) //正式干活的函数 { if (j==i-1) //递归边界,即是空树,这样弄其实更为了不让数组越界 { return 0; } else { if (!m[i][j]) //即这还没有算过 { m[i][j]=INT_MAX; for (int k=i;k<=j;k++) { int m1=Min(i,k-1); //暂存,怕数组越界 if (i!=k) { m[i][k-1]=m1; //避免重复算同样的问题 } int m2=Min(k+1,j); if (k!=j) { m[k+1][j]=m2; } int temp=m1+m2+w[i][j]; if (temp<m[i][j]) { m[i][j]=temp; record[i][j]=k; } } } return m[i][j]; } } int Get_Min(int i,int j) //前奏函数 { /*先初始化*/ memset(m,0,sizeof(m)); //初始化为无穷大 memset(record,-1,sizeof(record)); for (int k=0;k<MAXLEN;k++) //初始化w[][] { for (int t=k;t<MAXLEN;t++) { w[k][t]=0; for (int v=k;v<=t;v++) { w[k][t]+=weight[v]; } } } return Min(i,j); } void Show(int i,int j) { if (j==i-1) //递归边界 { return; } else { putchar('('); Show(i,record[i][j]-1); //先显示左树 printf(" -%c- ",elem[record[i][j]]); //显示根 Show(record[i][j]+1,j); //显示右树 putchar(')'); } } int main(void) { printf("%d\n",Get_Min(0,9)); Show(0,9); /* for (int k=0;k<MAXLEN;k++) //初始化w[][] { for (int t=k;t<MAXLEN;t++) { printf("%d ",m[k][t]); } putchar('\n'); } */ getchar(); }
&&:最长矩形包含链
给你一些矩形,定义一个矩形(a,b)能包含另一个矩形(c,d)就是矩形的边的长满足a>c且b>d或者a>d且b>c.非官方就是一个矩形能把另一个套住嘛.然后求一个矩形包含链,这个链中除了最后一个,后面的矩形都能包含前面的矩形,求最长的包含链.
为什么是动态规划问题呢?一个矩形能包含另一个矩形就是二元关系嘛,二元关系可以用图来表示嘛,每个矩形是一个结点,一个能包含另一个就是这两个结点之间有一条有向弧嘛,其实问题转化成了求这个图的最长路径!
动态规划的思想是我一下子会写图最长路径的算法了,比起书上的什么难写的.《算法导论》真是好书啊!

#include <stdio.h> #define MAXNUM 10 //最多矩形个数 typedef struct //矩形结构体 { int x; int y; }Rectangle; Rectangle ArrRect[MAXNUM]={{3,4},{2,5},{7,8},{8,2},{10,5},{4,9},{5,8},{5,9},{13,17},{11,12}}; //这么多矩形 char ArrRectName[MAXNUM]; //对应矩形的名字 int relation[MAXNUM][MAXNUM]; //用邻接矩阵表示图的各个顶点的关系 int m[MAXNUM]; //表示从各个顶点出发能到的最长距离 int aft[MAXNUM]; //记录,只要记住每顶点后面的一个就行了,要记录从各个顶点出发的情况 int Get_Max(int n) //正式干活了,传进顶点的下标---其实这里是自顶向下,更容易理解 { /*对n能到的所有顶点*/ for (int i=0;i<MAXNUM;i++) { if (relation[n][i]) //从n能到达i顶点 { if ((m[i]==1)) //i顶点的最大距离还没有算好了 { m[i]=Get_Max(i); //先算从i出发能到的最大距离---记忆化 } if (m[i]+1>m[n]) //+1大于当前m[n] { m[n]=m[i]+1; aft[n]=i; //最长距离的话,n的后继就是i了 } } } return m[n]; //返回距离 } void Prelude(void) //前奏 { /*初始化矩形名字*/ for (int i=0;i<MAXNUM;i++) { ArrRectName[i]='a'+i; } /*初始化图关系*/ for (int i=0;i<MAXNUM;i++) { for (int j=0;j<MAXNUM;j++) { if (i!=j) { if ((ArrRect[i].x<ArrRect[j].x&&ArrRect[i].y<ArrRect[j].y)||(ArrRect[i].x<ArrRect[j].y&&ArrRect[i].y<ArrRect[j].x)) { relation[i][j]=1; } else { relation[i][j]=0; } } else //自己到自己,没关系 { relation[i][j]=0; } } } /*初始化距离*/ for (int i=0;i<MAXNUM;i++) { m[i]=1; //初始化为1,因为不能到任何顶点的情况下只有它一个,为1 } /*初始化记录表*/ for (int i=0;i<MAXNUM;i++) { aft[i]=-1; //假定没有后继 } /*求各个顶点出发的最大距离*/ for (int i=0;i<MAXNUM;i++) { m[i]=Get_Max(i); } } void Show(void) { /*图关系矩阵*/ puts("图关系矩阵"); for (int i=0;i<MAXNUM;i++) { for (int j=0;j<MAXNUM;j++) { printf("%d ",relation[i][j]); } putchar('\n'); } /*各个顶点能到的最大距离*/ puts("各个顶点能到的最大距离"); for (int i=0;i<MAXNUM;i++) { printf("%d ",m[i]); } putchar('\n'); /*显示从各个顶点出发的最长路径*/ puts("显示从各个顶点出发的最长路径"); for (int i=0;i<MAXNUM;i++) { int temp=i; //暂时记录i printf("%c ",ArrRectName[i]); //不管有没有后面的先输出自己 while (aft[temp]!=-1) { printf("%c ",ArrRectName[aft[temp]]); temp=aft[temp]; //temp指向后面的 } putchar('\n'); } } int main(void) { Prelude(); Show(); getchar(); return 0; }
uva oj上面的一题,就是给定几个历史事件的正确排序,然后学生将这几个事件排序,代码的目的是给学生排序评分,这里是只要找到学生提交的排序中最长的子序列(不一定要连续)即可.注意它的输入比较奇葩...害我晚上搞了好长时间结果出错,虽然思路是正确的......
显然是动态规划的思想:把每个历史事件看做图的一个顶点,则正确的排序可以用一条从第一个一直到最后一个的线连起来,也就是最长路径嘛!你要做的就是从任一点出发,连线,找到从这一点出发所能到达的最长长度,然后比较从所有点出发的最长,得出结果.而图的连通性则是根据给定的正确顺序得到.其实和上面一题的思路一样.

#include <stdio.h> #include <string.h> int src[21]; //原来的,0号单元不用最多为1,2,...20 int srctemp[21]; //我去!英语不是很厉害啊!理解错了.... int ans[21]; //学生的答案,0号单元不用最多为1,2,...20 int anstemp[21]; //待转换 int m[21]; //从学生的答案的各个数出发能到达的最大值,最后的结果就是这个数组红的最大值 int vis[21]; //表示是否算过 int relation[21][21]; //关系图,用矩阵表示,0号单元同样不用 int N; //数字的多少 int MaxLen(int p) //正式计算从下标为i开始的最大距离 { if (!vis[p]) //ans[]中下标为盘的没有计算过,这才算,否则直接返回 { for (int i=p+1;i<=N;i++) //从它本身开始的ans[]数组的后面所有 { if (relation[ans[p]][ans[i]]) //能到,即数字ans[p]在ans[i]前面 { m[i]=MaxLen(i); //自顶向下,并记录 vis[i]=1; //算过 if (m[i]+1>m[p]) { m[p]=m[i]+1; } } } } return m[p]; } void Inite(void) //初始化 { /*初始化是否算过,初始化结果的数组,注意初始化为1*/ for (int i=1;i<=N;i++) { m[i]=1; vis[i]=0; //默认没算过 } /*初始化关系*/ memset(relation,0,sizeof(relation)); for (int i=1;i<=N;i++) { for (int j=i+1;j<=N;j++) { relation[src[i]][src[j]]=1; //注意这里的关系下标就是那个数 } } /*计算每个开始的最大距离*/ for (int i=1;i<=N;i++) { m[i]=MaxLen(i); } } int main(void) { scanf("%d",&N); /*读原始数据*/ for (int i=1;i<=N;i++) //注意从1开始 { scanf("%d",&srctemp[i]); } /*对原始数据进行转换*/ for (int i=1;i<=N;i++) { src[srctemp[i]]=i; } /*下面读不确定多少的情况*/ while (scanf("%d",&anstemp[1])!=EOF) //直接读第一个 { for (int i=2;i<=N;i++) { scanf("%d",&anstemp[i]); } /*转换学生的数字*/ for (int i=1;i<=N;i++) { ans[anstemp[i]]=i; } /*计算这个情况*/ Inite(); int max=0; for (int i=0;i<=N;i++) { if (m[i]>max) { max=m[i]; } } printf("%d\n",max); } return 0; }





