【总结】二叉堆

简单介绍

最小堆：最小堆是一个关键码序列{K1,K2,…,Kn}，它具有如下特性：

K[i] <= K[2i]

K[i] <= K[2i+1]

类似可以定义最大堆。

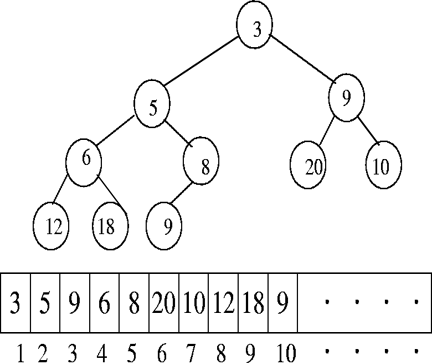
性质

完全二叉树的层次序列，可以用数组表示。

堆中储存的数是局部有序的，堆不唯一。

​ 节点的值与其孩子的值之间存在限制。

​ 任何一个节点与其兄弟之间都没有直接的限制。

从逻辑角度看，堆实际上是一种树形结构。

基本操作

top

直接返回根结点

时间复杂度O(1)

pop

弹出当前的最小值

删掉根节点将最下面的节点放到根节点的位置

再把根节点下传

void pop()
{
	cout << "pop" << endl;
	heap[1] = heap[n]; n--; downdate(1); //直接删除堆顶，把最后一个元素放到堆顶，下滤 
	//print();
}
void downdate(int x){
	while(x*2<=n){
		int y=x*2;
		if(x*2<n&&heap[x*2+1]<heap[x*2]){
			y=x*2+1;
		}
		if(heap[x]<=heap[y])break;
		swap(heap[x],heap[y]);
		x=y;
	}
} 

push

插入一个数

插入到后的位置，与它的父亲节点比较，进行上传

void insert(int x){
	heap[++n]=x;
	update(n);

}
void update(int x){//上滤操作qwq 
	while(x!=1){
		if(heap[x/2]<=heap[x])break;
		swap(heap[x/2],heap[x]);
		x/=2;
	}
}

stl

priority_queue相当于一个堆,其实平时用的比较多的也是stl中的堆emm

定义：priority_queue a;

插入队尾：a.push(x);

删除队首：a.pop();

查询队首：a.top();

清空只能慢慢pop。

例题：序列合并

详细解释看题解：传送门

分析

固定 A[i], 每 n 个和都是有序的：

A[1] + B[1] <= A[1] + B[2] <= … <= A[1] + B[n]

A[2] + B[1] <= A[2] + B[2] <= … <= A[2] + B[n]

…

A[n] + B[1] <= A[n] + B[2] <= … <= A[n] + B[n]

每次只需要考虑第一行第一个还未考虑的数即可

例题：丑数

丑数是指质因子在集合 {2, 3, 5, 7} 内的整数，第一个丑数是 1.

现在输入 n，输出第 n 大的丑数。

n <= 10000.

分析

与上一个题是非常非常相似的，唯一的不同在与上一个题是二元组，而我们现在考虑的是一个四元组

用四元组(a, b, c, d)表示 2a3b5c7d，1就是 (0, 0, 0, 0)

用最小堆存 2a3b5c7d ，每次取出最小值 (a, b, c, d)。

然后把 (a + 1, b, c, d) (a, b + 1, c, d) (a, b, c + 1, d) (a, b, c, d + 1) 插入堆中。

注意堆顶元素如果和上一个输出的数相等就需要 pop 掉。