Codeforces 703C（计算几何）

C. Chris and Road

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

And while Mishka is enjoying her trip...

Chris is a little brown bear. No one knows, where and when he met Mishka, but for a long time they are together (excluding her current trip). However, best friends are important too. John is Chris' best friend.

Once walking with his friend, John gave Chris the following problem:

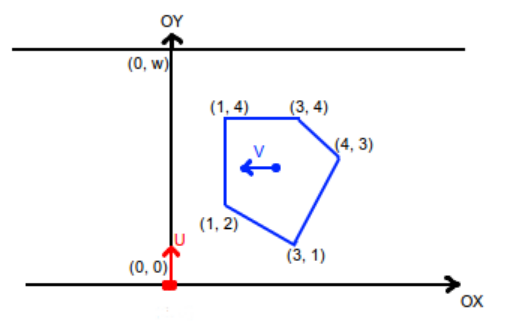
At the infinite horizontal road of width w, bounded by linesy = 0 and y = w, there is a bus moving, presented as a convex polygon ofn vertices. The bus moves continuously with a constant speed ofv in a straight Ox line in direction of decreasingx coordinates, thus in time only x coordinates of its points are changing. Formally, after timet each of x coordinates of its points will be decreased byvt.

There is a pedestrian in the point (0, 0), who can move only by a vertical pedestrian crossing, presented as a segment connecting points(0, 0) and (0, w)with any speed not exceedingu. Thus the pedestrian can move only in a straight lineOy in any direction with any speed not exceedingu and not leaving the road borders. The pedestrian can instantly change his speed, thus, for example, he can stop instantly.

Please look at the sample note picture for better understanding.

We consider the pedestrian is hit by the bus, if at any moment the point he is located in liesstrictly inside the bus polygon (this means that if the point lies on the polygon vertex or on its edge, the pedestrian is not hit by the bus).

You are given the bus position at the moment 0. Please help Chris determine minimum amount of time the pedestrian needs to cross the road and reach the point(0, w) and not to be hit by the bus.

Input

The first line of the input contains four integers n,w, v,u (3 ≤ n ≤ 10 000,1 ≤ w ≤ 10⁹,1 ≤ v,  u ≤ 1000) — the number of the bus polygon vertices, road width, bus speed and pedestrian speed respectively.

The next n lines describes polygon vertices in counter-clockwise order.i-th of them contains pair of integers x_i and y_i ( - 10⁹ ≤ x_i ≤ 10⁹,0 ≤ y_i ≤ w) — coordinates ofi-th polygon point. It is guaranteed that the polygon is non-degenerate.

Output

Print the single real t — the time the pedestrian needs to croos the road and not to be hit by the bus. The answer is considered correct if its relative or absolute error doesn't exceed10^- 6.

Example

Input

5 5 1 2
1 2
3 1
4 3
3 4
1 4

Output

5.0000000000

Note

Following image describes initial position in the first sample case:

 

题目大意：

    人从原点出发，可以以小于等于u的任意速度向上或向下运动，一个n边型的车以恒定的速度v向左运动（竟然有车长得这么奇葩），给出车各个点的初始坐标。求人在不被车撞的前提下最快到达对面的时间。

 

解题思路：

    一共有两种情况。

    第一种情况、人开始就一直以u的速度往前走，没有被车撞。那么时间最短就是w/u。

    第二种情况，人要在车后面过去。那么为了时间最短人一定要安全的前提下尽量贴着车走才能时间最短。

    我们可以将问题看成车不动，人先水平移动一段距离，再沿着斜率为u/v的直线运动。那么就变成了平移直线使其与车相切。由于车的每条边都是直线，那么切点一定在顶点上。我们只要枚举全部顶点，一个点和一个斜率就可以确定一条直线。我们只要找到最左边和最右边一条直线则这两条直线与车一定是相切的。这时切线与x轴交点如果在原点左边，那么就是第一种情况。否则是第二种情况。在我们新建的模型下时间就非常好求。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<map>
#include<set>
#include<queue>
using namespace std;
int n,w,v,u;
int main()
{
    scanf("%d%d%d%d",&n,&w,&v,&u);
    double k=u*1.0/v,l=(double)(1<<30)-1,r=0;
    int i;
    //cout<<l<<endl;
    for (i=1;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        l=min(l,x-y/k);
        r=max(r,x-y/k);
    }
    printf("%.10lf\n",l>0?w*1.0/u:r/v+w*1.0/u);
    return 0;
}