整理自:
https://blog.csdn.net/woaidapaopao/article/details/77806273?locationnum=9&fps=1
- 公式推导
- 逻辑回归的基本概念
- L1-norm和L2-norm
- LR和SVM对比
- LR和随机森林区别
- 常用的优化算法
1.公式推导(必会)
2.逻辑回归的基本概念
最好从广义线性模型的角度分析,逻辑回归是假设y服从Bernoulli分布
3.L1-norm和L2-norm
其实稀疏的根本还是在于L0-norm也就是直接统计参数不为0的个数作为规则项,但实际上却不好执行于是引入了L1-norm;而L1norm本质上是假设参数先验是服从Laplace分布的,而L2-norm是假设参数先验为Gaussian分布,我们在网上看到的通常用图像来解答这个问题的原理就在这。
但是L1-norm的求解比较困难,可以用坐标轴下降法或是最小角回归法求解。
4.LR和SVM对比
首先,LR和SVM最大的区别在于损失函数的选择,LR的损失函数为Log损失(或者说是逻辑损失都可以)、而SVM的损失函数为hinge loss。 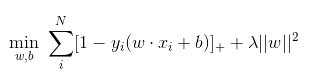
其次,两者都是线性模型。
最后,SVM只考虑支持向量(也就是和分类相关的少数点)
5.LR和随机森林区别
随机森林等树算法都是非线性的,而LR是线性的。LR更侧重全局优化,而树模型主要是局部的优化。
6.常用优化算法
逻辑回归本身是可以用公式求解的,但是因为需要求逆的复杂度太高,所以才引入了梯度下降算法。
一阶方法:梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
二阶方法:牛顿法、拟牛顿法:
这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
拟牛顿法: 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、 L-BFGS(可以减少BFGS所需的存储空间)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号