一：学习总结
1查找结构思维导图
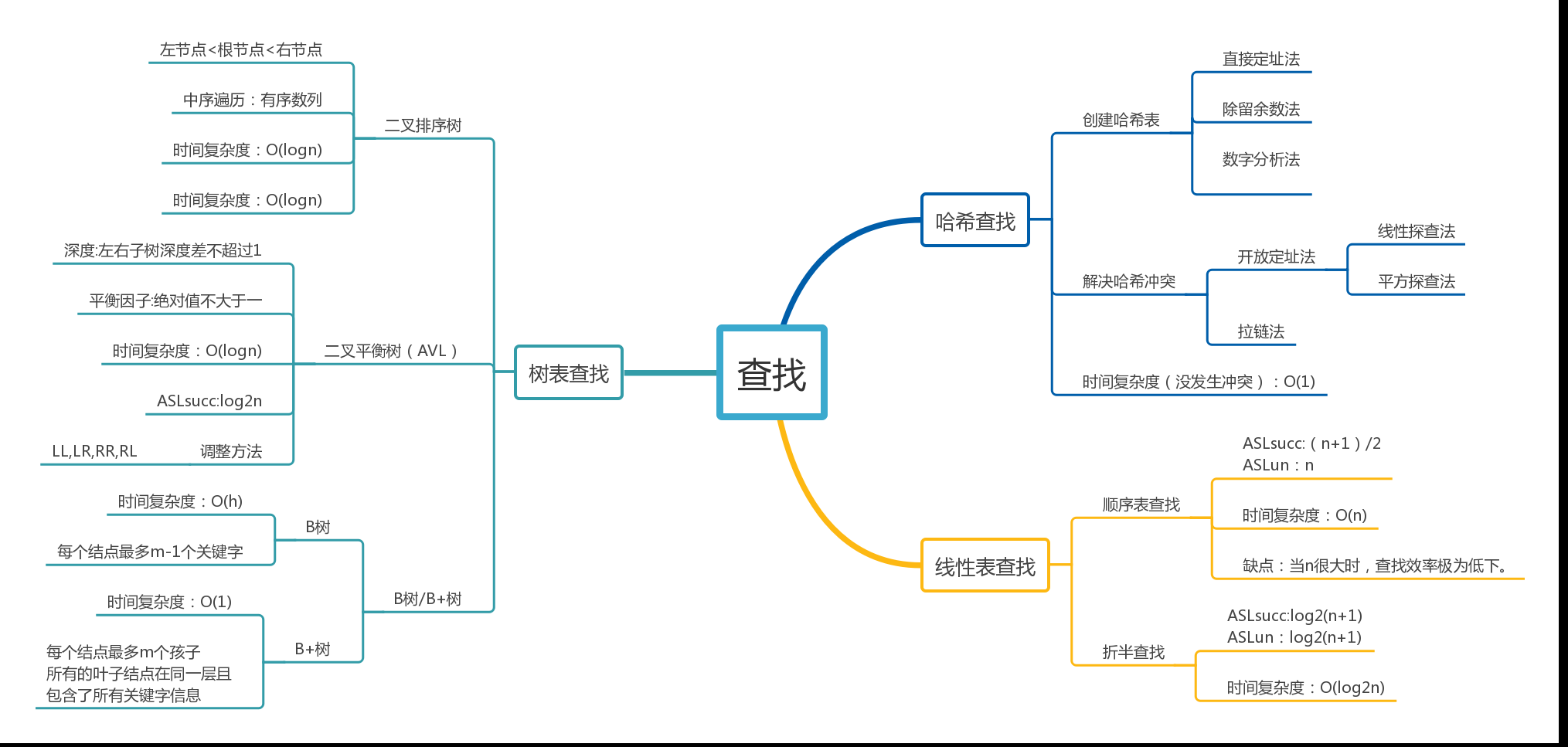
2查找学习体会
查找的内容很多，计算平均查找度的方法也不同，时间复杂度也不同，但是效率真的能提高很多，就是各种概念之间容易混乱，需要花时间认真研究。折半查找过程可用二叉树来描述，二叉排序树的插入与建立，删除又和二叉平衡树的四种调整方式相关，以便获得更高的执行效率，包括哈希表及哈希冲突的各种解决方法等等，如果能掌握好，再加上递归，可以大大减少代码量，比如：判断二叉搜索树和寻找最近公共祖先。
二：PTA实验作业
题目1：是否是二叉搜索树
1设计思路
bool IsBST( BinTree T )
{
若T是空树则是二叉搜索树；
中序遍历该树得到的新节点的值一定要大于前一个值，否则不是；
返回真；
}
2代码截图
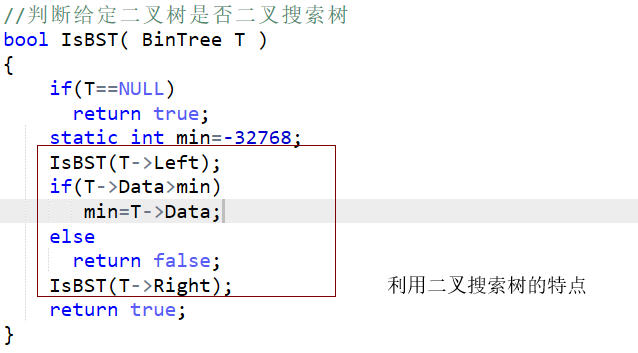
3PTA提交列表说明
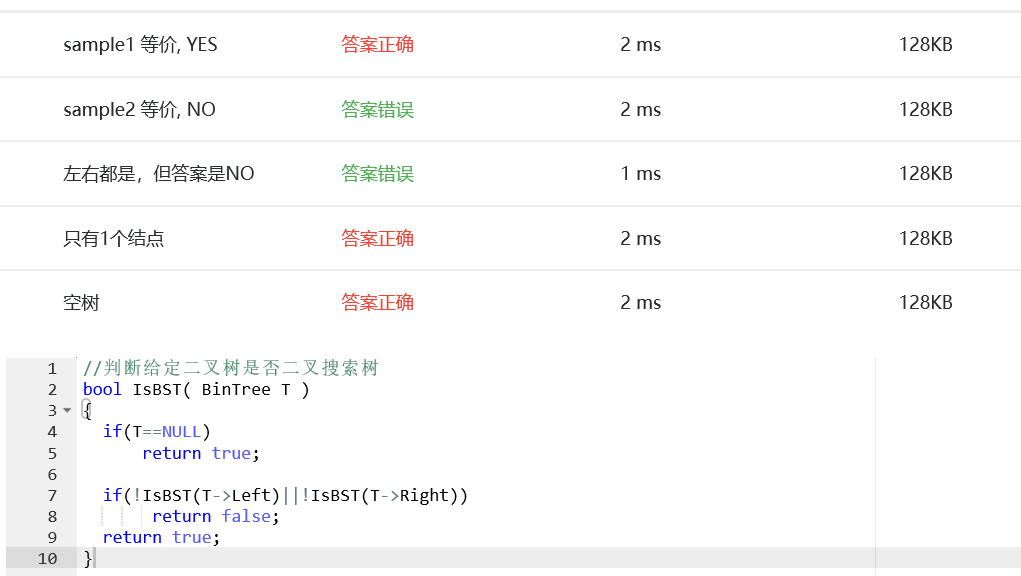
部分正确：最开始只考虑了很简单的情况。
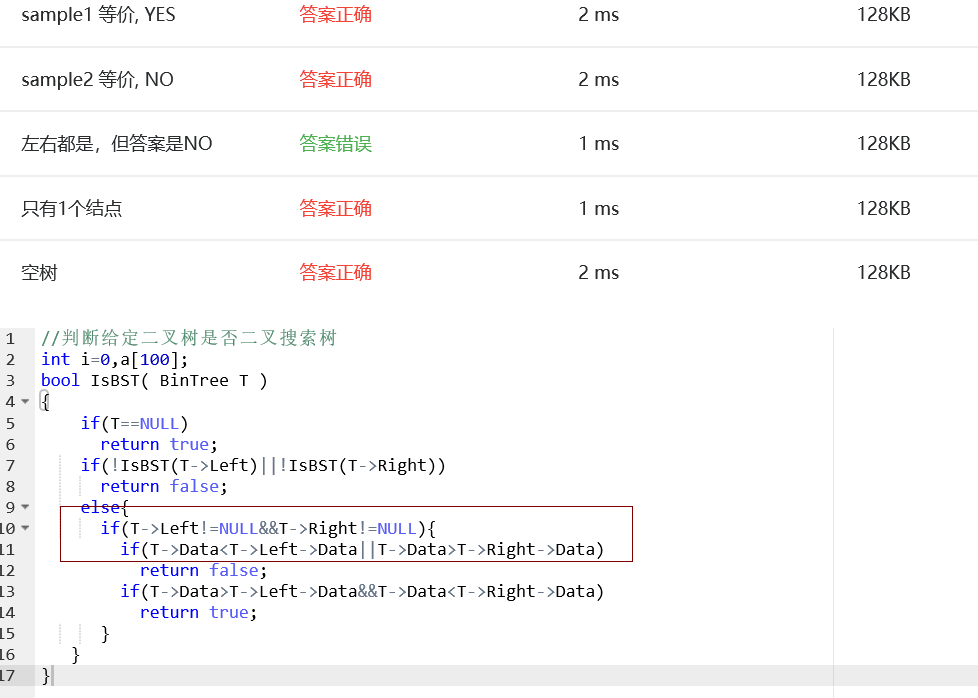
只考虑在根节点出现左、右子树都是二叉搜索树，但是整棵树不是这种情况，但是其实其他地方也会出现，，，用老师提醒的中序遍历思路加上递归重新写了一遍。递归用对了真的非常好用。
题目2：二叉搜索树中的最近公共祖先
1设计思路
int search(Tree T,int u);
int LCA( Tree T, int u, int v )//寻找u,v的共同祖先
{
若树为空或者u或v不在该树中 ERROR;
若u或者v就是根节点的值 return T->Key;
若u或者v在同一棵子树上 return T->Key;
若u大于T->key 最近共同祖先在左子树上;
若u大于T->key 最近共同祖先在右子树上;
}
int search(Tree T,int u)//查看u是否在树中
{
若树为空：则不在；
查找该树：
若找到等值的key，则u在该树中；
否则不在；
}
2代码截图
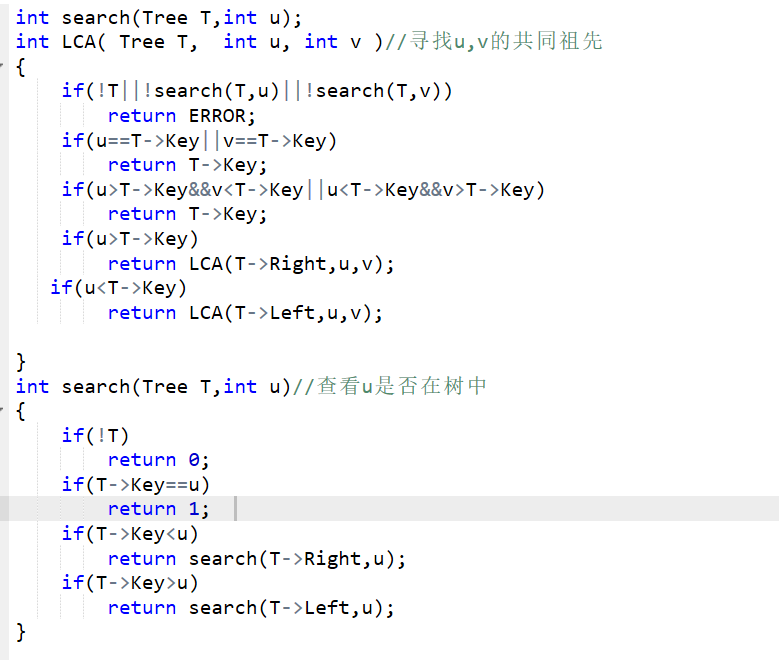
3PTA提交列表说明
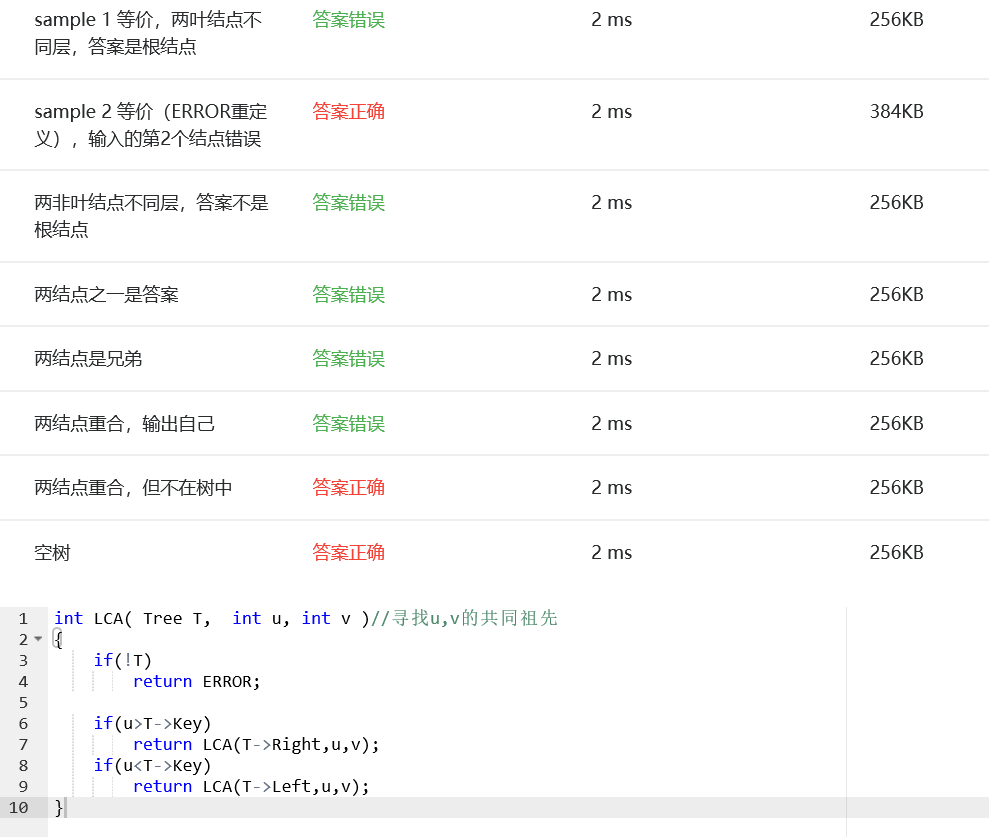
部分正确：有较多种情况没有考虑到，比如当前节点即为公共祖先或者是关键字不在树中。
补充后：
判断关键字是否在树中需要查找该树，所以后来再写了一个查找函数，判断关键字是否在树中，若不在则没有必要继续查找，直接结束。
题目3：QQ帐户的申请与登陆
1设计思路
while(N--){
输入命令符，QQ号码，密码;
判断命令符：
如果是新帐户申请
if(mapQQ.count(Num)) 已经存在该用户;
else 存入新信息;
老用户登录
if(!mapQQ.count(Num)) 不存在该用户;
else
if(mapQQ[Num]==M) 登录成功;
else 密码错误;
}
2代码截图
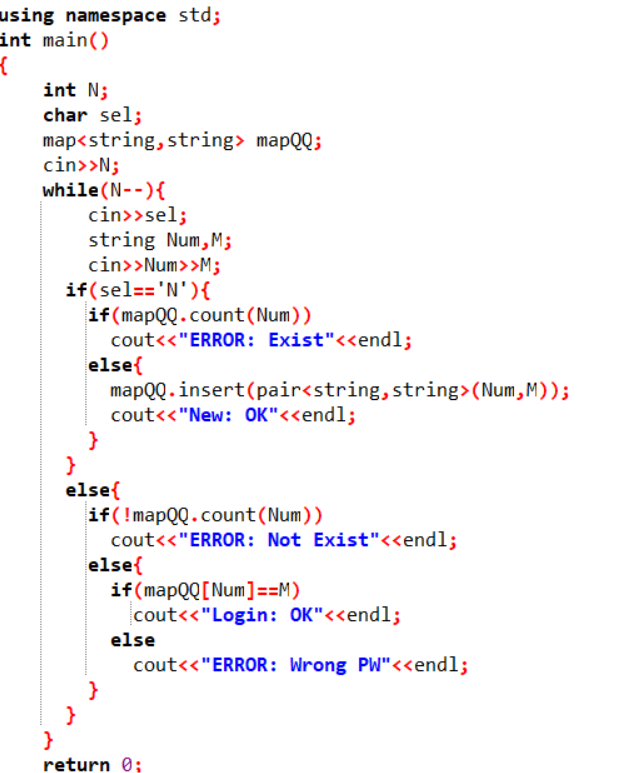
3PTA提交列表说明
刚开始用map还是不怎么会用，老是编译错误，而且有时候晕乎乎的，找不到错误；这道题如果没有用map代码量肯定不会这么少，所以map也是很好用的；
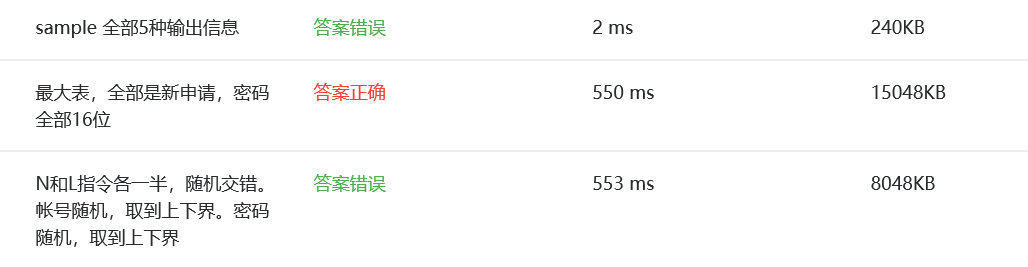
部分正确：感觉是老用户的某个地方出错，仔细检查了一下发现输出的内容在修改的过程中没有对应上，所以出错了，又是不够细致导致的失误！！！
三：截图本周题目集的PTA最后排名
1 PTA排名：
2 我的得分：145
四：阅读代码
旋转数组的最小数字
题目描述：
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3，4，5，1，2}为{1，2，3，4，5}的一个旋转，该数组的最小值为1.
int Min(int *numbers , int length)
{
if(numbers == NULL || length <= 0)
return;
int index1 = 0;
int index2 = length - 1;
int indexMid = index1;
while(numbers[index1] >= numbers[index2])
{
if(index2 - index1 == 1)
{
indexMid = index2;
break;
}
indexMid = (index1 + index2) / 2;
//如果下标为index1、index2和indexMid指向的三个数字相等，则只能顺序查找
if(numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1])
return MinInOrder(numbers , index1 , index2);
if(numbers[indexMid] >= numbers[index1])
index1 = indexMid;
else if(numbers[indexMid] <= numbers[index2])
index2 = indexMid;
}
return numbers[indexMid];
}
//顺序查找
int MinInOrder(int *numbers , int index1 , int index2)
{
int result = numbers[index1];
for(int i = index1 + 1 ; i <= index2 ; ++i)
{
if(result > numbers[i])
result = numbers[i];
}
return result;
}
当两个指针指向的数字及他们中间的数字三者相同的时候，我们无法判断中间的数字是位于前面的字数组还是后面的子数组中，也就无法移动两个指针来缩小查找的范围。此时，我们采用了顺序查找的方法。
五：代码提交
