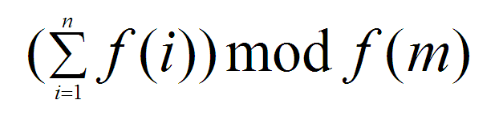蓝桥杯 复习

猴子吃包子

#include <iostream> 
#include<iomanip>
using namespace std;

int main()
{
	double x,y,z;
	double x1,y1,z1;
	int p;
	cin>>x>>y>>z>>x1>>y1>>z1>>p;
	cout<<setiosflags(ios::fixed)<<setprecision(p)<<(x1/x+y1/y+z1/z);
 } 

 景点游览

#include <iostream> 
#include<iomanip>
using namespace std;

int main()
{
	int n;
	cin>>n;
	int s[10000];
	for(int i=0;i<n;i++)
	{
		cin>>s[i];
	} 
	for(int i=0;i<n-1;i++)
		for(int j=0;j<n-1-i;j++)
		{
			if(s[j]<s[j+1])
			{
				int q=0;
				q=s[j];
				s[j]=s[j+1];
				s[j+1]=q;
			}
		}
	for(int i=0;i<n;i++)
	{
		cout<<s[i]<<" ";
	} 
 } 

发糖果

问题描述

　　有n个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果，然后进行下面的游戏：

　　每个小朋友都把自己的糖果分一半给左手边的孩子。

　　一轮分糖后，拥有奇数颗糖的孩子由老师补给1个糖果，从而变成偶数。

　　反复进行这个游戏，直到所有小朋友的糖果数都相同为止。

　　你的任务是预测在已知的初始糖果情形下，老师一共需要补发多少个糖果。

输入格式

　　程序首先读入一个整数N(2<N<100)，表示小朋友的人数。
　　接着是一行用空格分开的N个偶数（每个偶数不大于1000，不小于2）

输出格式

　　要求程序输出一个整数，表示老师需要补发的糖果数。

样例输入

3
2 2 4

样例输出

4

#include <iostream> 
#include <iomanip>
#include <cstdlib>
using namespace std;

int main()
{
	int n;
	int candy[100];
	int candynew[100];
	int flag=0;
	int extra=0;
	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>candy[i];
		/*
		candy[i]=(rand() % (1000-2+1))+ 2; 
		if(candy[i]%2!=0)candy[i]=candy[i]+1;
		*/
		//cout<<candy[i]<<endl;
	}
	int i=0;
	while(flag!=1)
	{
		i++;
		//cout<<i<<"轮"<<endl;
		for(int i=0;i<n;i++)
		{
			if(i==0)candynew[0]=candy[0]/2+candy[n-1]/2;
			else candynew[i]=candy[i]/2+candy[i-1]/2;
			//cout<<candynew[i]<<" "; 
		}
		//cout<<endl;
		for(int i=0;i<n;i++)
		{
			if(candynew[i]%2!=0)
			{
				candynew[i]=candynew[i]+1;
				extra++;
			}
			candy[i]=candynew[i];
			//cout<<candynew[i]<<" ";
		}
		flag=1;
		for(int i=0;i<n-1;i++)
		{
			if(candy[i]!=candy[i+1])flag=0;
		}
		if(flag==1)cout<<extra;
		//if(flag==1)cout<<"游戏结束,补发糖果数："<<extra<<endl; 
		//system("pause");
	}
} 

随机偶数的生成

要取得[a,b]的随机整数，使用(rand() % (b-a+1))+ a; 

斐波那契

问题描述

　　斐波那契数列大家都非常熟悉。它的定义是：

　　f(x) = 1 .... (x=1,2)
　　f(x) = f(x-1) + f(x-2) .... (x>2)

　　对于给定的整数 n 和 m，我们希望求出：
　　f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大，所以我们把它对 f(m) 取模。
　　公式如下


　　但这个数字依然很大，所以需要再对 p 求模。

输入格式

　　输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)

输出格式

　　输出为1个整数，表示答案

样例输入

2 3 5

样例输出

0

样例输入

15 11 29

样例输出

25

#include <iostream> 
using namespace std;

int fib(int x)
{
	if(x<=0) return 0;
    if(x<=2) return 1;
    return fib(x-1)+fib(x-2);
} 

int main()
{
	int n,m,p=0;
	int sum=0;
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++)
	{
		sum=sum+fib(i);
	}
	int res=fib(m);
	cout<<(sum%res)%p;
}

运行超时

分解质因数

#include <iostream>
using namespace std;
//将一个正整数分解质因数  
int main()  
{  
    int i,n;  
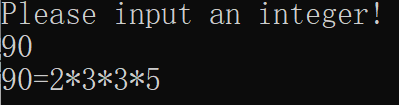
    printf("Please input an integer!\n");  
    scanf("%d",&n);  
    cout<<n<<"="; 
    for(i=2;i<=n;i++)  
    {  
        while(n!=i)     //若i=n，则质因数就是n本身  
        {  
            if(n%i==0)  //若i是质因数，则打印出i的值，并用商给n赋新值  
            {  
                printf("%d",i);  
                n=n/i;  
            }  
            else break;//若不能被i整除，则算下一个i  
            cout<<"*";
        }  
    }  
    printf("%d\n",n);   //这里是打印最后一个质因数，也就是等于i时的那个  
    return 0;  
}  

分核桃

#include <iostream>
using namespace std;

int dis(int n,int s[])  
{  
	/*cout<<n<<"分解为：";*/ 
    int i; 
	int k=1; 
    //printf("Please input an integer!\n");  
    //scanf("%d",&n);  
    //cout<<n<<"="; 
    for(i=2;i<=n;i++)  
    {  
        while(n!=i)     //若i=n，则质因数就是n本身  
        {  
            if(n%i==0)  //若i是质因数，则打印出i的值，并用商给n赋新值  
            {  
            	s[k]=i;k++;
                //printf("%d",i);  
                n=n/i;  
            }  
            else break;//若不能被i整除，则算下一个i  
            //cout<<"*";
        }  
    } 
	s[k]=n; 
	s[0]=k;//数组第0个元素：存放因素个数 
	/*for(i=1;i<=k;i++)
		cout<<s[i]<<" "; 
	cout<<endl;
	cout<<"分解因数个数："<<s[0]<<endl; */
    //printf("%d\n",n);   //这里是打印最后一个质因数，也就是等于i时的那个  
    return 0;  
}  

int check(int a[],int b[])
{
	for(int i=1;i<10;i++)
	{
		for(int j=1;j<10;j++)
		{
			if(a[i]==b[j]&&a[i]!=1&&b[j]!=1)
			{
				b[j]=1; //公有的因数只计算一个 
				break;//比到相同的，消去一个 
			} 
		}
		/*if(a[i]==b[i])
		{
			b[i]=1; //错误写法 
		}*/
		if(a[i]==0)
		{
			a[i]=1;
		}
		if(b[i]==0)
		{
			b[i]=1;
		}
	}
	/*for(int i=0;i<10;i++)
		cout<<a[i]<<" ";
	cout<<endl;
	for(int i=0;i<10;i++)
		cout<<b[i]<<" ";
	cout<<endl;*/
}

int zxgbs(int a[],int b[])
{
	int res=1;
	for(int i=1;i<10;i++)
	{
		res=res*a[i]*b[i];
	}
	return res;
}

int main()
{
		int a,b,c;
		int x[10]={1};
		int y[10]={1};
		int z[10]={1};
		cin>>a>>b>>c;
		dis(a,x);
		dis(b,y);
		dis(c,z);
		check(x,y);
		int temp[10]={1};
		dis(zxgbs(x,y),temp);
		/*for(int i=0;i<10;i++)
			cout<<temp[i]<<" ";
		cout<<endl;*/ 
		check(temp,z);
		cout<<zxgbs(temp,z)<<endl;
}