蓝桥杯 分核桃

问题描述

小张是软件项目经理，他带领3个开发组。工期紧，今天都在加班呢。为鼓舞士气，小张打算给每个组发一袋核桃（据传言能补脑）。他的要求是：

1. 各组的核桃数量必须相同

2. 各组内必须能平分核桃（当然是不能打碎的）

3. 尽量提供满足1,2条件的最小数量（节约闹革命嘛）

输入格式

输入包含三个正整数a, b, c，表示每个组正在加班的人数，用空格分开（a,b,c<30）

输出格式

输出一个正整数，表示每袋核桃的数量。

样例输入1

2 4 5

样例输出1

20

样例输入2

3 1 1

样例输出2

3

OJ版

#include <iostream>
using namespace std;

int dis(int n,int s[])  //将一个数分解质因数，并存放至对应数组中
{  
    int i; 
	int k=1; 
    for(i=2;i<=n;i++)  
    {  
        while(n!=i)     //若i=n，则质因数就是n本身  
        {  
            if(n%i==0)  //若i是质因数，则打印出i的值，并用商给n赋新值  
            {  
            	s[k]=i;k++;
                n=n/i;  
            }  
            else break;//若不能被i整除，则算下一个i  
        }  
    } 
	s[k]=n; 
	s[0]=k;//数组第0个元素：存放因素个数 
    return 0;  
}  

int check(int a[],int b[])//合并共有因数
{
	for(int i=1;i<10;i++)
	{
		for(int j=1;j<10;j++)
		{
			if(a[i]==b[j]&&a[i]!=1&&b[j]!=1)
			{
				b[j]=1; //公有的因数只计算一个 
				break;//比到相同的，消去一个 
			} 
		}
        //为了后续乘法运算，将0全部替换为1
		if(a[i]==0)
		{
			a[i]=1;
		}
		if(b[i]==0)
		{
			b[i]=1;
		}
	}
}

int zxgbs(int a[],int b[])//求最小公倍数，将共有因数与私有因数相乘即可
{
	int res=1;
	for(int i=1;i<10;i++)
	{
		res=res*a[i]*b[i];
	}
	return res;
}

int main()
{
		int a,b,c;
		int x[10]={0};
		int y[10]={0};
		int z[10]={0};
		cin>>a>>b>>c;
		dis(a,x);
		dis(b,y);
		dis(c,z);
		check(x,y);
		int temp[10]={0};
		dis(zxgbs(x,y),temp);
		check(temp,z);
		cout<<zxgbs(temp,z)<<endl;
}

动态解释版

#include <iostream>
using namespace std;

int dis(int n,int s[])  
{  
	cout<<n<<"分解为："; 
    int i; 
	int k=1; 
    //printf("Please input an integer!\n");  
    //scanf("%d",&n);  
    //cout<<n<<"="; 
    for(i=2;i<=n;i++)  
    {  
        while(n!=i)     //若i=n，则质因数就是n本身  
        {  
            if(n%i==0)  //若i是质因数，则打印出i的值，并用商给n赋新值  
            {  
            	s[k]=i;k++;
                //printf("%d",i);  
                n=n/i;  
            }  
            else break;//若不能被i整除，则算下一个i  
            //cout<<"*";
        }  
    } 
	s[k]=n; 
	s[0]=k;//数组第0个元素：存放因素个数 
	for(i=1;i<=k;i++)
		cout<<s[i]<<" "; 
	cout<<endl;
	cout<<"分解因数个数："<<s[0]<<endl; 
    //printf("%d\n",n);   //这里是打印最后一个质因数，也就是等于i时的那个  
    return 0;  
}  

int check(int a[],int b[])
{
	for(int i=1;i<10;i++)
	{
		for(int j=1;j<10;j++)
		{
			if(a[i]==b[j]&&a[i]!=1&&b[j]!=1)
			{
				b[j]=1; //公有的因数只计算一个 
				break;//比到相同的，消去一个 
			} 
		}
		/*if(a[i]==b[i])
		{
			b[i]=1; //错误写法 
		}*/
		if(a[i]==0)
		{
			a[i]=1;
		}
		if(b[i]==0)
		{
			b[i]=1;
		}
	}
	for(int i=0;i<10;i++)
		cout<<a[i]<<" ";
	cout<<endl;
	for(int i=0;i<10;i++)
		cout<<b[i]<<" ";
	cout<<endl;
}

int zxgbs(int a[],int b[])
{
	int res=1;
	for(int i=1;i<10;i++)
	{
		res=res*a[i]*b[i];
	}
	return res;
}

int main()
{
	while(1)
	{
		int a,b,c;
		int x[10]={1};
		int y[10]={1};
		int z[10]={1};
		cin>>a>>b>>c;
		dis(a,x);
		dis(b,y);
		dis(c,z);
		check(x,y);
		int temp[10]={1};
		dis(zxgbs(x,y),temp);
		for(int i=0;i<10;i++)
			cout<<temp[i]<<" ";
		cout<<endl;
		check(temp,z);
		cout<<zxgbs(temp,z)<<endl;
		system("pause"); 
	} 
}

算法：

求小公倍数

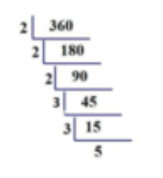
一、分解质因数

二、共有因数与私有因数相乘（共有因数只计算一次）

求三个数的最小公倍数

一、先求两个数的最小公倍数

二、再求前两个数的最小公倍数与第三个数的最小公倍数

分解质因数的方法

对N分解质因数，依次用2~N去除

循环：

【如果可以整除，那么这个数Q是N的因数，用除得结果作为新的N再继续除

如果不能整除，则换下一个除数去除】

除到最后N与除数相等，则这个因数就是N本身，计算完毕

得到的所有的Q就是N的全部因数

总结：

用分解质因数法求最小公倍数，这个算法近似于人的思维，对人来说易于理解，但不好用计算机的语言描述。

穷举法求最小公倍数

居然这么简单？？

#include <iostream>
using namespace std;

int zxgbs(int a,int b)
{
	int i;
	for (i=a;;i++)
        if ( i % a == 0 && i % b ==0 )
		  	break;
    return i;
} 

int main()
{
	int a,b,c;
	cin>>a>>b>>c;
	int res=zxgbs(zxgbs(a,b),c);
	cout<<res;
}

血亏..