| 项目 | 内容 |
|---|---|
| 班级博客链接 | 班级博客 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | （1）掌握软件项目个人开发流程 （2）掌握Github发布软件项目的操作方法 （3）掌握动态规划的应用 |
| 这个作业在哪些方面帮助我实现学习目标 | （1）对动态规划和回溯算法的学习，巩固书写代码的能力 （2)培养同学间的互助能力 |
-
任务3
-
需求分析
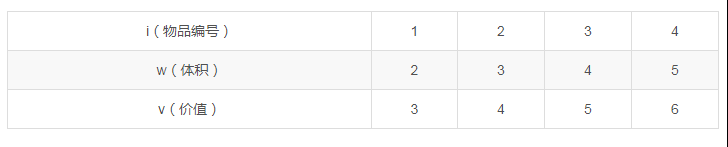
问题：有n个物品，它们有各自的体积和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？
例如：number＝4，capacity＝8
-
功能设计
-
基本功能
1）可正确读入实验数据文件的有效D{0-1}KP数据；2）能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图；
3） 能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序；
-
用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间（以秒为单位）；
-
任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
-
-
-
设计实现
动态规划：动态规划与分治法类似，都是把大问题拆分成小问题，通过寻找大问题与小问题的递推关系，解决一个个小问题，最终达到解决原问题的效果。但不同的是，分治法在子问题等上被重复 计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，
所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。问题分析:令V(i，j)表示在前i(1<=i<=n)个物品中能够装入容量为就j(1<=j<=C)的背包中的物品的最大价值，则可以得到如下的动态规划函数: (1)v(i,0)=V(O,j)=0 (2)V(i，j)=V(i-1,j) j<wi V(i,j)=max{V(i-1,j) ,v(i-1,j-wi)+Vi)}j>wi (1)式表明:如果第i个物品的重量大于背包的容量，则装人前i个物品得到的最大价值和装入前i-1个物品得到的最大价是相同的，即物品i不能装入背包;第(2)个式子表明:如果第i个物品的重 量小于背包的容量，则会有一下两种情况:(a)如果把第i个物品装入背包，则背包物品的价值等于第i-1个物品装入容量位j-wi的背包中的价值加上第i个物品的价值vi;(b)如果第i个物品没 有装入背包，则背包中物品价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。显然，取二者中价值最大的作为把前i个物品装入容量为j的背包中的最优解。回溯法：为了避免生成那些不可能产生最佳解的问题状态，要不断地利用限界函数来处死那些实际上不可能产生所需解的活结点，以减少问题的计算量。
对于有n种可选物品的0/1背包问题，其解空间由长度为n的0-1向量组成,可用子集数表示。在搜索解空间树时，只要其左儿子结点是一个可行结点，搜索就进入左子树。当右子树中有可能包含最优解时就进入右子树搜索。
-
测试运行
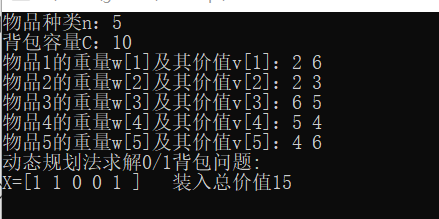
动态规划：
回溯：
-
代码展示
if(cw + goods[i].wight <= C){//进入左子树 cw += goods[i].wight; cv += goods[i].value; cx[i] = 1;//装入背包 BackTrack(i+1); cw -= goods[i].wight; cv -= goods[i].value;//回溯，进入右子树 } -
PSP展示
-
| PSP各个阶段 | 各阶段用时（min） |
|---|---|
| 计划 | 40 |
| 明确需求和其他因素，估计各个阶段所用时 | 40 |
| 开发 | 419 |
| 需求分析 | 30 |
| 生成设计文档 | 20 |
| 设计审核 | 20 |
| 代码规范 | 15 |
| 具体设计 | 25 |
| 具体编码 | 290 |
| 代码复审 | 40 |
| 测试 | 15 |
| 报告 | 130 |
| 测试报告 | 70 |
| 计算工作量 | 35 |
| 事后总结，并总结过程改进计划 | 25 |
