线性复杂度优化小技巧
六个小技巧
1.前缀和
2.差分
3.双指针
4.离散化
5.单调队列
6.单调栈
前缀和
前缀和顾名思义,前面的和,具体来说就是前n项的和
sum为前缀和数组
一维前缀和
第n项的前缀和等于第n-1项前缀和+第i项数之和
\(\sum_{1}^{n}a[i]=\sum_{1}^{n-1}a[i]+a[i]\)
sum[i]=sum[i-1]+a[i];
应用
求静态区间和
例如求 a[i]区间[l,r]的和
\(\sum_{i=l}^{r}a[i]=\sum_{i=1}^{r}a[i]-\sum_{i=1}^{l-1}a[i]\)
二维前缀和
\(\sum_{i=1}^{n}\sum_{j=1}^{n}a[i][j]=\sum_{i=1}^{n-1}\sum_{j=1}^{n}a[i][j]+\sum_{i=1}^{n}\sum_{j=1}^{n-1}a[i][j]+a[n][n]-\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}a[i][j]\)
(至于怎么推出来的,建议自行画个图表示一下)
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]
应用与一维类似
差分
差分 为 相差的数
一维差分
定义cf[n]为差分序列
\(cf[i]=a[i]-a[i-1]\)
应用
区间求加数后的第i个数
例如一个区间[l,r]都加上一个数x,求第i个数
求第n个数,设第i个数为y
\(y=\sum_{i=1}^{n}cf[i]\)
- 证明
(设a[0]=0,不影响结果
\(cf[n]=a[n]-a[n-1]\)
\(cf[n-1]=a[n-1]-a[n-2]\)
\(..........\)
\(cf[2]=a[2]-a[1]\)
\(cf[1]=a[1]-a[0]\)
各式相加
\(\sum_{i=1}^{n}cf[i]=a[n]\)
证毕
当[l,r]加上一个数x,cf[l+1,r]都不会发生改变
只有\(cf[l]=a[l]+x-a[l-1]=cf[l]+x,cf[r+1]=a[r+1]-(a[r]+x)=cf[r+1]-x\)
二维差分
\(a[i]=sum[i]-sum[i-1]\)
\(cf[i]=a[i]-a[i-1]\)
这里借鉴一维的变化
推出二维的差分
(为什么能推出来,因为前缀和的差分就是原数列,又因为差分的前缀和是原数列,所以由前缀和差分得到的原序列同样适用于由原序列差分得到差分序列)
\(a[i][j]=sum[i][j]-sum[i-1][j]-sum[i][j-1]+sum[i-1][j-1]\)
\(cf[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]\)
应用与一维类似
至于与一位的差异
比如给以\(x_1,y_1\)为左上角,\(x_2,y_2\)为右下角的矩阵都加上x
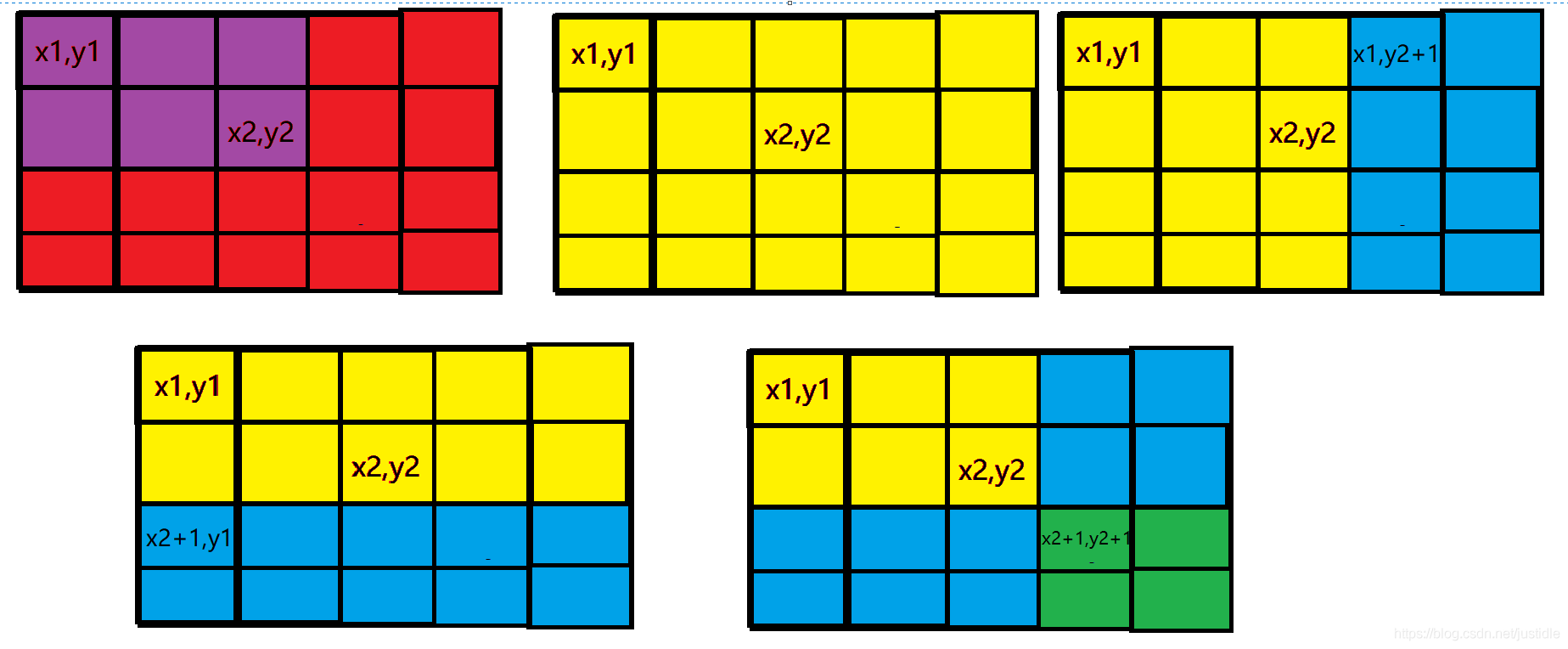
此时cf数组就要进行如下操作
cf[x1][y1]+=x;
cf[x1][y2+1]-=x;
cf[x2+1][y1]-=x;
cf[x2+1][y2+1]+=x;
依次来看
根据前缀和性质
\(cf[x1][y1]+=x\) 整个黄色部分在求其a[i][j]\(i>x_1 和j>y_1\)时都会因其影响
\(cf[x1][y2+1]-=x\) 同理蓝色部分会消除影响
\(cf[x2+1][y1]-=x\) 同理蓝色部分会消除影响
\(cf[x2+1][y2+1]+=x\) 消除两个蓝色过度消除的影响
总结下前缀和和差分,两个为互逆的运算
离散化(李三花
离散化是在考虑数与数之间的大小关系而不考虑具体数值的情况下使用
比如序列 \(1,100000,2999\)
有两种离散化方式
这里介绍一种
以值为排序,用下标代替原来的值
容易知道 \(1,2999,100000\)
下标代替原来的值为\(1,2,3\)
struct node{
int val,p;
}s[maxn];
bool cmp(node a,node b){
return a.val<b.val;
}
sort(s+1,s+1+n,cmp);
双指针
双指针不是c语言中的指针
而是用两个变量遍历
举例就懂了,比如二分查找时的l,r 还有就是现在手写快速排序时,左右指针找大于小于中间数的值
单调队列
思路就是两遍跑单调队列
一遍维护单调递增序列,一遍维护单调递减序列
重点介绍怎么维护单调队列
单调队列,是在队列的基础上,使队列同样具有单调性(注意区分单调队列和优先队列)这个单调性可根据自己定义来(最小值啊,最大值啊,其他...
-
模拟一遍就懂了
窗口长度为3
1 3 -1 -3 5 3 6 7这遍取最小值(相当于维护单调递增队列)
q为维护的单调队列,p为相对应数的下标1入队
\(q=[1],p=[1]\)
3入队
$ q=[1,3],p=[1,2]$
因为3比1大且下标更大,所以有可能在滑动窗口后能为最小值
-1入队
$ q=[-1],p=[3]$
因为-1比1,3都小,可以挤掉前面的数,而且下标更大,更有可能满足答案的条件
此时区间长度已为3,下一次就会滑动窗口,所以现在输出队中最小值,即为-1
接下来每次都会滑动窗口使一个新数入列
-3入队,同上挤掉-1
\(q=[-3],p=[4]\)
按照上述描述
依次队列的变化
\(q=[-3,5],p=[4,5]\)
\(q=[-3,3],p=[4,6]\)
最小值仍然为-3,但下一窗口滑动就不能取-3,此时下标不在窗口内,需要弹出-3
所以下次队列
\(q=[3,6],p=[6,7]\)
依次
\(q=[3,6,7],p=[6,7,8]\)
\(q=[6,7],p=[7,8]\)
\(q=[7],p=[8]\)
over
CODE
#include<cstdio>
using namespace std;
int n,k;
int a[1000000+10];
int q[1000000+10],p[1000000+10];
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int head=1,tail=0;
for(int i=1;i<=n;i++)
{
while(head<=tail && q[tail]>=a[i]) --tail;//找到比他小的数为止
q[++tail]=a[i];//否则入队列
p[tail]=i;
while(p[head]<=i-k) head++;//窗口后移一次,第一个元素过时 下标比较
if(i>=k) printf("%d ",q[head]); //i大于窗口长度时循环一次输出一次 输出队列最小值
}
printf("\n");
head=1,tail=0;//重置队列,再次重新从头找最大值
for(int i=1;i<=n;i++)
{
while(head<=tail && q[tail]<=a[i]) tail--;//找到比他大的数为止
q[++tail]=a[i];//否则入队列
p[tail]=i;
while(p[head]<=i-k) head++;//窗口后移一次,第一个元素过时 下标比较
if(i>=k) printf("%d ",q[head]); //i大于窗口长度时循环一次输出一次 输出队列最大值
}
}
单调栈
题意简化,找位置i后最大数
单调栈和单调队列类似
1.单调递增栈
2.单调递减栈
这里找一个最大数,可以考虑使用单调递增栈,从后往前扫
保持栈底为最大值,如果有个数比栈顶大或想到,则可以挤掉栈顶的数(悟一下why)
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int n;const int maxn=3e6+10;
int a[maxn],f[maxn];
int st[maxn],top=0;
int main(){
cin>>n;
for(int i=1;i<=n;++i) cin>>a[i];
for(int i=n;i>=1;--i){
while(top && a[st[top]]<=a[i]) --top;
f[i]=!top?0:st[top];
st[++top]=i;
}
for(int i=1;i<=n;++i) cout<<f[i]<<" ";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号