初次接触到ACM,发现有很多的问题都不会
认识到了难度,自己还是蒟蒻(巨弱)啊
这次学到的是一道区域型的动态规划问题吧,虽然对很多人来说很简单
一开都没啥思路就会画个图
后面看了题解才知道要用到动态规划,可是还是不会啊
然后去了解了下,啥叫动态规划问题
动态规划程序设计是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。不像搜索或数值计算那样,具有一个标准的数学表达式和明确清晰的解题方法。
动态规划程序设计往往是针对一种最优化问题,由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,
有各具特色的解题方法,而不存在一种万能的动态规划算法,可以解决各类最优化问题。因此读者在学习时,除了要对基本概念和方法正确理解外,
必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论,
逐渐学会并掌握这一设计方法。
当然上面是百度的。。。
在自己的理解上的话:那此题来说,关键要懂建造一个状态转移方程,啥叫状态转移方程呢?
状态转移方程,是动态规划中本阶段的状态往往是上一阶段状态和上一阶段决策的结果。如果给定了第K阶段的状态Sk以及决策uk(Sk),
则第K+1阶段的状态Sk+1也就完全确定。
也就是说下一步的解取决于上一步(好像有点像递推了)的解,一步一步推到最后一个结果
难点是要如何书写状态转移方程,以及状态转移方程的初始状态是啥(我把他叫做式子的入口)
再利用此方程表达的关系,推出最后的结果
解题的第一步当然是分析题目啦
圆圈为马踏之地,方块为起始位置(不要在意好看不好看啦)
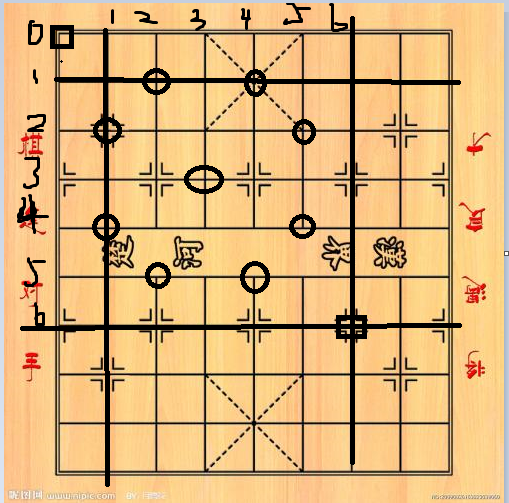
此题建立两个二维数组,第一个horse标记马踏之地(自己所在地别忘咯)
第二个map来解决每一步的解问题
到达一个位置的路径数量来源可到左边与上边那两个位置的数量相加,map[i][j]=map[i-1][j]+map[i][j-1];
当然马拦住的地方的数肯定为0啦
接下来:翠花!上酸菜!

#include<iostream> using namespace std; long long horse[25][25],map[25][25]; void Mark(long long x,long long y) //马能跳的地方 {//因为数组开的足够大所以,不用判断会不会向下和右越界 horse[x][y]=1; if(x-2>=0||y>=1) horse[x-2][y-1]=1; if(y-2>=0&&x>=1) horse[x-1][y-2]=1; if(y-2>=0) horse[x+1][y-2]=1; if(y-1>=0) horse[x+2][y-1]=1; if(x-2>=0) horse[x-2][y+1]=1; if(x-1>=0) horse[x-1][y+2]=1; horse[x+2][y+1]=1; horse[x+1][y+2]=1; } int main() { long long x,y,n,m; cin>>n>>m>>x>>y; Mark(x,y); map[1][0]=1;//我把它叫做:状态转移方程的入口 for(int i=1;i<=n+1;i++)//怕负数,把数组全往右下移动1个单位 { for(int j=1;j<=m+1;j++) { map[i][j]=map[i-1][j]+map[i][j-1];//状态转移方程 if(horse[i-1][j-1])map[i][j]=0; } } cout<<map[n+1][m+1];//往右下移动一个位置咯 return 0; }
最后一步的map情况:
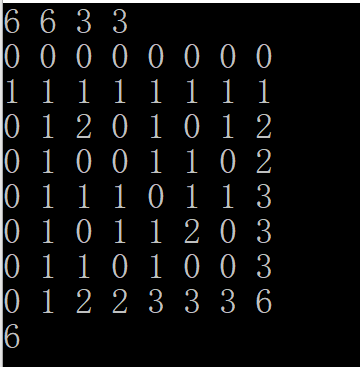
代码的注释也注释了,
不过这只是很简单的一道题,后面还有很多题都不会,好好学吧



