NOIp 数据结构专题总结 (1):STL、堆、并查集、ST表、Hash表
系列索引:
STL structure
STL 在 OI 中的运用:https://oi.men.ci/stl-in-oi/
std::vector
#include <vector>
std::vector<type> v;
v.push_back(x);
v.pop_back();
int *a = new int[N];
std::bitset
#include <bitset>
std::bitset<size> bs;
神似 bool 数组。
SAO操作:
std::bitset<N> g[N]; // store a graph, O(n^2/32)
std::map
#include <map>
std::map<typeA, typeB> mp;
mp[x] = y;
map<int,bool> g[n];
g[x][y] = true;
map<int,bool>::iterator it;
for (it=g[x].begin(); it!=g[x].end(); ++it)
it->first, it->second
std::queue
#include <queue>
std::queue<type> q;
q.push(x);
q.pop();
x = q.front();
std::stack
#include <stack>
std::stack<type> s;
s.push(x);
s.pop();
x = s.top();
std::deque
#include <queue> / #include <deque>
std::deque<type> dq;
std::priority_queue
#include <queue>
std::priority_queue<type> pq; // default: greater first
std::priority_queue<int, std::vector<int>, std::greater<int> > pq; // lower first
struct type { friend bool operator < (type a, type b) {return ...;} };
struct cmp { bool operator() (type a, type b) {return ...;} };
std::priority_queue<type, std::vector<type>, cmp> pq;
std::set
#include <set>
std::set<type> st; // 会自动去重
std::multiset<type> st2; // 不去重
时间复杂度每次操作 \(O(\log{n})\)。
堆 Heap
Pure
复杂度均摊 \(O(\log{n})\).
void put(int x) {
int now = ++heap_size, next;
heap[heap_size] = x;
while (now > 1) {
next = now >> 1;
if (heap[now] >= heap[next]) break; // lower root
swap(heap[now], heap[next]);
now = next;
}
}
int get(int x) {
int now = 1, next, res = heap[1];
heap[1] = heap[heap_size--];
while ((now << 1) <= heap_size) {
next = now << 1;
if (next < heap_size && heap[next+1] < heap[next]) next++;
swap(heap[now], heap[next]);
}
return res;
}
堆的初始化:新建一个空堆,把这些元素依次加进堆,时间 \(O(n\log{n})\)。如果把这些元素 random_shuffle 一下再加进来,期望时间 \(O(n)\)。可以先随意把这些元素放进完全二叉树,再考虑从底向上令每个子树满足堆性质。
堆的删除:因为我们只关心堆顶的元素,我们可以把被删掉的元素暂时留在堆中,并保证当前堆顶的元素未被删除即可。一种实现方法是再开一个堆存储被删除但留在原堆中的元素,一旦两个堆堆顶相等,就一起弹出堆顶。总时间复杂度 \(𝑂(𝑛\log{𝑛})\),这个方法也适用于 std::priority_queue。
STL <algorithm>
void put(int x) {
heap[++heap_size] = x;
// greater heap
push_heap(heap + 1, heap + heap_size + 1);
// lower heap
push_heap(heap + 1, heap + heap_size + 1, greater<int>());
}
int get() {
// greater heap
pop_heap(heap + 1, heap + heap_size + 1);
// lower heap
pop_heap(heap + 1, heap + heap_size + 1, greater<int>());
return heap[heap_size--];
}
STL std::priority_queue
(refer to above)
并查集 Disjoint Set
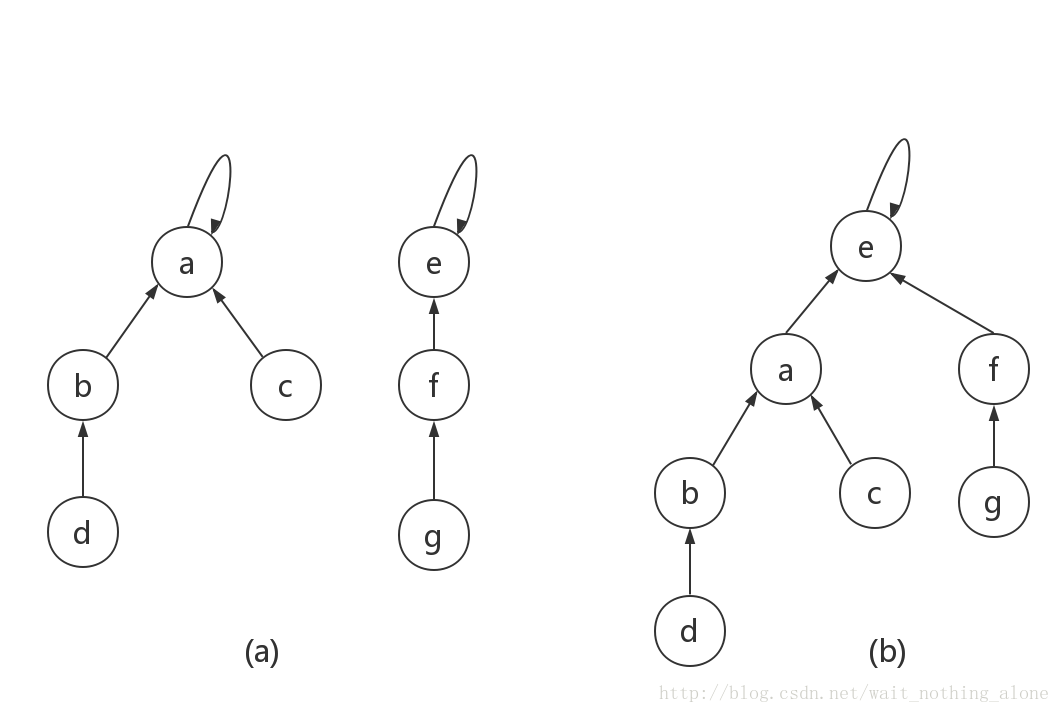
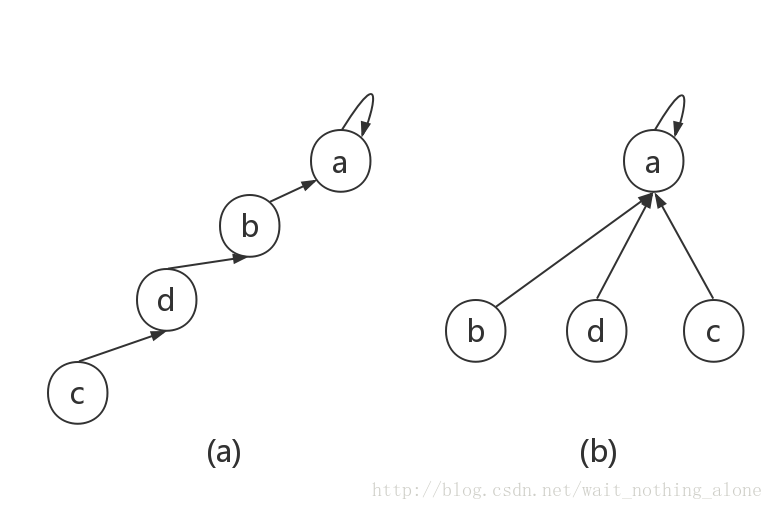
路径压缩优化:查询一个元素时,将其到根路径上所有元素的父亲更新为当前的根。时间复杂度 \(\approx O(n)\)(均摊每次 \(O(1)\))。只用路径压缩优化的并查集实际上能被构造数据卡到 \(O(n\log{n})\)。
for (int i=1; i<=n; i++) fa[i]=i;
int find(int x) {return fa[x]==x ? x : fa[x]=find(fa[x]); }
void join(int x, int y) {x=find(x),y=find(y); fa[x]=y; }
带权并查集:在集合的根上加一个值为 \(x\) 的标记。对于一般的带权并查集,一个元素到根路径上的标记之和就是这个元素的实际权值。路径压缩时需要注意路径压缩对标记效果的影响。
int f[], sum[];
int fa(int x) {
if (f[x]==x) return x;
else {
int r=fa(f[x]);
sum[x]+=sum[f[x]];
return f[x]=r;
}
}
int main() {
int n, m;
while (~scanf("%d%d", &n, &m)) {
for (int i=0; i<=n; ++i) fa[i]=i;
for (int i=1, x, y, z; i<=m; ++i) {
scanf("%d%d%d", &x, &y, &z);
int fx=fa(x), fy=fa(y);
if (fx!=fy) f[fy]=fx, sum[fy]=sum[x]-sum[y]+z; // 类似向量运算
else if (sum[y]-sum[x]!=z) ++ans; // 发现矛盾
}
printf("%d\n", ans);
}
return 0;
}
带权并查集可参考 Link
。
按秩合并优化:“秩”即并查集维护的有根树的深度。合并两个集合时,可以选择深度较小的有根树连接到另一棵上,深度较大的有根树深度会发生改变仅当两树深度相等。如果我们定义一个点的树深度为 \(0\),在这种合并策略下,深度为 \(i\) 的有根树至少有 \(2^i\) 个元素,那么每次操作的时间复杂度显然不超过 \(O(\log{n})\),总时间复杂度 \(O(n\log{n})\)。显然可以在按秩合并的同时采用路径压缩进一步优化,时间复杂度 \(O(n\cdot\alpha(n))\)。
for (int i=1; i<=n; i++) fa[i]=i;
int find(int x) {return fa[x]==x ? x : fa[x]=find(fa[x]); } //有路径压缩
void join(int x, int y) {
x=find(x),y=find(y);
if (rank[x] < rank[y]) fa[x]=y;
else {fa[y]=x; if(rank[x]==rank[y]) ++rank[x]; }
}
操作撤消:未使用任何优化时,直接将合并操作时连接的边删去即可。使用路径压缩优化后,一次合并操作连接的边可能被压缩掉,难以撤销;如果只使用按秩合并优化,显然不会影响撤销操作。支持撤销操作的并查集可以做到 \(O(n\log{n})\) 的总时间复杂度。
按大小合并优化:每次将较小的集合的根连接到较大的上。考虑一个元素到根的路径上,每经过一条边,说明其所在集合的大小至少扩大一倍,显然不超过 \(O(\log{n})\) 条。时间复杂度 \(O(n\log{n})\)。
ST 表 Sparse Table
Range Maximum/Minimum Query:用 \(f(k,i)\) 表示 \([i,i+2^k-1]\) 的最大值,则有 \(f(k+1,i)=\max\{f(k,i),f(k,i+2^k)\}\)(最小值同理)。查询 \([l,r]\) 时,我们找到最小的 \(k\) 满足 \(2^{k+1}\ge r-l+1\),由于重复统计不影响最值,\(\max[l,r]=\max\{f(k,l),f(k,r-2^k+1)\}\)。预处理 \(O(n\log{n})\),每次查询 \(O(1)\)。
inline void ST() {
for (int i=1; i<=n; i++) f[i][0]=data[i];
for (int j=1; (1<<j)<=n; ++j)
for (int i=1; i+(1<<j)-1<=n; ++i)
f[i][j] = max(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
inline int query(int l, int r) {
int k=0;
for (; (1<<k)<=(r-l+1); ++k); --k;
return max(f[l][k], f[r-(1<<k)+1][k]);
}
求 LCA:ST 表 + DFS 序。 (refer to Graph Theory)
Hash 表
将复杂信息按其 Hash 值存储到对应位置上。数组 + 链表。每次期望时间 \(O(1)\)。
自然溢出:高效,省去取模。
保证正确性:
- 模数尽量采用质数,避免被数论相关性质影响。
- 双 Hash:用两种不同的方式求出 Hash 值分别对比。
- 混合 Hash:乘法、加法、异或、取模。
- 随机 Hash 中用到的常数,例如模数、乘数等,避免针对。
杂项
Huffman 树和 Huffman 编码:参考 Link ![]() 。
。
Post author 作者: Grey
Copyright Notice 版权说明: Except where otherwise noted, all content of this blog is licensed under a CC BY-NC-SA 4.0 International license. 除非另有说明,本博客上的所有文章均受 知识共享署名 - 非商业性使用 - 相同方式共享 4.0 国际许可协议 保护。
