前言
符号定义
- \(\breve{x}\) 先验估计
- \(\hat{x}\) 后验估计
- x 真实值
关于KF
卡尔曼滤波是卡尔曼在1960年提出的最优线性的状态估计方法
- 线性:被估计量(即状态量\(x_t\))之间具有线性关系
- 最优:估计误差\((x_t-\hat{x_t})\)具有最小方差
- 无偏:估计误差\((x_t-\hat{x_t})\)的均值为0
综上,KF应该关注的核心概念:估计误差
KF的理想状态:估计值\(\hat{x}\)与真实值\(x\)完全重合。
但是这种理想状态在现实中是不可能实现的,但是我们期望两者尽可能重合,于是提出两项指标来表示重合程度
- 误差均值:\(E[e]\)
- 误差协方差:\(COV[e]\)
我们期望估计值\(x_{t}\)围绕\(x-E[e]\)的上下波动尽可能小,即具有最小方差\(min(COV[e])\),如果可能,\(E[e]\)最好为0
所以KF的核心问题:如何使估计误差\(e_t\)具有最小方差?
KF在控制系统中的作用
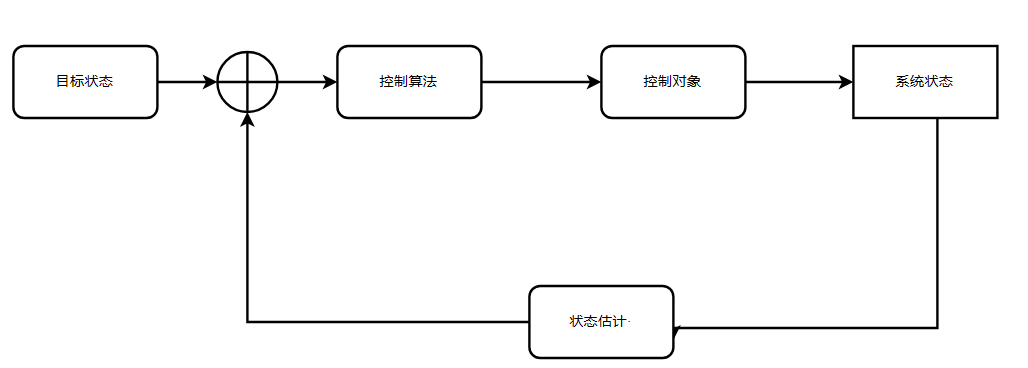
状态估计问题:如何以最好的方式里利用已有传感器
卡尔曼滤波公式(KF)
基本动态系统模型

\[x_t=F_t x_{t-1}+B_tu_t+w_t\\
z_t=H_tx_t+v_t
\]
- \(u_t\)是控制量,\(B_t\)是控制模型
- F是状态转移模型,H是观测模型
- \(w_k\)是过程噪声,\(z_{k}\)是观测噪声,且\(w_k \sim (0,Q_k),z_k \sim (0,R_k)\)
NOTE: 上面两式都有噪声参与,因此\(x_t\)为真实值
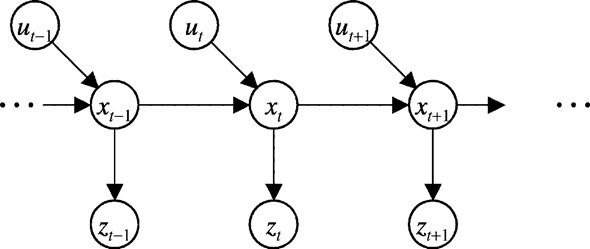
但实际情况,我们难以知道噪声值,因此系统模型变为
\[\breve{x_t}=F_t \hat{x_{t-1}}+B_tu_t\\
z_t=H_tx_t
\]
KF 公式
预测
\[\breve{x_t}=F_t \hat{x_{t-1}}+B_tu_t \cdots预测状态\\
\breve{\Sigma}_t=F_t\hat{\Sigma}_{t-1}F^T_t+Q_t \cdots 预测估计协方差矩阵\\
\]
修正
\[K_t=\breve{\Sigma}_tH^T_t(H_t\breve{\Sigma}_tH^T_t+R_t)^{-1} \cdots 卡尔曼增益\\
\hat{x_t}=\breve{x_t}+K_t(z_t-C_t\breve{x}_t) \cdots 更新状态估计\\
\hat{\Sigma_t}=(I-K_tH_t)\breve{\Sigma}_t \cdots 更新协方差估计
\]
KF的公式推导
了解数据融合的思想
假设有两种方式测量的数据\(a^1,a^2\),它们服从正太分布-\(a^1 \sim (0,\sigma_1^2)\) \(a^2 \sim (0,\sigma_2^2)\),如何将两个数据进行融合?
不妨设\(a_t=a^1_t+K_t(a^2_t-a^1_t)\)为其融合公式,\(K_t\in[0,1]\)代表的是融合的比例.
- \(K_t=0\),\(a_t=a^1_t\)
- \(K_t\)=1,\(a_t=a^2_t\)
设\(a_t\)的方差为\(COV({a_t})\)
\[COV({a_t})=COV((1-K_t)a^1_t+K_ta^2_t)=(1-K_t)^2COV({a^1_t})+(K_t)^2COV({a^2_t})
\]
由题知\(COV(a^1_t)=\sigma^2_1\),\(COV(a^2_t)=\sigma^2_2\)
\[COV(a_t)=(1-K_t)^2 \sigma^2_1+(K_t)^2 \sigma_2^2
\]
\(\therefore\)
\[K_t=\mathop{argmin}_{k_t}(1-K_t)^2 \sigma^2_1+(K_t)^2 \sigma_2^2
\]
对上式进行求导,使得\(\frac{\mathrm{d}(COV(a_t))}{\mathrm{d}K_t}=0\)
\[\frac{\mathrm{d}(COV(a_t))}{\mathrm{d}K_t}=-2(1-K_t) \sigma^2_1+2(K_t) \sigma_2^2=0
\]
\(\therefore\)
融合比例\(K_t\)为
\[K_t=\frac{\sigma^2_1}{\sigma^2_1+\sigma^2_2}
\]
融合后的方差\(COV(a_t)\)为
\[COV(a_t)=\frac{\sigma^2_1\sigma^2_2}{\sigma^2_1+\sigma^2_2}
\]
卡尔曼增益\(K_t\)的推导
已知:
-
\(Q_t=E[w_tw_t^T]\)
-
\(R_t =E[v_tv_t^T]\)
借助数据融合的思想,我们不妨假设一个融合比例\(K_t\),它对于数据融合的公式如下:
\[\hat{x_t}=\breve{x_t}+K_t(z_t-H\breve{x_t})\\
或\\
\hat{x_t}=\breve{x_t}+G_t(H^{-1}z_t-\breve{x_t})
\]
后验状态误差估计为\(\hat{e_t}=x_t-\hat{x_t}=x_t-(\breve{x_t}+K_t(z_t-H\breve{x_t}))\)
我们期望\(\hat{e_t}\) 的均方误差\(E[|x-\hat{x}|^2]\)最小,
上式可归纳为
\[K_t=\mathop{argmin}_{K_t}|\hat{e_t}|^2=\mathop{argmin}_{K_t}|x_t-(\breve{x_t}+K_t(z_t-H\breve{x_t}))|^2
\]
且
\[\hat{e} \sim (0,\hat{\Sigma})
\]
我们希望\(\hat{e_t}\) 的均方误差\(E[|x-\hat{x}|^2]\)最小,也就是说\(\hat{e}\)的分布,尽量靠近其均值0,也就是说其协方差\(\hat{\Sigma}\)要尽可能的小。
但是协方差\(\Sigma\)是一个矩阵,如何评价其大小?
答案是迹,使用\(trace(\hat{\Sigma})\),我们期望通过\(trace(\hat{\Sigma})\),来得到\(K_t\)
\[K_t=\mathop{argmin}_{K_t}{(trace(\hat{\Sigma}))}
\]
又因为
\[\hat{\Sigma}=E[\hat{e}\hat{e}^T]=E[(x_t-\hat{x_t})(x_t-\hat{x_t})^T]
\]
化简\(e_t\)
\[\begin{align}
\hat{e_t} &=x_t-\hat{x_t}\\
&=x_t-(\breve{x_t}+K_t(z_t-H\breve{x_t}))\\
&=x_t-(\breve{x_t}+K_t(Hx_t+v_t-H\breve{x_t}))\\
&=(x_t-\breve{x_t})-K_tH(x_t-\breve{x_t})-K_tv_t\\
&=(I-K_tH)(x_t-\breve{x_t})-K_tv_t
\end{align}
\]
方差公式
\[\begin{align}
\hat{\Sigma} &=E[(x_t-\hat{x_t})(x_t-\hat{x_t})^T]\\
&=E[[(I-K_tH)(x_t-\breve{x_t})-K_tv_t][(I-K_tH)(x_t-\breve{x_t})-K_tv_t]^T]\\
&=E[[(I-K_tH)\breve{e_t}-K_tv_t][\breve{e_t}^T(I-K_tH)^T-v_t^TK_t^T]]\\
&=E[(I-K_tH)\breve{e_t}\breve{e_t}^T(I-K_tH)^T-(I-K_tH)\breve{e_t}v_t^TK_t^T-K_tv_t\breve{e_t}^T(I-K_tH)^T+K_tv_tv_t^TK_t^T]\\
&中间两项E(\breve{e_t})=0,E({v_t})=0\\
&=(I-K_tH)E[\breve{e_t}\breve{e_t}^T](I-K_tH)^T+K_tE(v_tv^T_t)K^T_t\\
& 同理可知:\breve{\Sigma}=E(\breve{e_t}\breve{e_t}^T),R_t=E(v_tv^T_t)\\
&=(I-K_tH) \breve{\Sigma}(I-K_tH)^T+K_tR_tK^T_t\\
&=\breve\Sigma-K_tH\breve\Sigma-\breve\Sigma H^TK^T_t+K_tH\breve\Sigma H^TK^T+K_tR_tK^T_t\\
\tag{3}
\end{align}
\]
\(trace(\hat{\Sigma})\)的化简
\[\begin{align}
trace(\hat{\Sigma})&=trace(\breve\Sigma-K_tH\breve\Sigma-\breve\Sigma H^TK^T_t+K_tH\breve\Sigma H^TK^T+K_tR_tK^T_t)\\
&=tr(\breve{\Sigma})-2tr(K_tH\breve\Sigma)+tr(K_tH\breve\Sigma H^TK^T)+tr(K_tR_tK^T_t)
\end{align}
\]
令\(\frac{\mathrm{d}(tr(\hat\Sigma))}{\mathrm{d K_t}}=0\)
\[\frac{\mathrm{d}(tr(\hat\Sigma))}{\mathrm{d K_t}}=0-2(H \breve{\Sigma})^T+2K_tH\breve\Sigma H^T+2K_tR_t=0
\]
简化上式,卡尔曼增益$ K_t$如下
\[-(H \breve{\Sigma})^T+K_tH\breve\Sigma H^T+K_tR_t=0\\
\Downarrow\\
K_t=\breve{\Sigma}H^T(H\breve{\Sigma} H^T +R_t)^{-1}
\]
误差协方差矩阵的推导
由卡尔曼增益\(K_t\)的推导可知,其表达形式如下
\[K_t=\breve{\Sigma}H^T(H\breve{\Sigma} H^T +R_t)^{-1}
\]
它由三个参数组成,分别是 1. 先验协方差矩阵\(\breve{\Sigma}\) 2. 观测矩阵\(H\) 3. 观测噪声协方差\(R_t\)
其中2和3都是已知量,而1是未知量,因此需要推导出1的表达公式。
从定义上可知
\[\begin{align}
\breve{\Sigma} &=E[\breve{e_t}\breve{e_t}^T]\\
&=E[(x_t-\breve{x_t})(x_t-\breve{x_t})^T]
\end{align}
\]
其中
- \(x_t=Fx_{t-1}+Bu_{t}+w_{t}\)
- \(\breve{x_t}=F\hat{x_{t-1}}+Bu_{t}\)
\(\therefore x_t-\breve{x_t}=F(x_{t-1}-\hat{x_{t-1}})+w_{t}\)
代入上式
\[\begin{align}
\breve{\Sigma} &=E[[F(x_{t-1}-\hat{x_{t-1}})+w_{t}][F(x_{t-1}-\hat{x_{t-1}})+w_{t}]^T]\\
&=E[(F\hat{e}_{t-1}+w_t)(F\hat{e}_{t-1}+w_t)^T]\\
&=E[F\hat{e}_{t-1}\hat{e}^T_{t-1}F^T+F\hat{e}_{t-1}w^T_t+w_t\hat{e}^T_{t-1}F^T+w_tw_t^T]\\
&=E[F\hat{e}_{t-1}\hat{e}^T_{t-1}F^T+w_tw_t^T]\\
&=FE[\hat{e}_{t-1}\hat{e}^T_{t-1}]F^T+E[w_tw_t^T]\\
&=F\hat{\Sigma}_{t-1}F^T+Q_t
\end{align}
\]
综上,先验协方差矩阵:
\[\breve{\Sigma}=F\hat{\Sigma}_{t-1}F^T+Q_t
\]
将先验协方差矩阵代入公式(3),得到后验协方差矩阵
\[\hat{\Sigma_t}=(I-K_tH_t)\breve{\Sigma}_t
\]
工程案例
卡尔曼滤波器定位
\[\begin{align*}
&EKF\_localization\_know\_correspondences(\mu_{t-1},\Sigma_{t-1},u_t,z_t,c_t,m)\\
& \quad \theta=\mu_{t-1}.\theta\\
& \quad F_t=
\begin{bmatrix}
1 & 0 & -\frac{u_{t}.v}{u_{t}.\omega}\cos{\theta}+\frac{u_{t}.v}{u_{t}.\omega}\cos({\theta}+\omega_t \Delta{t})\\
0 & 1 & -\frac{u_{t}.v}{u_{t}.\omega}\sin{\theta}+\frac{u_{t}.v}{u_{t}.\omega}\sin({\theta}+\omega_t \Delta{t})\\
0 & 0 & 1
\end{bmatrix} \cdots \frac{\partial 运动模型}{\partial \mu}\\
& \quad B_t = \begin{bmatrix}
\frac{-\sin{\theta}+sin(\theta+\omega_t \Delta{t})}{\omega_t} &
\frac{v_t(\sin{\theta}-sin(\theta+\omega_t \Delta{t}))}{\omega_t^2}+\frac{v_t\cos({\theta}+\omega_t \Delta{t})\Delta{t}}{\omega_t}\\
\frac{\cos{\theta}-cos(\theta+\omega_t \Delta{t})}{\omega_t} &
-\frac{v_t(\cos{\theta}-cos(\theta+\omega_t \Delta{t}))}{\omega_t^2}+\frac{v_t\sin({\theta}+\omega_t \Delta{t})\Delta{t}}{\omega_t}\\
0 & \Delta{t}
\end{bmatrix} \cdots \frac{\partial 运动模型}{\partial u}\\
& \quad Q_t=\begin{bmatrix}
\alpha_1 v_t^2+\alpha_2\omega_t^2 & 0\\
o & \alpha_1 v_t^3+\alpha_4\omega_t^2
\end{bmatrix} \cdots 过程噪声\\
& \quad \breve{\mu_t}=\mu_{t-1}+
\begin{bmatrix}
-\frac{u_{t}.v}{u_{t}.\omega}\sin{\theta}+\frac{u_{t}.v}{u_{t}.\omega}\sin({\theta}+\omega_t \Delta{t})\\
\frac{u_{t}.v}{u_{t}.\omega}\cos{\theta}-\frac{u_{t}.v}{u_{t}.\omega}\cos({\theta}+\omega_t \Delta{t})\\
\omega_t \Delta{t}
\end{bmatrix} \cdots (1)运动方程 \breve{\mu_t}= F_t\mu_{t-1}+B_tu_t\\
& \quad \breve{\Sigma_t}=F_t\Sigma_{t-1}F_t^T+ B_t M_t B_t^T \cdots (2)预测估计协方差矩阵\\
& \quad R_t=\begin{bmatrix} \sigma_r^2 &0 &0\\ 0&\sigma^2_{\phi}&0 \\ 0&0&\sigma^2_{s} \end{bmatrix}\cdots 观测噪声\\
\\
& \quad for\ all \ abserved \ features \ z_t^i=(r^i_t ,\phi^i_t,s^i_t)\\
\\
& \quad \quad for \ all \ landmarks \ [k] \ in \ the \ map \ [m] \ do \\
\\
& \quad \quad \quad distance=\sqrt{(m_{k,x} - \breve{\mu}_{t,x})^2+(m_{k,y} - \breve{\mu}_{t,y})^2} \\
& \quad \quad \quad \breve{z^k_t}=\begin{bmatrix}
distance\\
atan2{\frac{m_{k,y}-\breve{\mu}_{t,y}}{m_{k,x}-\breve{\mu}_{t,x}}}-\breve{\mu}_{t}.\theta \\
m_{k,s}
\end{bmatrix} \cdots 代表H_t \breve{u_t} \\
& \quad \quad \quad H^k_t=\begin{bmatrix}
-\frac{m_{k,x}-\breve{\mu}_{t,x}}{distance} & -\frac{m_{k,y}-\breve{\mu}_{t,y}}{distance} & 0\\
\frac{m_{k,y}-\breve{\mu}_{t,y}}{distance^2}& -\frac{m_{k,x}-\breve{\mu}_{t,x}}{distance^2}&-1\\
0&0&0
\end{bmatrix}\cdots\frac{ \partial 观测方程}{\partial \mu}\\
& \quad \quad \quad S^k_t=H^k_t\breve{\Sigma_t}[H^k_t]^T+R_t \cdots 每一个匹配结果的后验协方差,即正太分布的协方差\\
& \quad \quad endfor
\\
& \quad \quad j(i)=\mathop{argmax}_k det(2\pi S^k_t)^{-\frac{1}{2}}exp^{-\frac{1}{2}(z^i_t-\breve{z^k_t})^T[S^k_t]^{-1}(z^i_t-\breve{z^k_t)}}\\
\\
& \quad \quad K^i_t=\breve{\Sigma_t}[H^j(i)_t]^T[S^{j(i)_t}]^{-1} \cdots(3)卡尔曼增益\\
\\
& \quad \quad \breve{\mu_t}=\breve{\mu_t}+K^i_t(z^i_t-z^{j(i)}_t) \cdots(4-i)后验状态估计\\
\\
& \quad \quad \breve{\Sigma_t}=(I-K^i_t H^{j(i)}_t)\breve{\Sigma_t}\cdots(5-i)后验状态估计协方差\\
\\
& \quad endfor\\
\\
& \quad \mu_t=\breve{\mu_t} \cdots(4)后验状态估计\\
& \quad \Sigma_t=\breve{\Sigma_t}\cdots(5)后验状态估计协方差\\
\\
&return \mu_t,\Sigma_t
\end{align*}
\]
符号含义:
解释:未知一致性的EKF定位,通过MLE(极大似然估计)解决corresponsedence匹配问题,即\(j(i)=k\),观测物体与map的一一对应。
卡尔曼滤波器的各种变种
这是动态系统模型
\[x_t=F_t x_{t-1}+B_tu_t+w_t\\
z_t=H_tx_t+v_t
\]
总结其特性:
- 线性
- \(F_t\):状态转换矩阵固定?
- \(w_t\)的协方差\(Q_t\):\(Q_t\)过程噪声协方差矩阵固定?
各种卡尔曼衍生方法的应用范围
- 若状态转换过程确定,且被估计的过程和观测变量与过程的关系是线性的,则可以直接应用卡尔曼滤波;
- 若状态转换过程确定,且被估计的过程和观测变量与过程的关系是非线性的,则应该使用扩展卡尔曼滤波;
- 若状态转换过程不确定,且关于过程的信息量少,则应该使用灰色卡尔曼滤波;
- 若状态转换过程不确定,但可以获得大量过程信息,则应该使用交互式多模型方法;
- 若状态转换过程是随时间变化的,则应该使用自适应卡尔曼滤波方法。
变种简称说明
- ekf:扩展卡尔曼滤波
- eskf:Error-State卡尔曼滤波
- ukf:unscented kalman filter无迹卡尔曼滤波
- ckf:cubature Kalman filter容积卡尔曼滤波
- qkf: quadrature Kalman filter 正交卡尔曼滤波器
- cqkf:容积求积卡尔曼滤波
- srukf:平方根卡尔曼滤波
- quadratic kalman filter:二次卡尔曼滤波器
- dual kalman filter:双卡尔曼滤波器
- adaptive kalman filter:自适应卡尔曼滤波
- multi-rate kalman filter:多速率卡尔曼滤波器
- indirect kalman filter:间接卡尔曼滤波器
扩展卡尔曼滤波公式(EKF)
核心思想
使用泰勒级数将非线性函数局部线性化
动态系统
\[\breve{x_t}=f(x_{t-1},u_t)+w_t\\
z_t=h(x_t)+v_t
\]
EKF公式
预测
\[\breve{x_t}=f(x_{t-1},u_t)\\
\breve{\Sigma}_t=F_t \Sigma_{t-1} F_t^T+ Q_t
\]
卡尔曼增益
\[K_t=\breve{\Sigma_t}H_t^T(H_t\breve{\Sigma_t}H_t^T+R_t)^{-1}
\]
更新
\[\hat{x_t}=\breve{x_t}+K_t(z_t-h(\breve{x_t}))\\
\hat{\Sigma}_t=(I-K_tH_t)\breve{\Sigma}_t
\]
其中\(F_t=jacobian(f)\),\(H_t=jacobian(h)\)
无迹卡尔曼滤波(UKF)
核心思想
通过使用加权统计线性回归过程实现随机线性化
公式
\[\begin{align}
& Algorithm \ UKF(\mu_{t-1},\Sigma_{t-1},u_{t},z_{t})\\
& \quad 根据状态量的维度n,分布sigma点\\
& \quad \chi_{t-1}=\begin{bmatrix}\mu_{t-1} & \mu_{t-1}+\sqrt{(n+\lambda)\Sigma_{t-1}} & \mu_{t-1}-\sqrt{(n+\lambda)\Sigma_{t-1}} \end{bmatrix} \\
% sigma的先验数据
& \quad \breve\chi^*_t=g(u_t,\chi_{t-1})\\
% 状态预测
& \quad \breve{\mu}_t=\sum^{2n}_{i=0}w^{[i]}_m \breve\chi^{*[i]}_t \\
\\
& \quad 先验协方差\\
& \quad \breve{\Sigma_t}=\sum^{2n}_{i=0}w^{[i]}_c(\breve{\chi}^{*[i]}_t-\breve{\mu}_t)(\breve{\chi}^{*[i]}_t-\breve{\mu}_t)^T+Q_t\\
\\
& \quad 先验观测量的sigma点分布\\
& \quad \breve{\chi}_t=\begin{bmatrix}\mu_{t} & \mu_{t}+\sqrt{(n+\lambda)\breve{\Sigma}_{t}} & \mu_{t}-\sqrt{(n+\lambda)\breve{\Sigma}_{t}} \end{bmatrix} \\
& \quad \breve{Z_t}=h(\breve{\chi}_t)\\
& \quad \breve{z}_t=\sum^{2n}_{i=0}w^{[i]}_m \breve Z^{*[i]}_t\\
\\
& \quad 卡尔曼增益\\
& \quad S_t=\sum^{2n}_{i=0}w^{[i]}_c(\breve{Z}^{*[i]}_t-\breve{z}_t)(\breve{Z}^{*[i]}_t-\breve{z}_t)^T+R_t\\
& \quad \breve{\Sigma}^{x,z}_t=\sum^{2n}_{i=0}w^{[i]}_c(\breve{\chi}^{[i]}_t-\breve{\mu}_t)(\breve{Z}^{[i]}_t-\breve{z}_t)^T \\
& \quad K_t= \breve{\Sigma}^{x,z}_t S_t^{-1}\\
\\
& \quad 更新\\
& \quad \mu_t =\breve{\mu}_t + K_t(z_t-\breve{z_t}) \\
& \quad \Sigma=\breve{\Sigma}_t-K_t S_t K_t^T \\
&return \ \mu_t,\Sigma_t
\end{align}
\]
符号释义
\(\chi=\begin{bmatrix} x_1 & x_1+(\sqrt{(n+\lambda)\Sigma})_i\cdots i=1,\cdots,n & x_1-(\sqrt{(n+\lambda)\Sigma})_{i-n}\cdots i=n+1,\cdots,2n\\ x_2 & x_2+(\sqrt{(n+\lambda)\Sigma})_i & x_2-(\sqrt{(n+\lambda)\Sigma})_{i-n}\\ \vdots&&\\x_n & x_n+(\sqrt{(n+\lambda)\Sigma})_i & x_n-(\sqrt{(n+\lambda)\Sigma})_{i-n} \end{bmatrix}\)
均值权重
\(w^{[i]}_{m}=\begin{cases} \frac{\lambda}{n+\lambda},当i=0 \\ \frac{1}{2(n+\lambda)},当i=1,\cdots,2n\end{cases}\)
协方差权重
\(w^{[i]}_{c}=\begin{cases} \frac{\lambda}{n+\lambda}+(1-\alpha^2+\beta),当i=0 \\ \frac{1}{2(n+\lambda)},当i=1,\cdots,2n\end{cases}\)
参考
[1] 卡尔曼滤波 - 维基百科,自由的百科全书 (wikipedia.org)
[2] B站 DR_CAN 卡尔曼滤波器视频
[3] <<机器人学中的状态估计>>--Timothy D. Barfoot著
[4] 王学斌,徐建宏,张章.卡尔曼滤波器参数分析与应用方法研究[J].计算机应用与软件,2012,29(06):212-215.
[5] 自动驾驶感知融合-无迹卡尔曼滤波(Lidar&Radar) - 知乎 (zhihu.com)
[6] 《概率机器人》-Sebastian Thrun , Wolfram Burgard, Dieter Fox著






 浙公网安备 33010602011771号
浙公网安备 33010602011771号