底盘结构
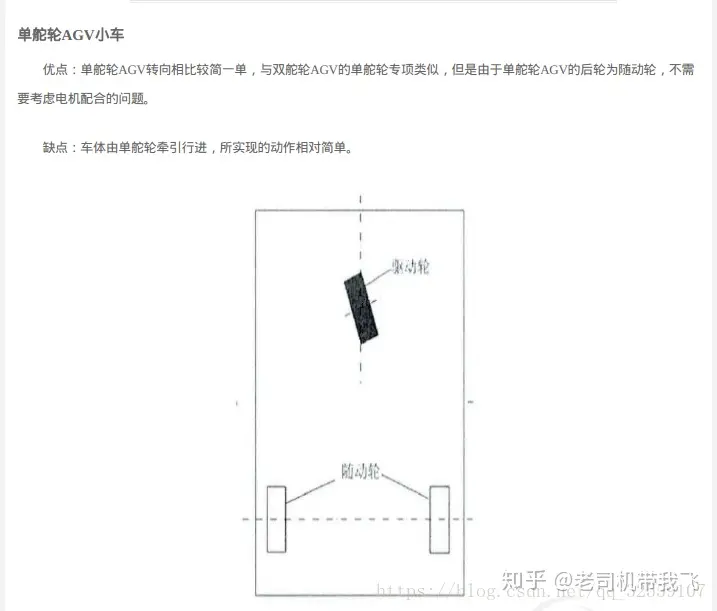
驱动轮的作用:驱动轮,转向轮。
随动轮的作用:仅仅支撑车体。
选取车体坐标系
选取从动轮轴心的连线中点M(X,Y)为车体坐标系(body frame)的原点
运动模型
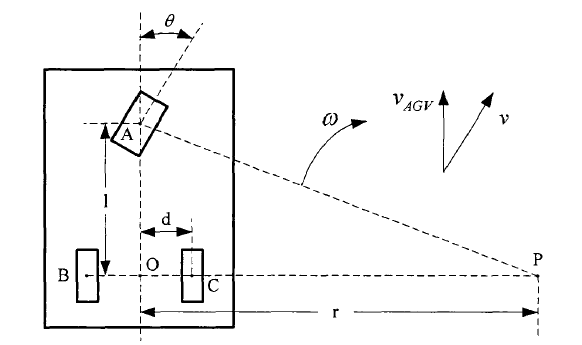
上图是单舵轮车体在世界坐标系下的示意图,其中M(X,Y)与\(\theta\)组成车体的位姿\((x_{car},y_{car},\theta_{car})\)。
\(\nu\)代表单舵轮的线速度,\(\theta\)代表舵机轮的偏向角,r为车体做圆周运动的半径。
设控制量u为(\(v、\theta\)),输出为(\(v_{AGV},\omega_{AGV}\))。
求取(\(v_{AGV},\omega_{AGV}\))与的(\(v、\theta\))关系?
问题
公式推导
符号定义
推导过程
从图中得知
\[\theta=\angle APO\\
v_{AGV}=v*cos(\theta)
\]
"半径为AP的圆周运动"与"半径为OP的圆周运动"的关系为:
\[AP\times cos(\theta)=OP\\
AP=\frac{l}{sin\theta}
\]
所以
\[OP=r=\frac{l}{ tan(\theta)}
\]
同理,已知A点的舵轮的角速度\(\omega\)
\[\omega_{AGV}=\omega*cos(\theta)
\]
又已知
\[\omega= \dot{\theta}= \frac{v} {\frac{l}{sin\theta}}
\]
综上
\[v_{AGV}=v*cos(\theta) \\
\omega_{AGV}=\frac{v_{AGV}}{r}=\frac{v_{AGV}*tan(\theta)}{l}=\frac{v*sin{\theta}}{l}\\
\]
结论
正向解
\[v_{AGV}=v*cos{\theta} \\
\omega_{AGV}=\frac{v*sin{\theta}}{l}\\
\]
逆向解
\[\theta=arctan(\frac{l}{\frac{v_{AGV}}{\omega_{AGV}}})\\
v=\frac{v_{AGV}}{cos{\theta}}
\]
参考
[1]曹杰华. 单舵轮AGV路径跟踪控制方法的研究[D].广东工业大学,2021.DOI:10.27029/d.cnki.ggdgu.2021.002146.
[2]范堃. 自动导引车车载系统研究与实现[D].浙江大学,2013.




