差分轮底盘模型
轮式机器人的运动模型作用
当输入\((v_{car},\omega_{car})\),可以推出所有轮式机器人的电机的转速\(\Phi\),即运动模型的逆向解
底盘的结构

选取车体坐标系
运动模型
问题
两轮差分底盘如上图所示(图片来自网络),它有两个驱动轮和一些万向轮,驱动轮的作用是控制车体行走,万向轮的作用是支撑车体底盘。
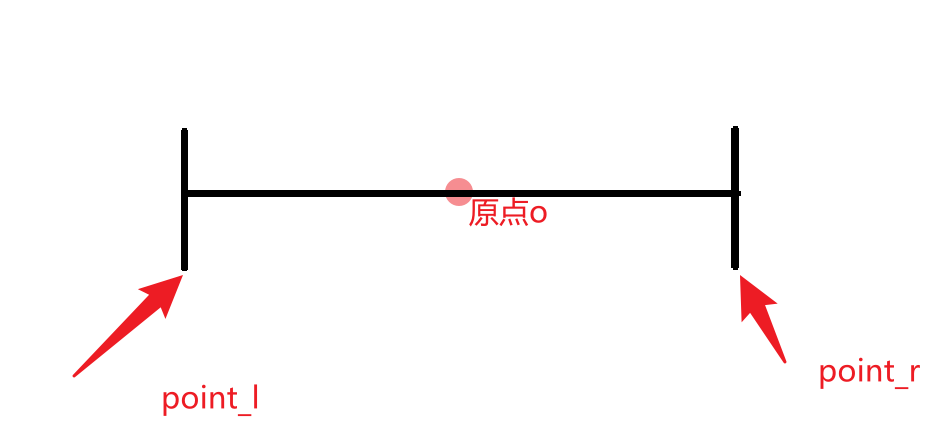
现在我们设车体模型为一个刚体,左右两个驱动轮接触地面的接触点为 point_l、point_r,两点连线的中点为\(o\),即车体坐标系(\(body Frame\))的原点
求取车体(原点\(o\))的移动线速度与角速度(\(v_{car}、\omega_{car}\))与左右驱动电机的转速(\(\Phi_r、\Phi_l\))的公式关系?
公式推导
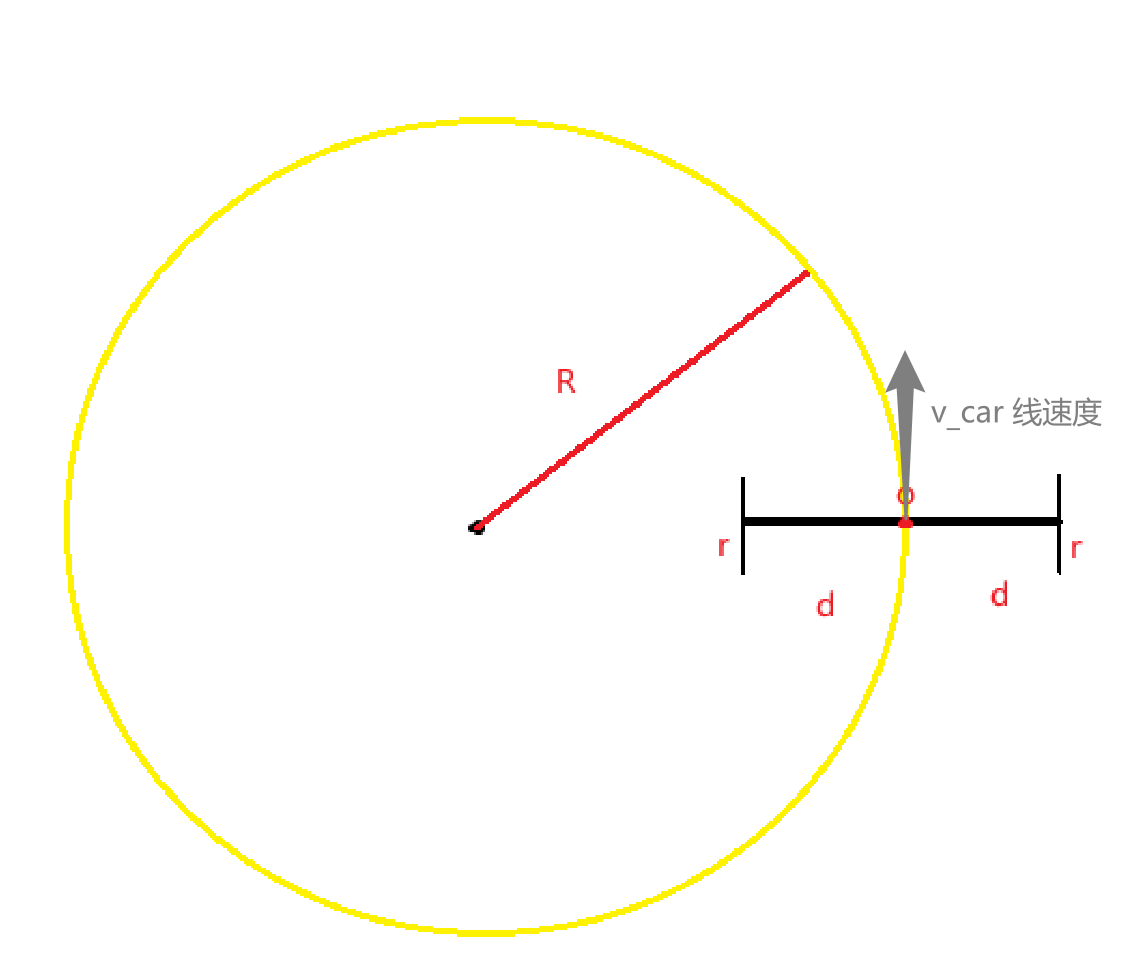
圆弧运动
由于差分底盘的运动特性,它仅能进行圆弧运动,R为圆弧运动的半径,但是在正常行走过程中,直线运动是不可避免的,如何表示直线运动呢?
当R=\(\infty\),车体直线运动。
当R=0,车体原点旋转。
符号含义
- 驱动轮的左轮和右轮的线速度(\(v_l,v_r\))
- 驱动轮的左轮和右轮的电动转速(\(\Phi_l、\Phi_r\))
- 驱动轮的左轮和右轮的角速度(\(\omega_l,\omega_r\))
- 两轮之间的距离(轮间距): \(2d\)
- 驱动轮的轮子半径: \(r_{wheel}\)
- 圆弧运动的半径R
- 车体的线速度和角速度(\(v_{car}、\omega_{car}\))
推导
已知,“电机的转速运动” 与 “差分轮的圆周运动” 有如下关系:
\[v_l=(R-d)*\omega_l=\Phi_l*2\pi r_{wheel} \\
v_r=(R+d)*\omega_r=\Phi_r*2\pi r_{wheel} \tag{1}
\]
由上可得,公式(1)可推导出公式(2)(3)(4)
驱动轮的角速度方程
\[\omega_l=\frac{v_l}{(R-d)}\\
\omega_r=\frac{v_r}{(R+d)} \tag{2}
\]
当做圆周运动时,左右驱动轮的角速度相等,即$\omega_r=\omega_l $
\[\frac{v_l}{R-d}=\frac{v_r}{R+d} \tag{3}
\]
所以运动圆弧半径R为
\[R=\frac{(v_r+v_l)*d}{v_r-v_l} \tag{4}
\]
根据(4)可得
\[R+d=\frac{(v_r+v_l)*d}{vr-vl}+d=\frac{(v_r+v_l)*d}{vr-vl}+\frac{(v_r-vl)*d}{(v_r-v_d)}=\frac{2v_r*d}{v_r-v_l} \tag{5}
\]
所以 ,将角速度\(\omega_{car}\)和线速度\(v_{car}\)用\(v_r,v_l\)表示:
由于底盘中心角速度\(\omega_{car}=\omega_l=\omega_r\),所以将(5)代入。
得到角速度方程\(\omega_{car}\)
\[\omega_{car}=\omega_r=\frac{v_r} {R+d}=\frac{v_r-v_l}{2d} \tag{6}
\]
底盘中心线速度\(v_{car}\)
\[v_{car}=\omega_r*R=\omega_l*R \\
v_{car}=\frac{v_l+v_r}{2} \tag{7}
\]
结论
运动模型正解
(input:\(v_l,v_r\)或\(\Phi_l,\Phi_r\);output:\(v_{car} \omega_{car}\))
\[R=\frac{(v_r+v_l)*d}{v_r-v_l}=\frac{(\Phi_r+\Phi_l)*d}{\Phi_r-\Phi_l}\\
v_{car}=\frac{v_l+v_r}{2}=\pi r_{wheel}(\Phi_l+\Phi_r)\\
\omega_{car}=\frac{v_r-v_l}{2d}=\frac{\pi r_{wheel}(\Phi_r-\Phi_l)}{d}
\]
矩阵化
\[\begin{bmatrix}
v_{car}\\
\omega_{car}
\end{bmatrix}
=
\begin{bmatrix}
\frac{1}{2} & \frac{1}{2}\\
\frac{-1}{2d} & \frac{1}{2d}
\end{bmatrix}
\begin{bmatrix}
v_l\\
v_r
\end{bmatrix}
=
\begin{bmatrix}
\frac{1}{2} & \frac{1}{2}\\
\frac{-1}{2d} & \frac{1}{2d}
\end{bmatrix}
\begin{bmatrix}
2\pi r_{wheel}*\Phi_l\\
2\pi r_{wheel}*\Phi_r
\end{bmatrix}
\]
运动模型逆解
(input: \(v_{car} \omega_{car}\);output:\(v_l,v_r\)或\(\Phi_l,\Phi_r\))
\[R=\frac{v_{car}}{\omega_{car}}\\
v_l=(R-d)*\omega_{car}\\
v_r=(R+d)*\omega_{car}
\]
扩展可得
\[2\pi r_{wheel}*\Phi_l=(\frac{v_{car}}{\omega_{car}}-d)*\omega_{car}\\
2\pi r_{wheel}*\Phi_r=(\frac{v_{car}}{\omega_{car}}+d)*\omega_{car}\\
\]
矩阵化
\[\begin{bmatrix}
v_l\\
v_r
\end{bmatrix}
=
\begin{bmatrix}
2\pi r_{wheel}*\Phi_l\\
2\pi r_{wheel}*\Phi_r
\end{bmatrix}
=
\begin{bmatrix}
1 & -d\\
1 & d
\end{bmatrix}
\begin{bmatrix}
v_{car} \\
\omega_{car}
\end{bmatrix}
\]





