DS博客作业03--树
0.PTA总分

1.本周学习总结
1.1 总结树及串内容
串
- 串的BF算法
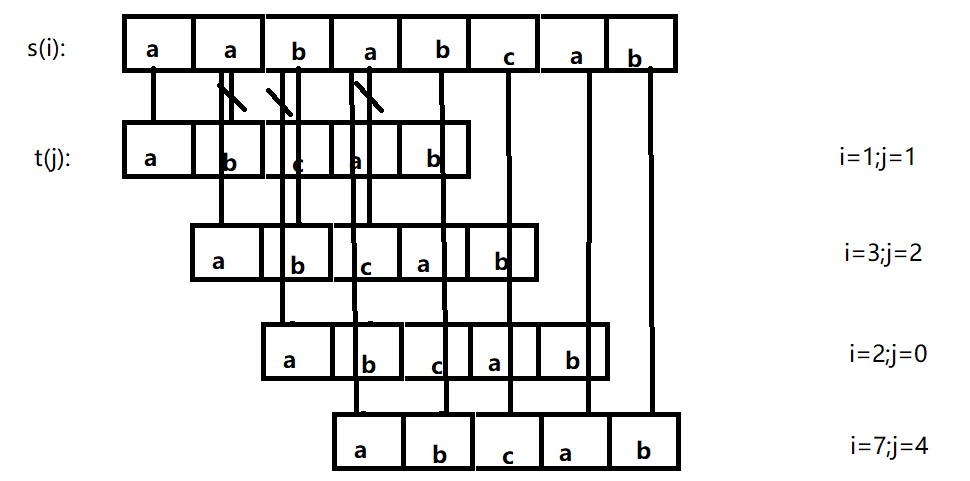
BF算法通俗来讲就是暴力算法。
其暴力的手法:每当匹配失败时,母串从本次匹配开始位置的后一位开始匹配,子串从头开始继续匹配,直到子串匹配完成才算成功。
当母串长度为m,子串长度为n时,其最坏情况下(母串中无匹配子串),时间复杂度达O(m*n),最好情况下(母串第一位开始就是子串)只有O(1)。
int BF(char s[],char t[])
{
int i=0;
int j=0;
while((i<strlen(s))&&(j<strlen(t))) //当下标超过数组长度时,查找完成
{
if(s[i]==p[j])
{
i++;
j++;
}
else
{
i=i-j+1; //母串回到前一次匹配后一位
j=0; //子串回0
}
}
if(j==strlen(p)) //若子串遍历完成,说明匹配成功
{
return i-j+1; //返回子串在母串第一次出现的位置
}
else
{
return -1;
}
}
- 串的KMP算法
KMP算法,其实我也只是知道如何去实现,但其中具体的思想还是没整太明白。
区别于BF的地方:每次匹配失败后,主串的下标i并不会像BF算法一样回退,而是移动子串到母串相应位置即可。
其中重要的是引入next数组,该数组保存子串第j位前的字符串的最长匹配的前缀后缀
母串长度m,子串长度n时,时间复杂度O(m+n)。

next数组:对于abab来说,第4个字符b之前的字符串aba中,第一个a跟最后一个a匹配且长度为1,所以next[3]值为1.由如abcabd,第6个字符d前字符串:abcab,含有 ‘前ab’==‘后ab’,长度为2,所以next[5]=2。

求next数组
void GetNext(SqString t,int next[])
{
int j, k;
j=0; k=-1;
next[0|=-l;
while (j<t.length-l)
{
if (k=-l || t.data[j]=t.data[kl)
{
j++; k++;
next[j]=k;
}
else k=next[k];
}
}
KMP算法
int KMPIndex(SqString s,SqString t)
{
int next[MaxSize],i=0,j=0;
GetNext(t,next);
while (i<s.length && j<t.length)
{
if (j==-l || s.data[i]==t.data[j])
{
i++ ;
j++; //i,j 各增 1
}
else j=next[j] ; //i不变,j后退
}
if (j>=t.length)
return (i-t. length) ;//匹配模式串首字符下标
else
return -1;//返回不匹配标志
}
二叉树
二叉树,顾名思义,树的每个结点最多有两个分支,当然也可以只有一个或没有。两个分支根据位置被称作“左子树”和“右子树”。
满二叉树:可以说是二叉树的理想情况。通俗来说,就是每个结点都有两个子树;转化为数学而言:一棵深度为k的满二叉树,具有的结点数为(2^k)-1
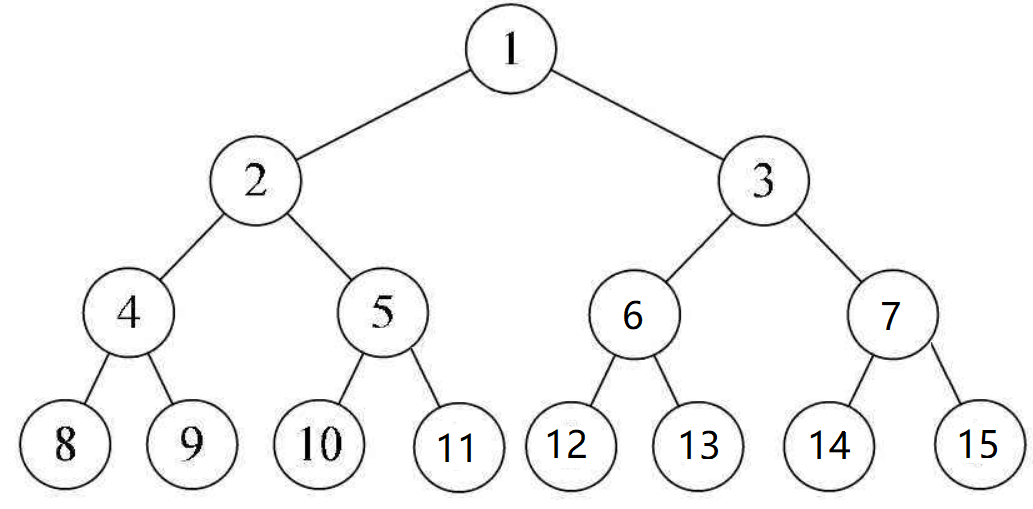
完全二叉树:满二叉树则是完全二叉树的一种特殊情况。完全二叉树当从上往下,从左往右遍历时,不能有空结点。在最后一层可以不满
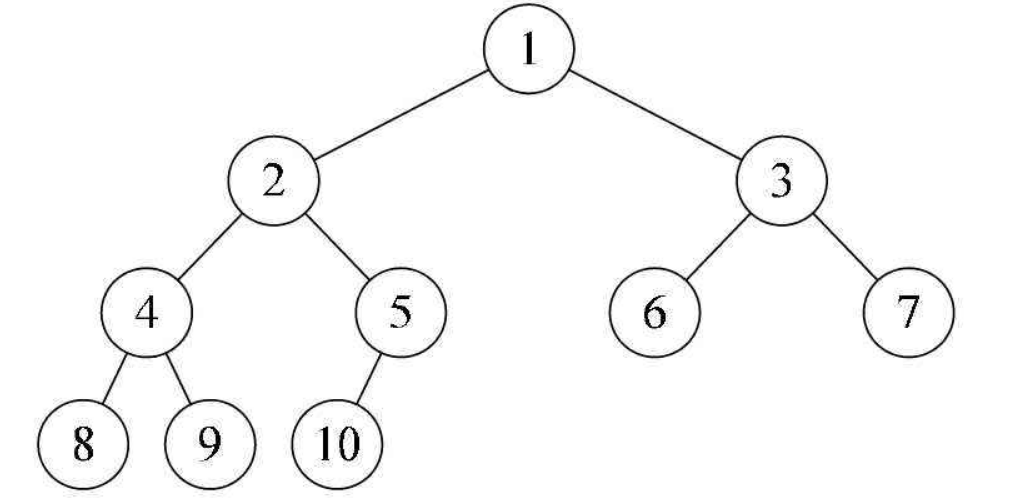
- 存储结构
-
顺序存储

从下标1开始存储具有性质:
1.非根结点i的父结点序号为[i/2]
2.结点i的左孩子序号为2i
3.结点i的右孩子序号为2i+1
不足之处:当树的数据较为极端时,采用顺序存储会造成空间的浪费。数组通病:不便于插入,删除

-
链式结构
二叉树结点由一个数据元素和分别指向其左、右子树和两个分支构成
表示二叉树的链表中的结点至少包含3个域:数据域和左、右指针域(lchild,rchild)
typedef struct BTNode
{
ElemType data;
struct BTNode *lchild, rchild;
}BTNode,BTree;

- 二叉树建法
- 顺序转二叉链
len=str.length();
BTree CreateBTree(string str,int i)//下标从1开始
{
int len;
BTree t;
t=new BTNode;
if(i>len || i<=0||str[i]=='#') return NULL;
t->data =str[i];
t->lchild =CreateBTree(str,2*i); //左子树
t->rchild =CreateBTree(str,2*i+1); //右子树
return t;
}
- 先序串转二叉链
void CreateBiTree(BiTree& T,string s)
{
char ch;
ch=s[i++];
if (ch == '#') T = NULL;
else
{
T = new BiTNode;
T->data = ch;
CreateBiTree(T->lchild,s);
CreateBiTree(T->rchild,s);
}
}
3.层次法建树
void CreateBiTree(BTree& BT, string s)//以#开头的字符串
{
int i = 1;
BTree T;
queue<BTree>Q;
if (s[1] != '#')
{
BT = new BtNode;
BT->data = s[1];
BT->lchild = BT->rchild = NULL;
Q.push(BT);
}
else BT = NULL; //首个字符非空时入队列,否则为空链
while (!Q.empty() && i < len-1)
{
T = Q.front();
Q.pop();
i++;
if (s[i] == '#')
{
T->lchild = NULL;
}
else //左孩子非空时入队
{
T->lchild = new BtNode;
T->lchild->data = s[i];
T->lchild->lchild = T->lchild->rchild = NULL;
Q.push(T->lchild);
}
i++;
if (s[i] == '#')
{
T->rchild = NULL;
}
else //右孩子非空时入队
{
T->rchild = new BtNode;
T->rchild->data = s[i];
T->rchild->lchild = T->rchild->rchild = NULL;
Q.push(T->rchild);
}
}
}
- 二叉树遍历
- 先序遍历
void PreorderPrintLeaves( BinTree BT )
{
if(BT) //节点非空时进入
{
if(BT->Left==NULL&&BT->Right==NULL)//节点左右子树均空时进入
{
printf(" ");
printf("%c",BT->Data);
}
PreorderPrintLeaves( BT->Left ); //先遍历左子树
PreorderPrintLeaves( BT->Right ); //遍历右子树
}
}
- 中序遍历
void InorderPrintNodes( BiTree T)
{
if(T)
{
InorderPrintNodes(T->lchild);
printf(" %c",T->data);
InorderPrintNodes(T->rchild);
}
}
- 后续遍历
void PostOrder(BTree T)
{
if (T)
{
PostOrder(T->lchild);
PostOrder(T->rchild);
printf("%c ",T->data);
}
}
- 层次遍历
void levelOrder(BTree root)//层序遍历
{
int flag=1; //空格输出控制
queue<BTree> que;
if (root == NULL || len == 1) //由于是以'#'开始,长度为1 时也为空
{
cout << "NULL";
return;
}
que.push(root); //入队根节点
while (!que.empty()) //队列非空时
{
BtNode* front = que.front();
que.pop();
if(flag==1)
{
cout << front->data;
flag=0;
}
else cout << " " << front->data; //输出队头元素且出队
if (front->lchild) que.push(front->lchild);
if (front->rchild) que.push(front->rchild); //左孩子或右孩子非空时入队
}
}
树
- 树的存储结构
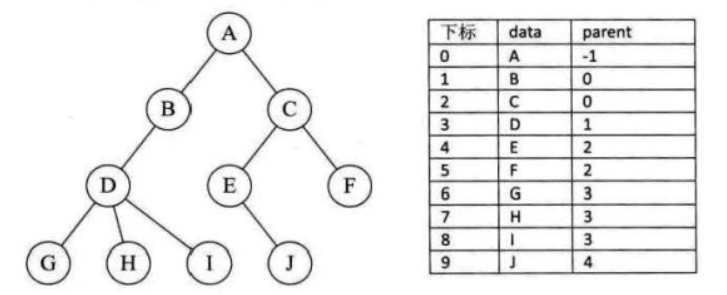
1.双亲表示法
结构中至少包含data,parent(指向父亲)
优势:找父亲容易;不足:找孩子不容易。
typedef struct
{
ElemType data;
int parent;
} Tree[MaxSize];
typedef struct TSnode
{
ElemType data;
struct TSnode *child[MaxSons];
} TNode;

- 孩子兄弟链存储结构
优势:可以表示结构较复杂的树,且很好的利用空间
缺陷:找父亲不容易。可添加parent指针解决。
typedef struct Tnode
{
ElemType data; //结点的值
struct Tnode *son; //指向兄弟
struct Tnode *brother; //指向孩子结点
} TSBNode;

- 树的操作
操作中最普遍的还为:遍历、插入、删除。
- 遍历
-
先序遍历

-
后续遍历
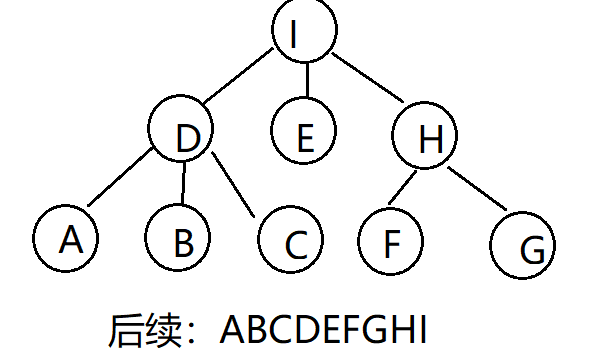
-
层次遍历

- 插入、删除(跟链表操作大同小异)

-
树的应用
典型的属哈夫曼树及哈夫曼树编码、线索二叉树、并查集等。 -
线索二叉树
普通二叉树中,会有不少的空节点,如何将这些空节点利用起来,就是线索二叉树的作用。
其结构体中增加了ltag跟rtag两项,作为是否有孩子的标值
其中: -
ltag为0时lchild指向该结点的左孩子,为1时lchild指向该结点的前驱;
-
rtag为0时rchlid指向该结点的右孩子,为1时rchlid指向该结点的后继;
typedef struct TNode
{
ElemType data; //结点数据
struct BTNode *lchild, *rchild; //左右孩子指针
int ltag; //左右标志
int rtal;
}BTNode, *BTree;
以下图为例,展示3种线索二叉树:

-
先序线索二叉树
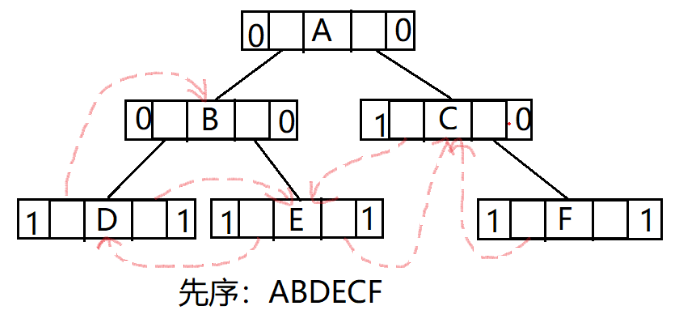
-
中序线索二叉树

-
后序线索二叉树
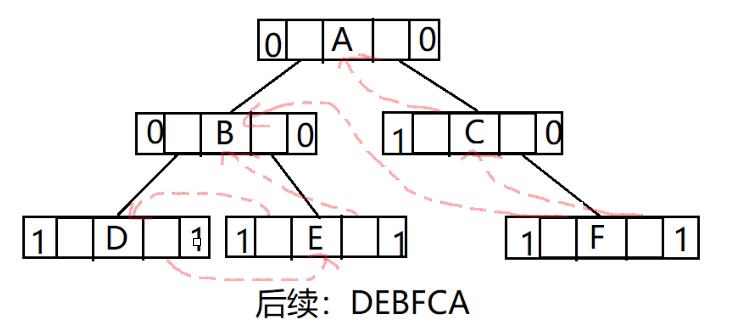
- 哈夫曼树、哈夫曼编码
哈夫曼树又称最优树,是一类带权路径长度最短的树。
树的带权路径长度指的是树中所有叶子结点的带权路径长之和。(wpl值)
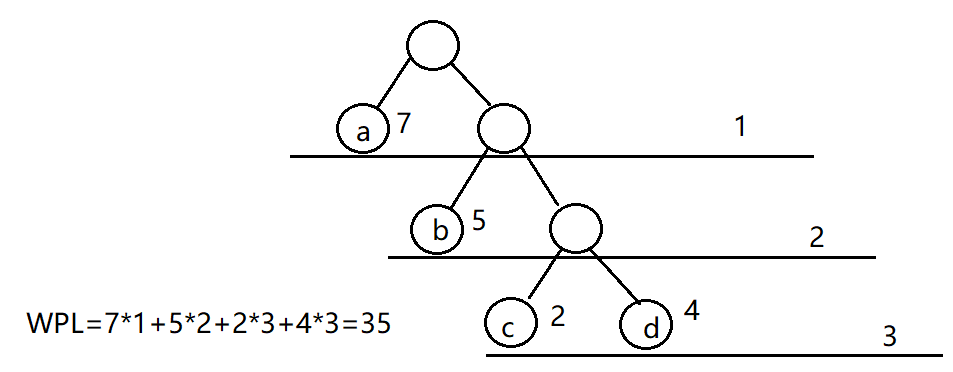
哈夫曼树构建
简单来讲就是每次取两个最小值进行建树,树的结点为两个孩子之和。
typedef struct
{
int data;
double weight;
int parent;
int lchild;
int rchild;
}HTNode;
void CreateHt(HTNode ht[], int n)
{
int i, j, k;
int lnode, rnode;
int min1, min2;
for (i = n; i < 2 * n - 1; i++)
{
min1 = min2 = 100000000; //初始化min值,防止样例值过大
//min1最小值,min2次小值
lnode = rnode = -1;
ht[i].parent = -1; //初始化结点
for (k = 0; k < i ; k++)
{
if (ht[k].parent == -1) //当结点无parent时进行,有parent说明结点已是某一结点的左(右)子树
{
if (ht[k].data < min1) //找最小值min1,使得左子树为min1
{
min2 = min1;
rnode = lnode;
min1 = ht[k].data;
lnode = k;
}
else if(ht[k].data < min2) //找次小值min2,使得右子树为min2
{
min2 = ht[k].data;
rnode = k;
}
}
}
ht[lnode].parent = i;
ht[rnode].parent = i;
ht[i].data = ht[lnode].data + ht[rnode].data;
ht[i].lchild = lnode;
ht[i].rchild = rnode; //构建parent结点,并指向对应的左右子树。
}
}
- 哈夫曼树编码
哈夫曼树编码简单来看是在原有的哈夫曼树基础上,将每个结点左孩子的权值改为0,右孩子权值改为1。
其主要用于通信方面传输问题
对于一段文字如:BADCADFEED;用二进制传输。
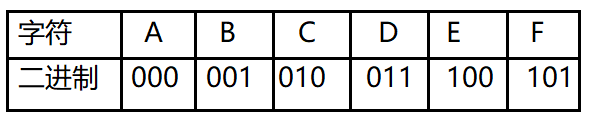
传输的数据为 “001000011010000011101100100011”
当传输一篇文章时,可想长度的可怕。
由于文本中每个字符的出现频率相加必为1,所以我们用频率作为权值进行建树。之后再更改权值为0或1。
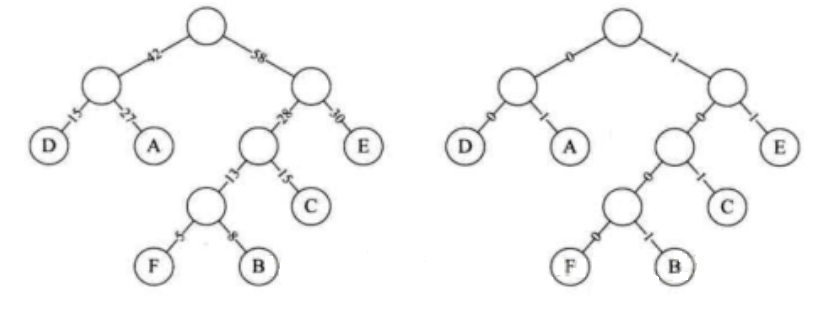
我们得到新的字符表
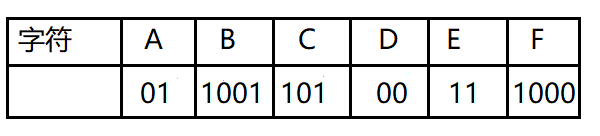
以及新的数据报:1001010010101001000111100
相对于旧的数据:001000011010000011101100100011
可见数据被压缩了,在传输大量文本时可节约不少的传输成本。
- 并查集
之前网上冲浪时发现了一个跟并查集相关且较有趣的故事,这里进行摘抄转载。原文链接
江湖上散落着各式各样的大侠,有上千个之多。他们没有什么正当职业,整天背着剑在外面走来走去,碰到和自己不是一路人的,就免不了要打一架。但大侠们有一个优点就是讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。这样一来,江湖上就形成了一个一个的帮派,通过两两之间的朋友关系串联起来。而不在同一个帮派的人,无论如何都无法通过朋友关系连起来,于是就可以放心往死了打。但是两个原本互不相识的人,如何判断是否属于一个朋友圈呢?
我们可以在每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物。这样,每个圈子就可以这样命名“中国同胞队”美国同胞队”……两人只要互相对一下自己的队长是不是同一个人,就可以确定敌友关系了。
但是还有问题啊,大侠们只知道自己直接的朋友是谁,很多人压根就不认识队长抓狂要判断自己的队长是谁,只能漫无目的的通过朋友的朋友关系问下去:“你是不是队长?你是不是队长?”这样,想打一架得先问个几十年,饿都饿死了,受不了。这样一来,队长面子上也挂不住了,不仅效率太低,还有可能陷入无限循环中。于是队长下令,重新组队。队内所有人实行分等级制度,形成树状结构,我队长就是根节点,下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候,只要一层层向上问,直到最高层,就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否是一个帮派的,至于他们是如何通过朋友关系相关联的,以及每个圈子内部的结构是怎样的,甚至队长是谁,都不重要了。所以我们可以放任队长随意重新组队,只要不搞错敌友关系就好了。于是,门派产生了。
结构体
typedef struct TREE
{
Elemtype data; //数据
int parent; //双亲下标
int rank; //结点秩
}UNode;
初始化
void init(UNode T[], int n)
{
int i = 1;
for (i = 1; i <= n; i++)
{
T[i].data=i;
T[i].parent = i;
T[i].rank = 0;
}
}
查找元素所属的集合
int find(UNode T[], int x)
{
if (x != T[x].parent)
{
return find(T, T[x].parent); //递归找双亲,直到根(boss)。
}
else return x;
}
合并集合
void Union(UNode T[], int x, int y)
{
int a, b;
Ux = find(T, x); //Ux为x的"boss";Uy为y的"boss"
Uy = find(T, y);
if (T[Ux].rank>=T[b].rank) //秩小的合并到秩大的"下属"
{
T[Uy].parent = Ux;
}
else
{
T[Ux].parent = Uy;
}
}
1.2 谈谈你对树的认识及学习体会。
整个学下来,感觉有复杂有简单,但总体而言,个人还是觉得较难。尤其是每个题目中如何定义正确的结构体,如何使用结构体,以及如何创建对应结构体的树,这些我觉得是最为需要攻克的难题。一道题的难易、编写代码复杂与否等往往与结构体相关。在写PTA中一些题目的时候,往往是想思路最难,编写过程以及调试最花时间,所以今后要熟悉结构体对数据的掌握。
2.阅读代码
2.1 1379. 找出克隆二叉树中的相同节点
代码
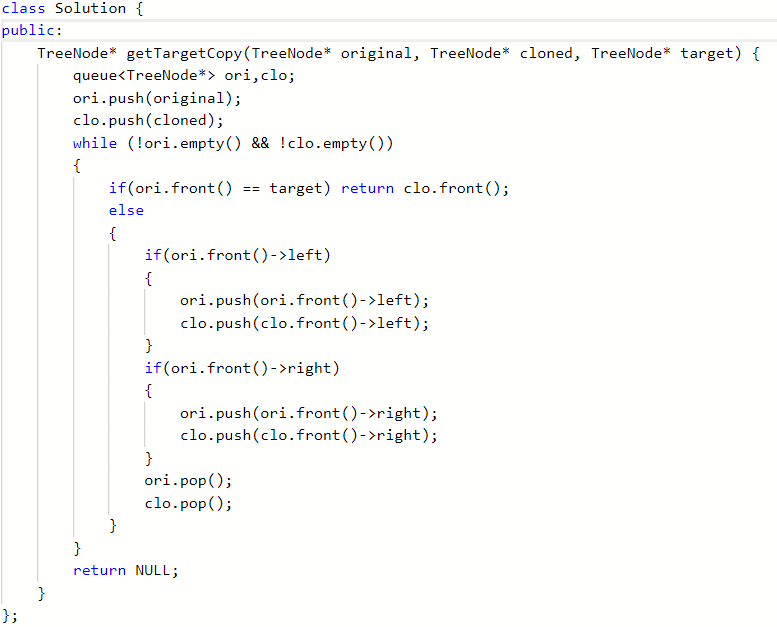
2.1.1 该题的设计思路
思路不难,两棵树同时进行层次遍历,然后原树匹配成功的时候,克隆树也就成功了,返回克隆树当前所在结点。
2.1.2 该题的伪代码
TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target)
{
定义ori,clo队列;
两棵树同步操作:
入栈根节点push;
while(两队列均不空时)
{
if(ori队头元素值跟目标值相等)return 克隆树队头结点;
左、右边孩子非空时 左、右孩子入队push;
队头出队pop
}end while
循环结束仍没返回结点说明匹配失败,return NULL;
}
2.1.3 运行结果

2.1.4分析该题目解题优势及难点。
优势:提供了同步操作的思路,我刚开始想的时候是想记录ori树寻找目标值的路径,再将路径放到clo树上。对比之下显得有些麻烦。
难点:若是直接匹配元素值是否相等的话,若树中本身就有相同元素会造成匹配错误。
2.2 面试题32 - III. 从上到下打印二叉树 III
代码

2.2.1 该题的设计思路
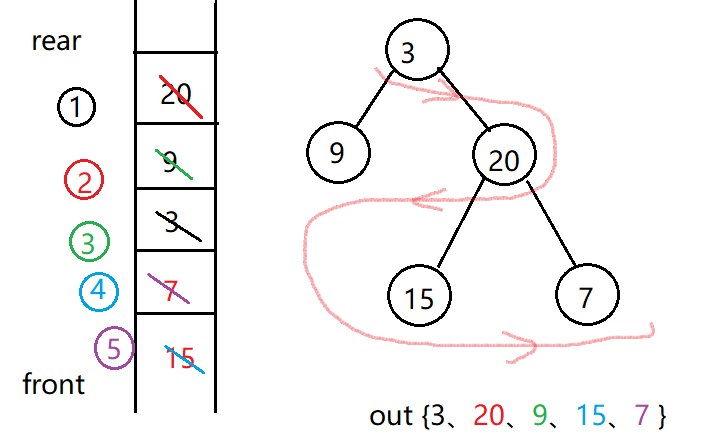
采用双端队列,层次遍历的变形。树的奇数层采取前取后放,偶数层采取后取前放。
2.2.2 该题的伪代码
while(队列非空时)
{
while(遍历当前层)
{
if(层数为奇数)
{
取队头元素;
队头出队;
左、右孩子非空时,左、右孩子入队队尾;
}
else
{
取队尾元素;
队尾出队;
右、左孩子非空时,右、左孩子入队队尾;//注意先右后左;
}
}
}
2.2.3 运行结果

2.2.4分析该题目解题优势及难点
优势:采用双端队列可以较好的简化题目,只需将平常的层序遍历反向编写即可。
难点:直接判断层数的奇偶并不容易,所以用flag变量来记录是正序入队还是反序入队。另外反序入队时,是先右孩子再左孩子。
2.3 1145. 二叉树着色游戏
代码

2.3.1 该题的设计思路
求出x所在结点的左分支,右分支以及连结父亲的分支各有多少节点数,只要任一结点数大于(n+1)/2,则存在。
2.3.2 该题的伪代码
先序遍历树,直到x结点;
left=GetSum(x->lchild);//遍历x结点左子树
right=GetSum(x->rchild);//遍历x结点右子树
连接父亲分支结点数father即为总数-left-right;
if(三者任一者大等于(n+1)/2)retrun true;
2.3.3 运行结果
2.3.4分析该题目解题优势及难点
优势:将看似难处理的题目,通过数学理解转化为简单的分支结点求和。
难点:难处就在于能不能看出这个数学问题,当然我刚开始是没有想到的。
2.3 450. 删除二叉搜索树中的节点
代码

2.3.1 该题的设计思路
所要删除的结点有三种情况:
- 所删除结点为叶子结点,可以直接删除。
- 所删除结点拥有右节点,则该节点可以由该节点的后继节点进行替代。然后可以从后继节点的位置递归向下操作以删除后继节点。
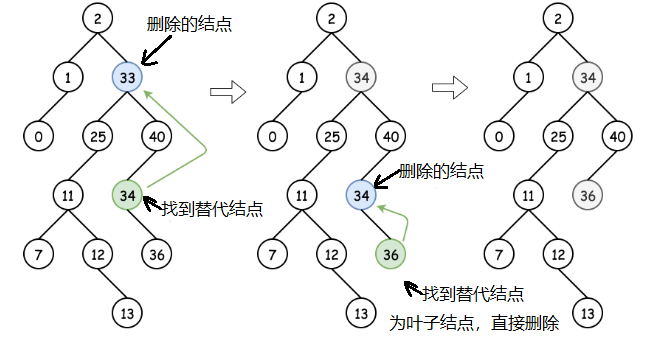
- 所删除的节点没有右节点但是有左节点。用它的前驱节点进行替代,然后再递归的向下删除前驱节点。

2.3.2 该题的伪代码
if(key > root.val)//说明要删除的节点在右子树
root等于rchild;
if(key < root.val)//说明要删除的节点在左子树
root等于lchild;
if(key == root.val)//则该节点就是我们要删除的节点
if(该节点是叶子节点)//直接删除
root = null;
else if(该节点有右节点)
root.val = successor.val;//用后继节点的值替代
删除后继节点;
else if(只有左节点)
root.val = predecessor.val;//它的前驱节点的值替代
删除前驱节点;
2.3.3 运行结果

2.3.4分析该题目解题优势及难点
优势:让我真正接触到了二叉树中数据的删除操作,算是增长了见识。
难点:对于被删除的结点,有多种情况,而每种情况删除的操作并不一样,以及如何找到对应替代结点也是难处。

