描述
二维平面上,给定 n 个点 {ai} 和 m 个点 {bi},且保证这 n+m 个点中任意两个点的 x 坐标和 y 坐标均不相同。
对于每个bi,判断是否存在由3个 ai, aj, ak (1 ≤ i, j, k ≤ n, i ≠ j ≠ k ) 点组成的三角形包含 bi(在三角形边上也算包含;允许三点共线的三角形,此时只有 bi 在三点中任意两点的线段上才算包含)。
输入
第一行为一个整数 n。接下来 n 行,其中第 i 行有两个整数,表示 ai 的横、纵坐标。
第一行为一个整数 m。接下来 m 行,其中第 i 行有两个整数,表示 bi 的横、纵坐标。
输出
输出 m 行,第 i 行为一个整数 0 或 1,分别表示是否存在一个三角形包含该 bi。
样例输入
3
1 -6
-10 -3
1 6
3
-2 7
-4 -3
-3 2
样例输出
0
1
1
限制
n, m ≥ 3;
其中30%的数据,n, m ≤ 200;
另外30%的数据,n, m ≤ 2000;
剩下40%的数据,n, m ≤ 300000。
时间:3 sec
空间:256 MB
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
思路
这是一道凸包应用的题目。凸包是一个点集所能围成的最大凸多边形区域。那么:
① 若点集 B 中的某点 b 能被点集 A 中的某三个点包围,那么它一定在点集 A 的凸包内(包括边界上)。
② 从点集 A 凸包上的某点开始,它所辐射的对角线(凸包上一点与凸包上其他点的连线)可以将凸包分成若干三角形区域。若 b 能被点集 A 中的某三个点包围,那么它一定在某两条对角线构成的三角形区域内。
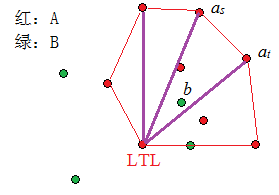
如下图所示,红色的点为点集 A,绿色的点为点集 B,红线围成的区域为 A 的凸包,LTL为我们选定的凸包上一点(它可以任意选择,一般选择 y 最小的点,若不唯一,再选择 x 最小的),它与凸包上其他点的连线将凸包分割成若干三角形部分。可以看到,B 中能被 A 包围的点一定在某个这些对角线构成的三角形内。
根据上面的分析,我们可以先求点集 A 的凸包(比如,卷包裹法、上下凸壳法等);然后从 A 凸包上某点开始(比如上图中的LTL点),找到 b 点最近的两条对角线,然后判断 b 能否被这两条对角线上三个 A 中的点包围。例如,对于上图中的 b 点,设法找到 at、as,然后判断 b 能否被 LTL、at、as围成的三角形包围。
如何快速找到离某点最近的两条对角线呢。我们可以使用二分查找。这就要对 A 凸包上的点排序,顺序就是其相对 LTL 的极角。比如上图中的 as 和 at 两点,从LTL看去,as 在 at 左侧,则 as > at 。注意,如果两个点与LTL位于同一直线上,则距离 LTL 更近的点更小。这样,就可以通过二分查找快速的找到 b 离最近的两条对角线了。
综上所述,可以将算法要旨总结如下图所示。注:① lower_bound 就是 C++ 标准模板库中的 lower_bound,返回有序序列中不小于我们查找对象的最小值。② 判断 b 是否在三角形内是利用三次 toLeft 判断实现的。

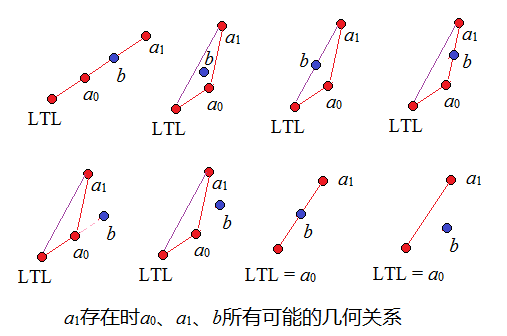
关于 toLeft(x, a, b):判断点 x 是否在向量 ab 的左侧。下图中所示的情况返回值均为 true。这样做是为了保证 b 在某条对角线上甚至与凸包上某点重合时都能正确判断(对于此题,数据保证无重合)。判断的方法是:先观察 ab 与 ax 的外积,若外积大于0则返回 true;若外积等于0,则再观察 ab 与 ax 的内积,内积大于等于0则返回 true。其他情况均返回 false。可以证明,对于如下图所示的所有可能的 LLT, a0, a1, b 的几何关系,应用三次上述 toLeft 测试都可以得到正确的判断。

复杂度:找到凸包 O(nlogn),二分查找 O(logn),三角形内部判断 O(1),故总的时间复杂度 O(mlog(n) + nlog(n)),n 为 A 点集中点个数,m 为 B 点集中点个数。
C++代码
这里为了方便,用了手头已有的上下凸壳法的模板求凸包。其实,用卷包裹法更方便,因为卷包裹法求凸包时就要先找LTL点,然后关于LTL点排序。
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 300005; // 存储二维平面点 struct ip { int x, y; ip(int x = 0, int y = 0) : x(x), y(y) { } void ri() { scanf("%d %d", &x, &y); } }; // iv表示一个向量类型,其存储方式和ip一样 typedef ip iv; // 先比较x轴再比较y轴 bool operator < (const ip &a, const ip &b) { return a.x == b.x ? a.y < b.y : a.x < b.x; } // 两点相减得到的向量 iv operator - (const ip &a, const ip &b) { return iv(a.x - b.x, a.y - b.y); } // 计算a和b的叉积(外积) ll operator ^ (const iv &a, const iv &b) { return (ll)a.x * b.y - (ll)a.y * b.x; } // 计算a和b的点积(内积) ll operator * (const iv &a, const iv &b) { return (ll)a.x * b.x + (ll) a.y * b.y; } class myComp { private: long long ltl_x, ltl_y; // 存储左下角点的坐标 public: myComp() : ltl_x(0), ltl_y(0) { } myComp(int x, int y){ ltl_x = (long long)x; ltl_y = (long long)y; } bool operator()(const ip & p1, const ip & p2) { long long x1 = (long long) p1.x - ltl_x, y1 = (long long) p1.y - ltl_y; long long x2 = (long long) p2.x - ltl_x, y2 = (long long) p2.y - ltl_y; long long outter_product = x1 * y2 - x2 * y1; if ( outter_product > 0 ) return true; else if ( outter_product == 0 ) // 若LTL、p1和p2共线 { long long x3 = (long long) p2.x - (long long) p1.x; long long y3 = (long long) p2.y - (long long) p1.y; if ( x3 * x1 + y3 * y1 > 0 ) // 若 LTL->p1 与 p1->p2 方向相同(用内积判断),则p1到LTL距离更短 return true; } return false; } }; /* 判断点 c 是否在 ab 向量的左侧。若 c 在 ab 上,或者 a→b 正向延长线上,或者 c 与 a 或 b 重合,返回皆为 true。 */ bool toLeft(ip & c, ip & a, ip & b) { long long x_ab = (long long) b.x - (long long) a.x; long long y_ab = (long long) b.y - (long long) a.y; long long x_ac = (long long) c.x - (long long) a.x; long long y_ac = (long long) c.y - (long long) a.y; long long outter_product = x_ab * y_ac - x_ac * y_ab; long long inner_product = x_ab * x_ac + y_ab * y_ac; if ( outter_product > 0 || (outter_product == 0 && inner_product >= 0) ) return true; return false; } /* 计算二维点数组a的凸包,将凸包放入b数组中,下标均从0开始 a, b:如上 n:表示a中元素个数 返回:凸包元素个数 */ int convex(ip * a, ip * b, int n) { // 升序排序 sort(a, a+n); // n = unique(a, a+n) - a; // 若题目中有重复点,必须去重 int m = 0; // 求下凸壳 for ( int i = 0; i < n; ++i ) { for ( ; m > 1 && ((b[m-1] - b[m-2]) ^ (a[i] - b[m-2])) < 0; --m ); b[m++] = a[i]; } // 求上凸壳 for ( int i = n - 2, t = m; i >= 0; --i ) { for ( ; m > t && ((b[m-1] - b[m-2]) ^ (a[i] - b[m-2])) < 0; --m ); b[m++] = a[i]; } return m - 1; } /* 对第n_b个点构成的点集B(坐标从b开始存储)中每个点,判断是否能被n_a个点构成的点集A(坐标从a开始存储)中的三个点包围。 */ vector<int> isSurrounded(ip * a, ip * b, int n_a, int n_b); ip A[N], B[N]; int main() { int n = 0, m = 0; // 点集A中点的数量n和点集B中点的数量m // 读入各点坐标 scanf("%d", &n); for ( int i = 0; i < n; ++i ) A[i].ri(); scanf("%d", &m); for ( int i = 0; i < m; ++i ) B[i].ri(); // 求解 vector<int> ans = isSurrounded(A, B, n, m); // 打印结果 for ( int i = 0; i < m; ++i ) printf("%d\n", ans[i]); return 0; } vector<int> isSurrounded(ip * a, ip * b, int n_a, int n_b) { vector<int> ans; ans.resize(n_b); // 求a的凸包 (如果不找到凸包,直接在整个点集A上执行下面的判断是不正确的) ip * conv = new ip[n_a]; int n_conv = convex(a, conv, n_a); // 找到A中的LTL,并将它换到conv指向的位置 (即conv数组的第0个元素) ip ltl(conv->x, conv->y); ip * p = conv; for ( int i = 1; i < n_conv; ++i ) { if ( (conv+i)->y < ltl.y || ((conv+i)->y == ltl.y && (conv+i)->x < ltl.x ) ) { ltl.x = (conv+i)->x; ltl.y = (conv+i)->y; p = conv+i; } } p->x = conv->x; p->y = conv->y; conv->x = ltl.x; conv->y = ltl.y; // 对conv中各点关于LTL进行极角排序 sort(conv+1, conv+n_conv, myComp(ltl.x, ltl.y)); // 对B中各点判断其是否能被A中的三个点包围 for ( int i = 0; i < n_b; ++i ) { if ( b[i].y < ltl.y || (b[i].y == ltl.y && b[i].x < ltl.x ) ) { ans[i] = 0; continue; } // 找到A凸包中不小于b[i]的最小点a1 ip * a1 = lower_bound(conv+1, conv+n_conv, b[i], myComp(ltl.x, ltl.y)); ip * a0 = a1 - 1; if ( (a1 - a) == n_conv ) // 若找不到这样的a1,则不能被包围 ans[i] = 0; else { if ( toLeft(b[i], ltl, *a0) && toLeft(b[i], *a0, *a1) && toLeft(b[i], *a1, ltl) ) ans[i] = 1; else ans[i] = 0; } } return ans; }


