最小生成树的概念:
对于一张无向带权连通图,若它的一张子图满足:① 连通性,即图中所有顶点相互连通;② 该子图所有边的权值之和最小。它必定是一棵树(无环路),则该子图称为原图的一棵最小生成树。类似的,也可以定义最大生成树。
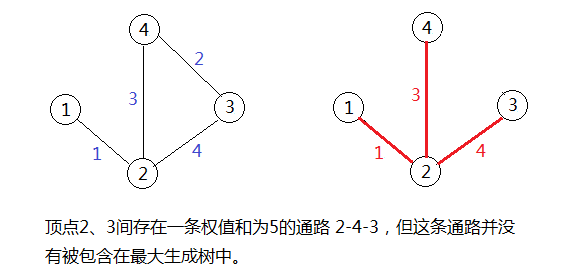
注意,最大生成树中,任意两点间通路的长度并不一定是原图中该两点通路中权值和最大的那条。如下图所示例子。
求最小生成树的Kurskal算法:
初始每个顶点 v1, v2, ..., vn 各自构成一棵只含它自身的树,这些点构成一个森林。由于此时各树只含一个顶点,它是一棵最小生成树。
循环,对于当前未被选择的所有边:
选出权值最小的边 e<vi, vj>
如果该边 e 连接的两个顶点 vi 和 vj 当前分别处在不同的两棵树中,这两棵树分别记为 T(vi), T(vj),则:e<vi, vj> 一定包含在最小生成树中,记录;且将 T(vi) 和 T(vj) 合并为一棵树。
如果该边 e 连接的两个顶点 vi 和 vj 当前处在同一棵树中,则丢弃改边。
循环直至森林只剩1颗树(已选择了 n-1 条边),这棵树就是最小生成树。
技巧:
可以使用并查集来维护森林里各树包含的顶点,初始每个顶点各自构成一个集合,树的合并就是将一个集合合并到另一个集合中。
可以使用堆(优先队列)来维护各边,每次从堆顶取出权值最小的边。
复杂度:
设原图中顶点个数为|V|,边数目为|E|,复杂度 ~ O(|E|log|V|)。
当为稀疏图时(|E|与|V|同量级),复杂度优于Prim算法。


