排序算法

一、冒泡排序

时间复杂度：最好一轮刚好完成，则为O(n) ；最坏两层循环全执行完才完成，则为 O(n2)；

空间复杂度：O(1)

稳定性：稳定【只有大于才交换，否则不交换，所以在前后有相同时保持了原数组顺序】

　　　 // 内层循环：跑一轮，把最大的放最后；然后外层循环重复跑
      // 每一轮结束最后面的都是最大的
      function BubbleSortMe(arr) {
        for (let x = 0; x < arr.length-1; x++) {
          // 外层循环次数arr.length-1; 内层因为没轮过后最后面都会确定一个最大数，所以内层循环次数就是 arr.length-1-x 减去轮数即可；
          for (let y = 0; y < arr.length-1-x; y++) {
            if(arr[y]>arr[y+1]){
              [arr[y], arr[y+1]] = [arr[y+1], arr[y]]
            }
            // 每轮执行次数
            console.log(x)
          }
        }
        return arr
      }
      var arr=[10,7,9,11,22,33,4444444,2,0,1000];
      BubbleSortMe(arr);
      console.log(arr);

二、选择排序

时间复杂度：都需要两层循环全执行完才完成，则为 O(n2)；

空间复杂度：O(1)

稳定性：不稳定【内层每次寻找的最小的数都是一轮循环完后找到的数，所以在前后有相同时后面的数最终会排到前面去】

　　 function selectionSort(arr) {
      var minIndex;
      for (var i = 0; i < arr.length; i++) {
          minIndex = i;
          for (var j = i + 1; j < arr.length; j++) {
              if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                  minIndex = j;                 // 将最小数的索引保存
              }
          }
　　　　　　console.log(i)外层循环此时的数与内层寻找的最小数交换
          [arr[minIndex], arr[i]] = [arr[i], arr[minIndex]]
      }
      return arr;
    }
    var array = [1,3,5,4,2,7,9,32,331,32,32331,313,89,21];
    console.log(selectionSort(array))

三、插入排序

时间复杂度：最好一轮刚好完成，则为O(n) ；最坏两层循环全执行完才完成，则为 O(n2)；

空间复杂度：O(1)

稳定性：稳定【对于未排序数据，在已排序序列中从后向前扫描，找到比自己大的相应位置前并插入，所以在前后有相同时后面的数不动】

　　 function insertionSort(arr) {
      for (var i = 1; i < arr.length; i++) {
        var preIndex = i - 1; //默认已排序的元素 第一个
        var temp = arr[i] //需要排位的元素 先额外缓存起来
        // 套用内循环，使得需要调整的元素赋值给它后面的一个位置上，形成依次挪位，最后因为内循环在判断条件不生效的时候停止意味着找到了需要排位的元素的正确位置，然后赋值上去，完成排序
        while(preIndex >= 0 && arr[preIndex] > temp) { //在已排序好的队列中从后向前扫描
          arr[preIndex+1] = arr[preIndex]; //已排序的元素大于新元素，将该元素移到后面一个位置，即大数往后走  此处修改了arr[i]值，所以需要一个temp，而不是直接使用arr[i]
          preIndex--; // 最终大数走到合适位置停止，此时preIndex也变成合适位置
        }
        arr[preIndex+1] = temp; // 此时合适位置的preIndex赋值为需排位的数
      }
      return arr;
    }
    var array = [3,2,1,5,4,22,7,9,32,331,32,32331,313,89,21];
    insertionSort(array)
    console.log(array)

四、希尔排序：【以间隔分组后，相同间隔的数执行插排，然后间隔递减，执行相同操作，则会越来越基本有序，直到成功】

时间复杂度：最好一轮刚好完成，则为O(n) ；最坏两层循环全执行完才完成，则为 O(n2)；

空间复杂度：O(1)

稳定性：不稳定【在插入排序的基础上，优先比较相同间隔的元素，所以在前后有相同时可能会有变化】

比普通插入排序快的原因：间隔大的时候如果需要往前挪，则挪的次数小（因为间隔大往前跳的快）；间隔小的时候如果需要往前挪，挪的距离小（因为随着间隔越来越小，基本越有序，所以距离合适位置距离小，挪的次数也就小）

　　function shellSort(arr) {
        // 外层循环主要为了减少不长，减少步长到最终为1
        for(var gap = Math.floor(arr.length / 3); gap > 0; gap = Math.floor(gap / 3)) {
            // 内层循环使用的插入排序与普通的插入排序基本一致，只是每次移动的步长变为 gap 而不是 1：即while内根据gap跳着比较然后交换
            for(var i = gap; i < arr.length; i++) {
                while(i - gap >= 0 && arr[i - gap] > arr[i]) {
                    [arr[i], arr[i - gap]] = [arr[i - gap], arr[i]]
                    i = i - gap; // 最终大数走到合适位置停止，此时preIndex也变成合适位置
                }
            }
        }
        return arr;
    }
    var array = [1,3,5,4,2,7,9,32,331,32,32331,313,89,21];
    shellSort(array)
    console.log(array)

五、归并排序：【分治法】

时间复杂度：两层循环全执行完才完成，则为 O(nLog2N)；

空间复杂度：O(N)

稳定性：稳定【因为拆分是左右拆，合并是左右合并，所以在前后有相同时不会有变化】

　　 // 先递归的分解数列，再合并数列
    // 将一个数组拆成A、B两个小组，两个小组继续拆，直到每个小组只有一个元素为止。
    // 按照拆分过程逐步合并小组，由于各小组初始只有一个元素，可以看做小组内部是有序的，合并小组可以被看做是合并两个有序数组的过程。
    // 对左右两个小数列重复第二步，直至各区间只有1个数。
    function mergeSort(arr) {
        console.log(arr)
        var len = arr.length;
        if(len < 2) {
            return arr;
        }
        var middle = Math.floor(len / 2),
            left = arr.slice(0, middle),
            right = arr.slice(middle);
        // 挂起mergeSort(left)，一直left拆完，然后把left合并完，才执行right
        return merge(mergeSort(left), mergeSort(right));
    }
    function merge(left, right)
    {
        var result = [];
        console.log(left)
        console.log(right)
        while (left.length && right.length) {
            if (left[0] <= right[0]) {
                result.push(left.shift());
            } else {
                result.push(right.shift());
            }
        }
        while (left.length)
            result.push(left.shift());
        while (right.length)
            result.push(right.shift());
        console.log("将数组",left,'和',right,'合并为',result)
        debugger
        return result;
    }
    var array = [8,3,5,4,2,7,9,32,331,32,32331,313,89,21];
    mergeSort(array)
    console.log(mergeSort(array))

 

 

 

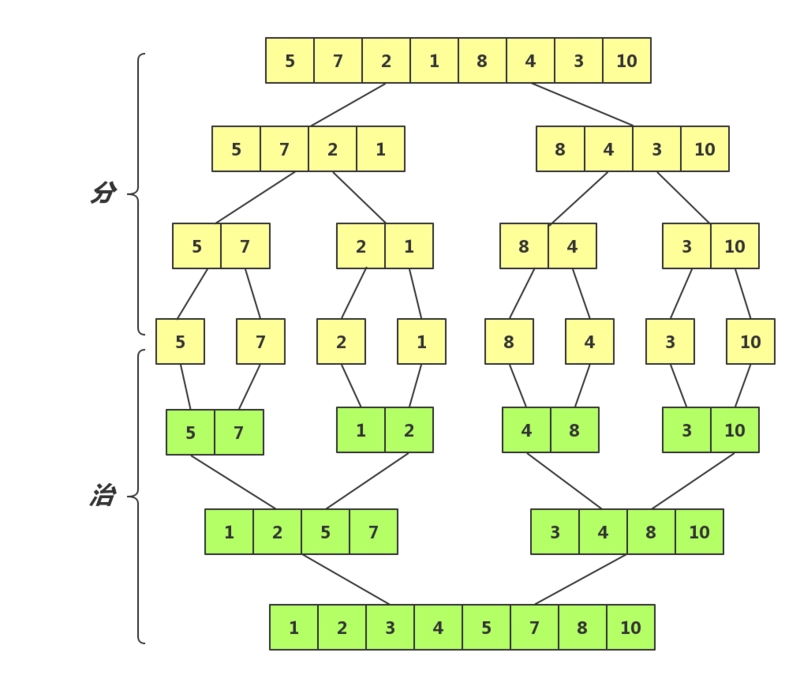
🌰：移动数组

function moveElement(arr, n) {
  if(Math.abs(n)>arr.length) n = n%arr.length
  return arr.slice(-n).concat(arr.slice(0,-n))
}

类似：moveElement([1,2,3,4,5],3)

返回：[3, 4, 5, 1, 2]

🌰：>> << >>>左移右移操作符

// length >> 1 和 Math.floor(arr.length / 2) 等价

涉及2进制操作：

xnum>>n    等价于   xnum除以2^n

xnum<<n    等价于   xnum乘以2^n

原理：十进制的情况下，比如100，右边少了一个0，不就是除以10了，那二进制也同理