数据结构之二叉树的构建C++版

二叉树的构建要注意与链式表的区别，二叉树这里的构建十分低级，每个树只是构建了一个单一的二叉树节点，总体来看是有下向上构建的。用户需要手动去构建自己需要的树，而不是直接去插入数据就到二叉树中了，因为不是链式结构的单一，二叉树十分丰富的。

提一下遍历：

迭代的方式遍历十分简单。先序、中序、后序遍历都只是针对根节点。比如中序，就是先遍历左子树-->根节点-->右子树。（根节点在中间）

/*
1) 树的基本概念:
    度：说白了就是节点拥有的子分支数
    叶子节点：说白了就是度为0的节点
    双亲:说白了就是父亲节点
    层次：约定根节点为1，以后的子节点依次递增
    高度：说白了就是层次最大的数
2）二叉树的类型
    1>满二叉树:叶子必须位于最后一层，并且其他节点度为2
    2>扩充二叉树：除叶子节点外,其他节点度为2
        1，扩充二叉树的最大特点在于他的外路径长度=内路径的长度+2*非叶节点的数目
        2，典型应用就是哈弗曼编码
    3>完全二叉树: 只有最后两层的节点的度能小于2，并且最后1层的叶子节点必须靠左边。
        1，将整个完全二叉树依照从左到右，从上到下的进行0-->n进行编号，若子节点序号为i,则父节点为(i-1)/2。
        2，典型的应用大小堆的实现。
    4>其他类型二叉树
3）森林与二叉树的互转
*/

template <class T>
struct  BTNode
{
    BTNode<T> *_lChild, *_rChild;
    T element;
    BTNode(const T &e) {
        element = e;
        _lChild = _rChild = NULL;
    }
};
template <class T>
class JBBinaryTree
{    
public:    
    JBBinaryTree();
    ~JBBinaryTree();
    BTNode<T> *_root;
    //清空当前树
    void clear();
    //获取到当前元素
    T getElement()    const;
    //判断当前二叉树是不是空二叉树
    bool isEmpty()    const;
    //构建一棵数
    void makeTree(const T &x,JBBinaryTree<T> *left,JBBinaryTree<T> *right);
    //拆除一棵数
    void breakTree(T &x,JBBinaryTree*left,JBBinaryTree*right);
    //前序遍历 统一采用递归遍历
    void preOrder(BTNode<T> *t);
    //中序遍历
    void inOrder(BTNode<T> *t);
    //后序遍历
    void postOrder(BTNode<T> *t);
};

template <class T>
JBBinaryTree<T>::JBBinaryTree()
{
    _root = NULL;
}

template<class T>
JBBinaryTree<T>::~JBBinaryTree()
{
    clear();
}

template<class T>
void JBBinaryTree<T>::clear() {
　　if(_root==NULL){
　　　　return;
　　}    
　　delete _root;
    _root = NULL;
}
template<class T>
T JBBinaryTree<T>::getElement() const {
    if (isEmpty()) {
        reurn NULL;
    }
    return _root->element;
}
template<class T>
bool JBBinaryTree<T>::isEmpty() const {
    return _root == NULL;
}
template<class T>
void JBBinaryTree<T>::makeTree(const T &x, JBBinaryTree<T> *left, JBBinaryTree<T> *right) {
    if (_root)return;//如果根节点不为空 就直接return 这实际上让用户操作起来十分不方便 不能自己构建自己 必须重一个节点
    _root = new BTNode<T>(x);//实例化二叉树根节点
    _root->_lChild = left->_root;//让左指针指向左子树的根节点
    _root->_rChild = right->_root;//让右指针指向右子树的根节点
    left->_root = right->_root = NULL;
}
template<class T>
void JBBinaryTree<T>::breakTree(T &x, JBBinaryTree*left, JBBinaryTree*right) {
    if (!_root || left == right || left->_root || right->_root) {
        //若此树本身就是空的，或则用于承接的左右树本身一样，或则用于承接的左子树不为空都直接退出
        return;
    }
    x = _root->element;//将这个树的根节点的元素域转移走
    left->_root = _root->_lChild;//将左子树单独拆成一棵树
    right->_root = _root->_rChild;//将右子树单独拆成一棵树
    clear();
}
template<class T>
void JBBinaryTree<T>::preOrder(BTNode<T> *t) {
    if (t) {
        printf("%d",t->element);
        preOrder(t->_lChild);
        preOrder(t->_rChild);
    }
}
template<class T>
void JBBinaryTree<T>::inOrder(BTNode<T> *t) {
    if (t) {
        inOrder(t->_lChild);
        printf("%d",t->element);
        inOrder(t->_rChild);
    }
}
template<class T>
void JBBinaryTree<T>::postOrder(BTNode<T> *t) {
    if (t) {
        postOrder(t->_lChild);
        postOrder(t->_rChild);
        printf("%d",t->element);
    }
}

下面看一下主程序

　　

#include "stdafx.h"
#include"stdlib.h"
#include"JBQueue.h"
#include"JBStack.h"
#include"JBBinaryTree.h"

int main()
{
    {
        JBBinaryTree<int> L,R,a,b,c,d,e;
        a.makeTree(0,&L,&R);
        b.makeTree(1,&L,&R);
        c.makeTree(2,&a,&b);
        d.makeTree(3,&a,&b);
        e.makeTree(4,&c,&d);
        printf("前序遍历：");
        e.preOrder(e._root);
        printf("\n中序遍历：");
        e.inOrder(e._root);
        printf("\n后序遍历：");
        e.postOrder(e._root);
        printf("\n");
    }
    system("pause");
    return 0;
}

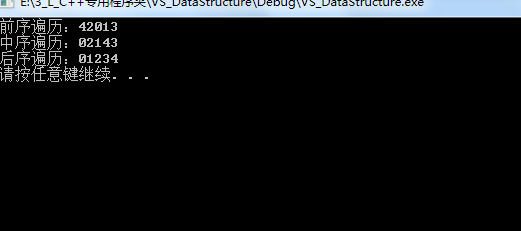
结果：