使用机器学习对曲线进行线性回归

简介

线性回归：根据数据，确定两种或两种以上变量间相互依赖的定量关系

评价曲线的拟合效果使用均方误差和R方值进行拟合质量评估

\[M S E=\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}^{\prime}-y_{i}\right)^{2} \]

R方值 \(\left(R^{2}\right)\) :

\[R^{2}=1-\frac{\sum_{i=1}^{m}\left(y_{i}^{\prime}-y_{i}\right)^{2}}{\sum_{i=1}^{m}\left(y_{i}-\overline{y_{i}}\right)^{2}}=1-\frac{M S E}{\text { 方差 }} \]

MSE越接近0越好R方值越接近1越好。

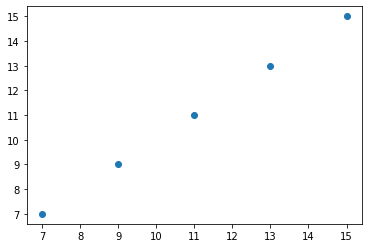
对于离散数据点。

x	y
1	7
2	9
3	11
4	13
5	15

进行机器学习线性回归操作

code

import pandas as pd
data = pd.read_csv('generated_data.csv')
data.head()
x = data.loc[:,'x']
y = data.loc[:,'y']
print(x,y)
from matplotlib import pyplot as plt
plt.figure(figsize=(10,10))
plt.scatter(x,y)
plt.show()
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
import numpy as np
x = np.array(x)
x = x.reshape(-1,1)
y = np.array(y)
y = y.reshape(-1,1)
print(x,y)
lr_model.fit(x,y)
y_predict = lr_model.predict(x)
print(y_predict)
y_3 = lr_model.predict([[3.5]])
print(y_3)
from sklearn.metrics import mean_squared_error,r2_score
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE,R2)
plt.figure()
plt.scatter(y,y_predict)
plt.show()

image