简介
其实流体力学就是专有名词多, 比如流固耦合. 其实就是流体对固体的一个作用. 固体对流体的一个作用而已. 搞得神神秘秘的服了.
使用诺依曼边界条件的建议水滴代码
using UnityEngine;
using System.Collections;
public class wave_motion : MonoBehaviour
{
int size = 100;
float rate = 0.005f; // like alpha ?
float gamma = 0.004f;
float damping = 0.996f;
float[,] old_h;
float[,] low_h; // ei
float[,] vh;
float[,] b;
bool [,] cg_mask;
float[,] cg_p;
float[,] cg_r;
float[,] cg_Ap;
bool tag=true;
Vector3 cube_v = Vector3.zero;
Vector3 cube_w = Vector3.zero;
int[,] dirs;
// Use this for initialization
void Start ()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
mesh.Clear ();
Vector3[] X=new Vector3[size*size];
for (int i=0; i<size; i++)
for (int j=0; j<size; j++)
{
X[i*size+j].x=i*0.1f-size*0.05f;
X[i*size+j].y=0.3f;
X[i*size+j].z=j*0.1f-size*0.05f;
}
int[] T = new int[(size - 1) * (size - 1) * 6];
int index = 0;
for (int i=0; i<size-1; i++)
for (int j=0; j<size-1; j++)
{
T[index*6+0]=(i+0)*size+(j+0);
T[index*6+1]=(i+0)*size+(j+1);
T[index*6+2]=(i+1)*size+(j+1);
T[index*6+3]=(i+0)*size+(j+0);
T[index*6+4]=(i+1)*size+(j+1);
T[index*6+5]=(i+1)*size+(j+0);
index++;
}
mesh.vertices = X;
mesh.triangles = T;
mesh.RecalculateNormals ();
low_h = new float[size,size];
old_h = new float[size,size];
vh = new float[size,size];
b = new float[size,size];
cg_mask = new bool [size,size];
cg_p = new float[size,size];
cg_r = new float[size,size];
cg_Ap = new float[size,size];
//方向
dirs = new int[4, 2];
dirs[0, 0] = 1;
dirs[0, 1] = 0;
dirs[1, 0] = -1;
dirs[1, 1] = 0;
dirs[2, 0] = 0;
dirs[2, 1] = 1;
dirs[3, 0] = 0;
dirs[3, 1] = -1;
for (int i=0; i<size; i++)
for (int j=0; j<size; j++)
{
low_h[i,j]=99999;
old_h[i,j]= 0.3f;
vh[i,j]=0;
}
}
void A_Times(bool[,] mask, float[,] x, float[,] Ax, int li, int ui, int lj, int uj)
{
for(int i=li; i<=ui; i++)
for(int j=lj; j<=uj; j++)
if(i>=0 && j>=0 && i<size && j<size && mask[i,j])
{
Ax[i,j]=0;
if(i!=0) Ax[i,j]-=x[i-1,j]-x[i,j];
if(i!=size-1) Ax[i,j]-=x[i+1,j]-x[i,j];
if(j!=0) Ax[i,j]-=x[i,j-1]-x[i,j];
if(j!=size-1) Ax[i,j]-=x[i,j+1]-x[i,j];
}
}
float Dot(bool[,] mask, float[,] x, float[,] y, int li, int ui, int lj, int uj)
{
float ret=0;
for(int i=li; i<=ui; i++)
for(int j=lj; j<=uj; j++)
if(i>=0 && j>=0 && i<size && j<size && mask[i,j])
{
ret+=x[i,j]*y[i,j];
}
return ret;
}
void Conjugate_Gradient(bool[,] mask, float[,] b, float[,] x, int li, int ui, int lj, int uj)
{
//Solve the Laplacian problem by CG.
A_Times(mask, x, cg_r, li, ui, lj, uj);
for(int i=li; i<=ui; i++)
for(int j=lj; j<=uj; j++)
if(i>=0 && j>=0 && i<size && j<size && mask[i,j])
{
cg_p[i,j]=cg_r[i,j]=b[i,j]-cg_r[i,j];
}
float rk_norm=Dot(mask, cg_r, cg_r, li, ui, lj, uj);
for(int k=0; k<128; k++)
{
if(rk_norm<1e-10f) break;
A_Times(mask, cg_p, cg_Ap, li, ui, lj, uj);
float alpha=rk_norm/Dot(mask, cg_p, cg_Ap, li, ui, lj, uj);
for(int i=li; i<=ui; i++)
for(int j=lj; j<=uj; j++)
if(i>=0 && j>=0 && i<size && j<size && mask[i,j])
{
x[i,j] +=alpha*cg_p[i,j];
cg_r[i,j]-=alpha*cg_Ap[i,j];
}
float _rk_norm=Dot(mask, cg_r, cg_r, li, ui, lj, uj);
float beta=_rk_norm/rk_norm;
rk_norm=_rk_norm;
for(int i=li; i<=ui; i++)
for(int j=lj; j<=uj; j++)
if(i>=0 && j>=0 && i<size && j<size && mask[i,j])
{
cg_p[i,j]=cg_r[i,j]+beta*cg_p[i,j];
}
}
}
void get_vh(float[,] new_h, int blk_id)
{
Vector3 p = new Vector3(0, 0, 0);
if (blk_id == 1)
{
GameObject block = GameObject.Find("Cube");
p = block.transform.position;
}
else if(blk_id == 2)
{
GameObject block = GameObject.Find("Block");
p = block.transform.position;
}
Mesh mesh = GetComponent<MeshFilter>().mesh;
Vector3[] X = mesh.vertices;
int li = (int)Mathf.Ceil((p.x - 0.5f + 5f) / 0.1f);
int lj = (int)Mathf.Ceil((p.z - 0.5f + 5f) / 0.1f);
int ui = (int)Mathf.Floor((p.x + 0.5f + 5f) / 0.1f);
int uj = (int)Mathf.Floor((p.z + 0.5f + 5f) / 0.1f);
// for block 1, calculate low_h;
for (int i = li; i <= ui; i++)
for (int j = lj; j <= uj; j++)
if(i >= 0 && j >= 0 && i < size && j < size)
{
cg_mask[i, j] = true;
low_h[i, j] = 0f;
}
else
{
cg_mask[i, j] = false;
low_h[i, j] = new_h[i, j];
}
// then set up b and cg_mask for conjugate gradient.
for(int i=0; i<size; i++)
{
for(int j=0; j<size; j++)
{
b[i, j] = (new_h[i, j] - low_h[i, j]) / rate;
}
}
//Solve the Poisson equation to obtain vh (virtual height).
Conjugate_Gradient(cg_mask, b, vh, li, ui, lj, uj);
}
void Shallow_Wave(float[,] old_h, float[,] h, float [,] new_h)
{
//Step 1:
//TODO: Compute new_h based on the shallow wave model.
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
float hi_1j = i > 0 ? h[i - 1, j] : h[i, j];
float hi1j = i + 1 < size ? h[i + 1, j] : h[i, j];
float hij_1 = j > 0 ? h[i, j - 1] : h[i, j];
float hij1 = j + 1 < size ? h[i, j + 1] : h[i, j];
new_h[i, j] = h[i, j] + (h[i, j] - old_h[i, j]) * damping +
rate * (hi1j + hij1 + hi_1j + hij_1 - 4 * h[i, j]);
}
}
//Step 2: Block->Water coupling
//for (int i = 0; i < size; i++)
//{
// for (int j = 0; j < size; j++)
// {
// vh[i, j] = 0;
// }
//}
//TODO: for block 1, calculate low_h.
//TODO: then set up b and cg_mask for conjugate gradient.
//TODO: Solve the Poisson equation to obtain vh (virtual height).
//get_vh(new_h, 1);
//TODO: for block 2, calculate low_h.
//TODO: then set up b and cg_mask for conjugate gradient.
//TODO: Solve the Poisson equation to obtain vh (virtual height).
//get_vh(new_h, 2);
//TODO: Diminish vh.
//TODO: Update new_h by vh.
//for (int i = 0; i < size; i++)
// for (int j = 0; j < size; j++)
// if (i >= 0 && j >= 0 && i < size && j < size)
// {
// if (i != 0) new_h[i, j] += (vh[i - 1, j] - vh[i, j]) * rate;
// if (i != size - 1) new_h[i, j] += (vh[i + 1, j] - vh[i, j]) * rate;
// if (j != 0) new_h[i, j] += (vh[i, j - 1] - vh[i, j]) * rate;
// if (j != size - 1) new_h[i, j] += (vh[i, j + 1] - vh[i, j]) * rate;
// }
//Step 3
//TODO: old_h <- h; h <- new_h;
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
old_h[i, j] = h[i, j];
h[i, j] = new_h[i, j];
}
}
//Step 4: Water->Block coupling.
//More TODO here.
}
// Update is called once per frame
void Update ()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
Vector3[] X = mesh.vertices;
float[,] new_h = new float[size, size];
float[,] h = new float[size, size];
//TODO: Load X.y into h.
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
h[i, j] = X[i * size + j].y;
}
}
if (Input.GetKeyDown ("r"))
{
//TODO: Add random water.
int i = Random.Range(0, size);
int j = Random.Range(0, size);
float rt = Random.value;
float r = 0;
for (int k = 0; k < 4; k++)
{
int ni = i + dirs[k, 0];
int nj = j + dirs[k, 1];
if (ni >= 0 && ni < size && nj >= 0 && nj < size)
{
r += h[ni, nj] * rt;
h[ni, nj] -= h[ni, nj] * rt;
}
}
//Debug.Log("add_r:" + r);
h[i, j] += r;
}
for(int l=0; l<8; l++)
{
Shallow_Wave(old_h, h, new_h);
}
//TODO: Store h back into X.y and recalculate normal.
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
X[i * size + j].y = h[i, j];
}
}
mesh.vertices = X;
mesh.RecalculateNormals();
}
}
波动效果的公式
波动公式

经过转换其中的变量

这里简化ei=0 即 cube 块 直接和底面进行接触, 如果只考虑一个固体->流体的情况
vh 表示 虚拟高度
接下来就使用这张image
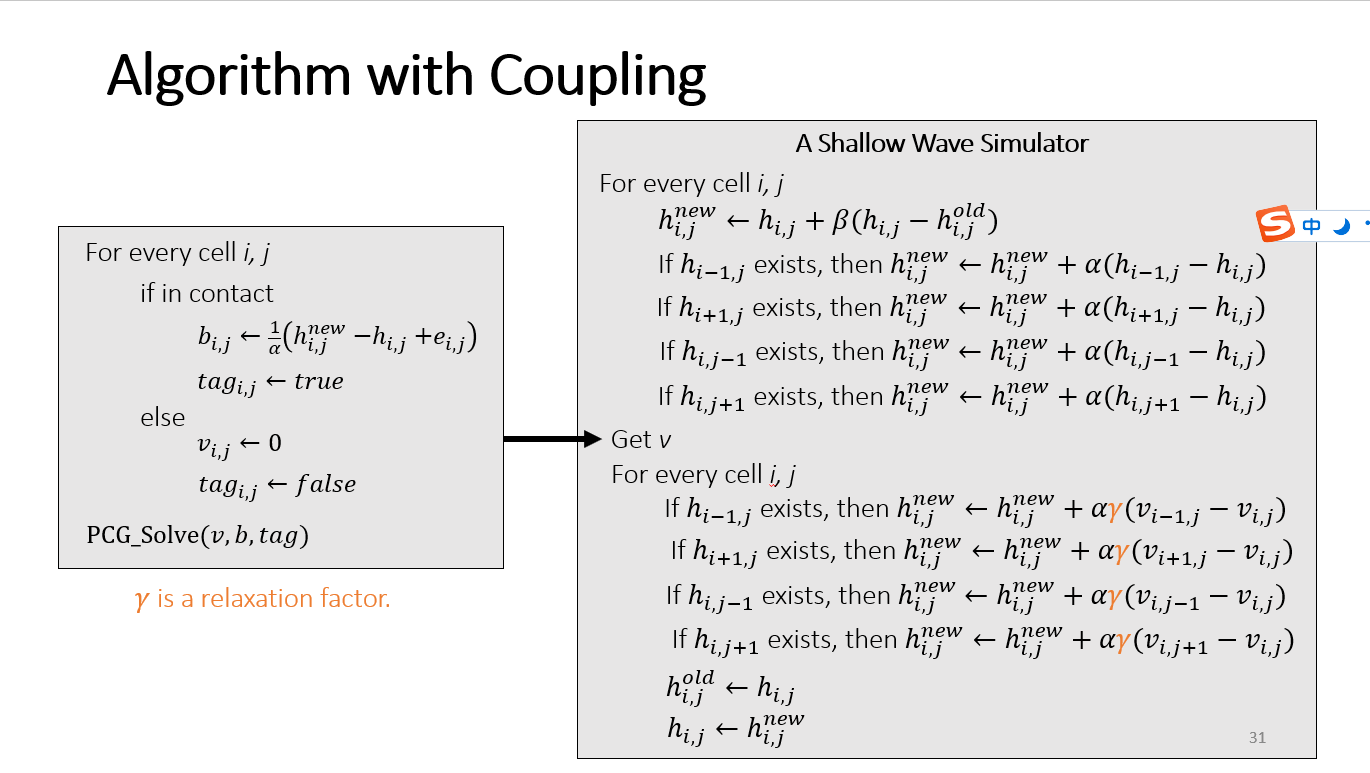
上面的图其实类似

只不过一个是真实高度一个是虚拟高度引起的江河湖海的高度变化.
---------------------------我的天空里没有太阳,总是黑夜,但并不暗,因为有东西代替了太阳。虽然没有太阳那么明亮,但对我来说已经足够。凭借着这份光,我便能把黑夜当成白天。我从来就没有太阳,所以不怕失去。
--------《白夜行》





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本