简介
PDB 比 隐式积分法 速度快很多.
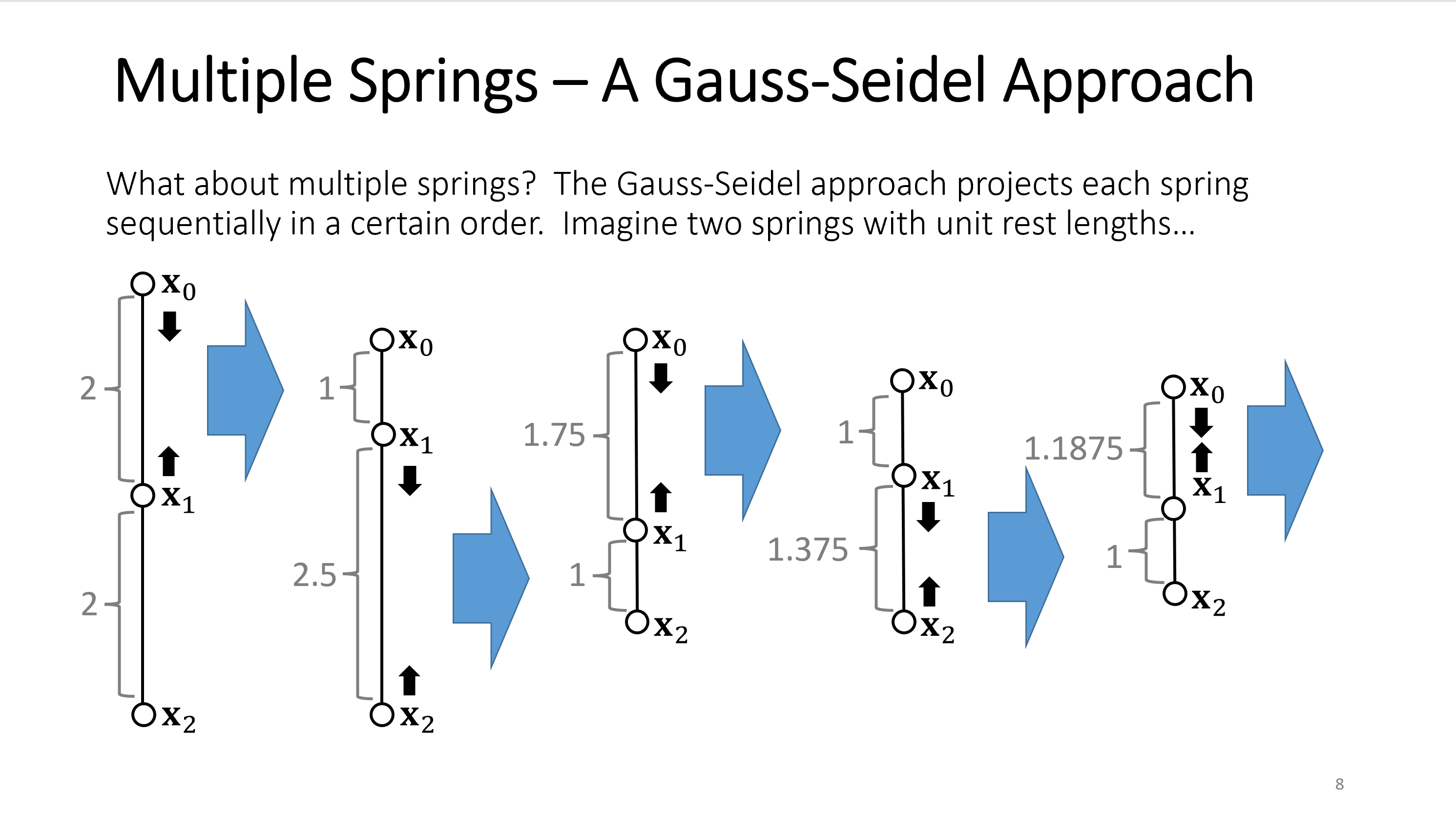
全称 Position Based Dynamics 粒子动力学系统, 什么是PBD呢? 个人的理解就是, 多次迭代, 达到一步的稳定状态. 然后更新整个系统的状态. 简单的说, 就是对于局部的模拟扩展到全局. 经过一定的迭代, 达到稳态.
可以参看Image中的第一幅图片. 对于单个系统的更新, 导致的全局的收敛. 但是必须达到多次迭代, 才能达到类似整体的一次迭代.
参考文献
师弟代码~~
Q&A
Q1
In the Update function, set up the PBD solver as a particle system. Specifically, for every vertex, damp the velocity (as in 1.a), update the velocity by gravity, and finally
update the position:
\[\mathbf{x}_{i} \leftarrow \mathbf{x}_{i}+\Delta t \mathbf{v}_{i}
\]
简单而言就是, 改变速度. 通过重力改变, 然后加上速度衰减, 然后根据速度的改变更新坐标.
V[i] += g * t;
V[i] *= damping;
X[i] += t * V[i];
Q2
1.b. Strain limiting (4 Points) In the Strain Limiting function, implement position-based
dynamics in a Jacobi fashion. The basic idea is to define two temporary arrays sum x[] and sum n[]
to store the sums of vertex position updates and vertex count updates. At the beginning of the
function, set both arrays to zeros. After that, for every edge e connecting i and j, update the arrays:
\[\begin{array}{ll}
\operatorname{sum}_{\mathbf{}} \mathbf{x}_{i} \leftarrow \operatorname{sum}_{-} \mathbf{x}_{i}+\frac{1}{2}\left(\mathbf{x}_{i}+\mathbf{x}_{j}+L_{e} \frac{\mathbf{x}_{i}-\mathbf{x}_{j}}{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|}\right), & \text { sum_n }_{i} \leftarrow \text { sum_n }_{i}+1, \\
\text { sum_ } \mathbf{x}_{j} \leftarrow \text { sum_ } \mathbf{x}_{j}+\frac{1}{2}\left(\mathbf{x}_{i}+\mathbf{x}_{j}-L_{e} \frac{\mathbf{x}_{i}-\mathbf{x}_{j}}{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|} \|,\right. & \text { sum_n }_{j} \leftarrow \text { sum_ } n_{j}+1 .
\end{array}
\]
Finally, update each vertex as:
\[\mathbf{v}_{i} \leftarrow \mathbf{v}_{i}+\frac{1}{\Delta t}\left(\frac{0.2 \mathbf{x}_{i}+s u m_{-} \mathbf{x}_{i}}{0.2+s u m_{-} n_{i}}-\mathbf{x}_{i}\right), \quad \mathbf{x}_{i} \leftarrow \frac{0.2 \mathbf{x}_{i}+s u m_{-} \mathbf{x}_{i}}{0.2+\operatorname{sum_n} n_{i}}
\]
作者给出的 \(\alpha = 0.2f\) 可以参考最后一张图.
void Strain_Limiting()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
Vector3[] vertices = mesh.vertices;
//Apply PBD here.
Vector3[] sum_x = new Vector3[vertices.Length];
int[] num_x = new int[vertices.Length];
for(int i=0; i<vertices.Length; i++)
{
sum_x[i] = new Vector3(0, 0, 0);
num_x[i] = 0;
}
for(int ei = 0; ei < L.Length; ei++)
{
int i = E[ei * 2];
int j = E[ei * 2 + 1];
Vector3 xi_xj = vertices[i] - vertices[j];
float len_ij = L[ei] / xi_xj.magnitude;
sum_x[i] += (vertices[i] + vertices[j] + len_ij * (xi_xj)) / 2;
sum_x[j] += (vertices[i] + vertices[j] - len_ij * (xi_xj)) / 2;
num_x[i]++;
num_x[j]++;
}
for(int i=0; i<vertices.Length; i++)
{
if (i == 0 || i == 20) continue;
V[i] += ((0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f) -
vertices[i]) / t;
vertices[i] = (0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f);
}
mesh.vertices = vertices;
}
image
code
using UnityEngine;
using System.Collections;
public class PBD_model: MonoBehaviour {
float t= 0.0333f;
float damping= 0.99f;
int[] E;
float[] L;
Vector3[] V;
Vector3 g = new Vector3(0, -9.8f, 0);
float r = 2.7f;
// Use this for initialization
void Start ()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
//Resize the mesh.
int n=21;
Vector3[] X = new Vector3[n*n];
Vector2[] UV = new Vector2[n*n];
int[] T = new int[(n-1)*(n-1)*6];
for(int j=0; j<n; j++)
for(int i=0; i<n; i++)
{
X[j*n+i] =new Vector3(5-10.0f*i/(n-1), 0, 5-10.0f*j/(n-1));
UV[j*n+i]=new Vector3(i/(n-1.0f), j/(n-1.0f));
}
int t=0;
for(int j=0; j<n-1; j++)
for(int i=0; i<n-1; i++)
{
T[t*6+0]=j*n+i;
T[t*6+1]=j*n+i+1;
T[t*6+2]=(j+1)*n+i+1;
T[t*6+3]=j*n+i;
T[t*6+4]=(j+1)*n+i+1;
T[t*6+5]=(j+1)*n+i;
t++;
}
mesh.vertices = X;
mesh.triangles = T;
mesh.uv = UV;
mesh.RecalculateNormals ();
//Construct the original edge list
int[] _E = new int[T.Length*2];
for (int i=0; i<T.Length; i+=3)
{
_E[i*2+0]=T[i+0];
_E[i*2+1]=T[i+1];
_E[i*2+2]=T[i+1];
_E[i*2+3]=T[i+2];
_E[i*2+4]=T[i+2];
_E[i*2+5]=T[i+0];
}
//Reorder the original edge list
for (int i=0; i<_E.Length; i+=2)
if(_E[i] > _E[i + 1])
Swap(ref _E[i], ref _E[i+1]);
//Sort the original edge list using quicksort
Quick_Sort (ref _E, 0, _E.Length/2-1);
int e_number = 0;
for (int i=0; i<_E.Length; i+=2)
if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
e_number++;
E = new int[e_number * 2];
for (int i=0, e=0; i<_E.Length; i+=2)
if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
{
E[e*2+0]=_E [i + 0];
E[e*2+1]=_E [i + 1];
e++;
}
L = new float[E.Length/2];
for (int e=0; e<E.Length/2; e++)
{
int i = E[e*2+0];
int j = E[e*2+1];
L[e]=(X[i]-X[j]).magnitude;
}
V = new Vector3[X.Length];
for (int i=0; i<X.Length; i++)
V[i] = new Vector3 (0, 0, 0);
}
void Quick_Sort(ref int[] a, int l, int r)
{
int j;
if(l<r)
{
j=Quick_Sort_Partition(ref a, l, r);
Quick_Sort (ref a, l, j-1);
Quick_Sort (ref a, j+1, r);
}
}
int Quick_Sort_Partition(ref int[] a, int l, int r)
{
int pivot_0, pivot_1, i, j;
pivot_0 = a [l * 2 + 0];
pivot_1 = a [l * 2 + 1];
i = l;
j = r + 1;
while (true)
{
do ++i; while( i<=r && (a[i*2]<pivot_0 || a[i*2]==pivot_0 && a[i*2+1]<=pivot_1));
do --j; while( a[j*2]>pivot_0 || a[j*2]==pivot_0 && a[j*2+1]> pivot_1);
if(i>=j) break;
Swap(ref a[i*2], ref a[j*2]);
Swap(ref a[i*2+1], ref a[j*2+1]);
}
Swap (ref a [l * 2 + 0], ref a [j * 2 + 0]);
Swap (ref a [l * 2 + 1], ref a [j * 2 + 1]);
return j;
}
void Swap(ref int a, ref int b)
{
int temp = a;
a = b;
b = temp;
}
void Strain_Limiting()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
Vector3[] vertices = mesh.vertices;
//Apply PBD here.
Vector3[] sum_x = new Vector3[vertices.Length];
int[] num_x = new int[vertices.Length];
for(int i=0; i<vertices.Length; i++)
{
sum_x[i] = new Vector3(0, 0, 0);
num_x[i] = 0;
}
for(int ei = 0; ei < L.Length; ei++)
{
int i = E[ei * 2];
int j = E[ei * 2 + 1];
Vector3 xi_xj = vertices[i] - vertices[j];
float len_ij = L[ei] / xi_xj.magnitude;
sum_x[i] += (vertices[i] + vertices[j] + len_ij * (xi_xj)) / 2;
sum_x[j] += (vertices[i] + vertices[j] - len_ij * (xi_xj)) / 2;
num_x[i]++;
num_x[j]++;
}
for(int i=0; i<vertices.Length; i++)
{
if (i == 0 || i == 20) continue;
V[i] += ((0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f) -
vertices[i]) / t;
vertices[i] = (0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f);
}
mesh.vertices = vertices;
}
void Collision_Handling()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
Vector3[] X = mesh.vertices;
//For every vertex, detect collision and apply impulse if needed.
GameObject sphere = GameObject.Find("Sphere");
Vector3 c = sphere.transform.position;
//Handle colllision.
for (int i = 0; i < X.Length; i++)
{
if (i == 0 || i == 20) continue;
float distance = (X[i] - c).magnitude;
if (distance < r)
{
V[i] += (c + r * (X[i] - c) / distance - X[i]) / t;
X[i] = c + r * (X[i] - c) / distance;
}
}
mesh.vertices = X;
}
// Update is called once per frame
void Update ()
{
Mesh mesh = GetComponent<MeshFilter> ().mesh;
Vector3[] X = mesh.vertices;
for(int i=0; i<X.Length; i++)
{
if(i==0 || i==20) continue;
//Initial Setup
V[i] += g * t;
V[i] *= damping;
X[i] += t * V[i];
}
mesh.vertices = X;
for(int l=0; l<32; l++)
Strain_Limiting ();
Collision_Handling ();
mesh.RecalculateNormals ();
}
}
---------------------------我的天空里没有太阳，总是黑夜，但并不暗，因为有东西代替了太阳。虽然没有太阳那么明亮，但对我来说已经足够。凭借着这份光，我便能把黑夜当成白天。我从来就没有太阳，所以不怕失去。
--------《白夜行》
