小师叔
随笔 - 942,  文章 - 0,  评论 - 37,  阅读 - 54万
GAMES 103 动画基础作业1 Shape Matching 浅浅解析

简介

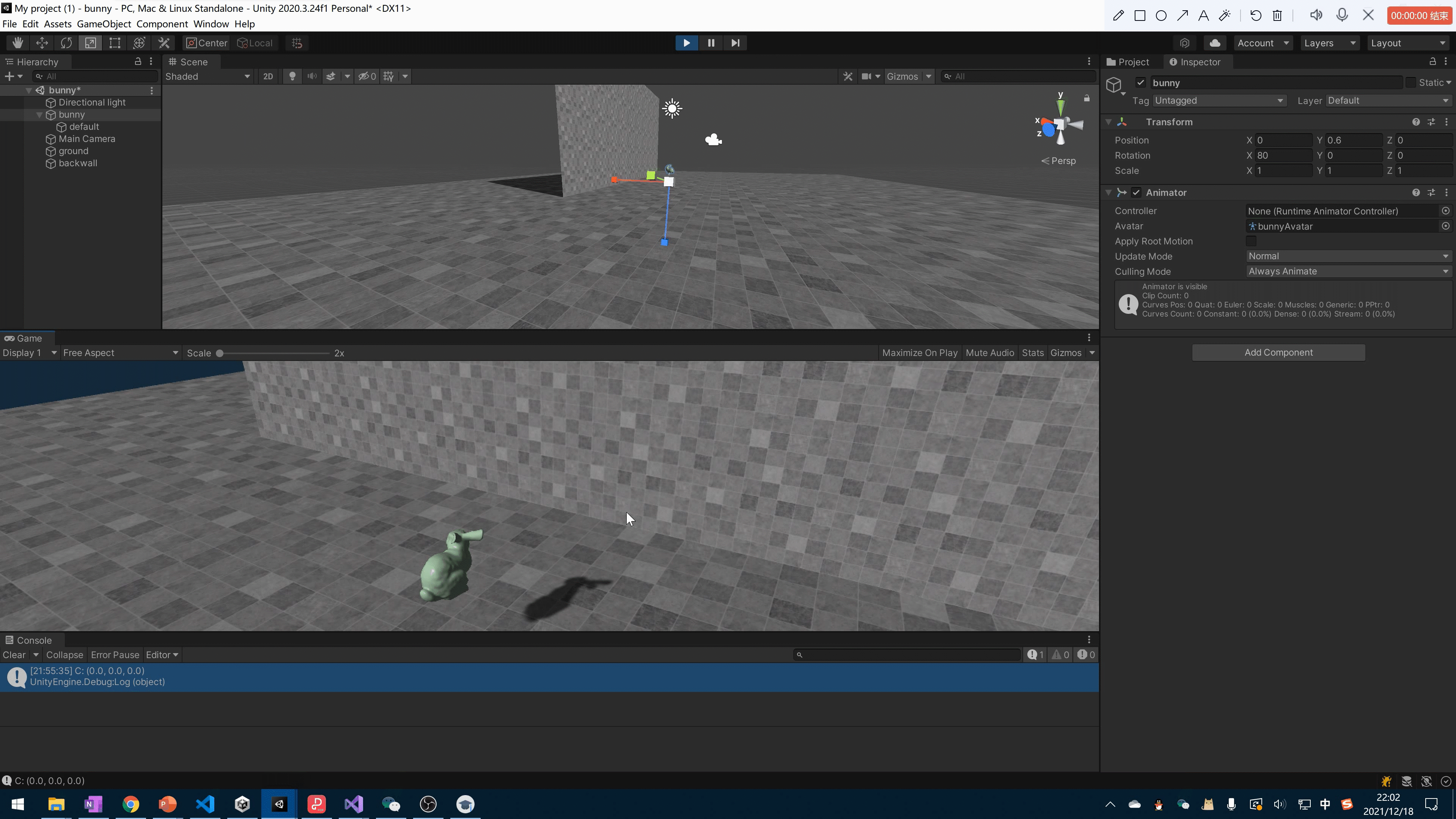
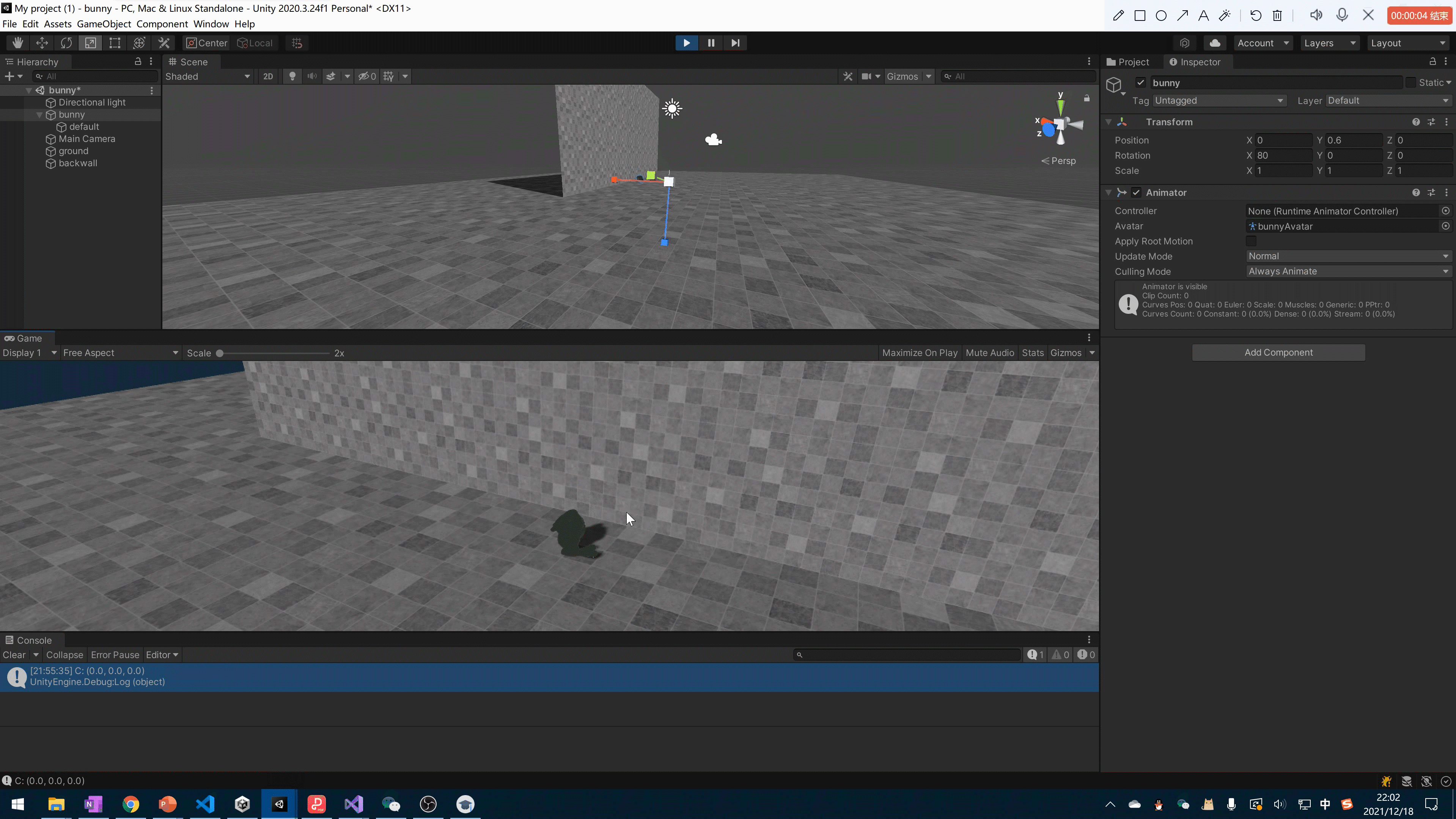
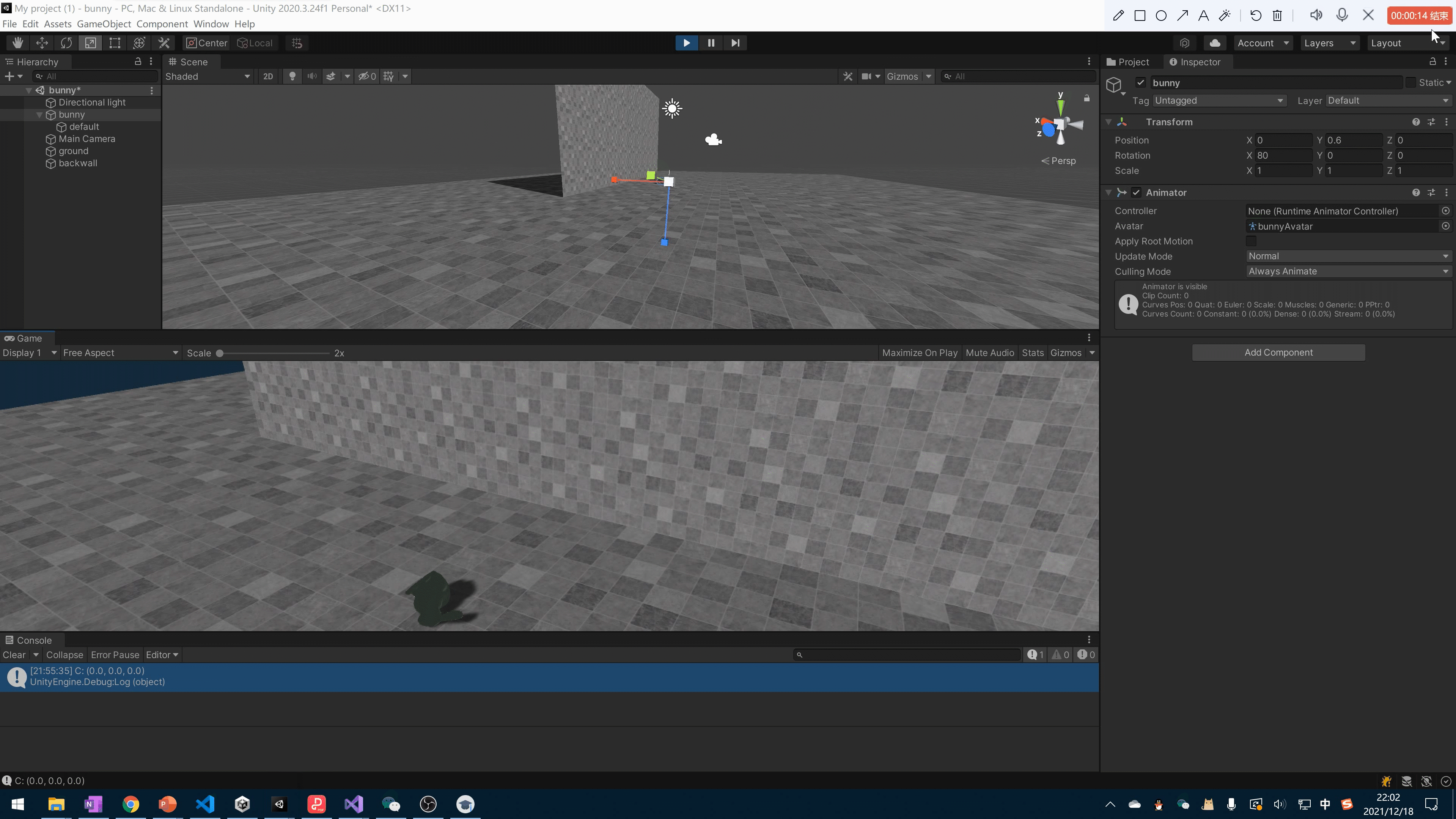
作业1简单实现了一个以一定初始速度和角速度的模型和墙壁碰撞的效果.
总共讲解了三种算法

  1. impulse (脉冲法)

  2. Shape Matching(基于形状保持的算法, 不包含物理特性)

  3. Penalty methods

Shape Matching 可以说是最简单的方法之一

因为完全不涉及角速度. 基础逻辑理论就是, 当模型和墙壁发生碰撞的时候.这些碰撞的粒子会产生相反的形变但是. 我们强制将其整理保持形状的一致性. 就是先形变. 再变回来.
由于形变的步骤. 是中间步骤. 不会展示出来. 所以效果还是挺好的.

Image



TIPS

code

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Rigid_Bunny_by_Shape_Matching : MonoBehaviour
{
	public bool launched = false;
	Vector3[] X; // world position
	Vector3[] Y; // temp world position
	Vector3[] Q; // Local coordinates
	Vector3[] V; // speed
	Vector3[] OldX;
	Matrix4x4 QQt = Matrix4x4.zero;
	Vector3 G = new Vector3(0.0f, -9.8f, 0.0f);
	float linear_decay = 0.999f;
	Vector3 ground = new Vector3(0, 0.01f, 0);
	Vector3 groundNormal = new Vector3(0, 1, 0);
	Vector3 wall = new Vector3(2.01f, 0, 0);
	Vector3 wallNormal = new Vector3(-1, 0, 0);
	float mu_T = 0.5f;  // μ_T may be coefficient of air resistance
	float mu_N = 5.0f; // μ_N may be Coefficient of Restitution
	float m_timer = 0;


	// Start is called before the first frame update
	void Start()
    {
    	Mesh mesh = GetComponent<MeshFilter>().mesh;
        V = new Vector3[mesh.vertices.Length];
        X = mesh.vertices;
		Y = mesh.vertices;
		OldX = mesh.vertices;
        Q = mesh.vertices;

        //Centerizing Q.
        Vector3 c=Vector3.zero;
        for(int i=0; i<Q.Length; i++)
        	c+=Q[i];
        c/=Q.Length;
		Debug.Log("C: " + c);
        for(int i=0; i<Q.Length; i++)
        	Q[i]-=c;

        //Get QQ^t ready.
		for(int i=0; i<Q.Length; i++)
		{
			QQt[0, 0]+=Q[i][0]*Q[i][0];
			QQt[0, 1]+=Q[i][0]*Q[i][1];
			QQt[0, 2]+=Q[i][0]*Q[i][2];
			QQt[1, 0]+=Q[i][1]*Q[i][0];
			QQt[1, 1]+=Q[i][1]*Q[i][1];
			QQt[1, 2]+=Q[i][1]*Q[i][2];
			QQt[2, 0]+=Q[i][2]*Q[i][0];
			QQt[2, 1]+=Q[i][2]*Q[i][1];
			QQt[2, 2]+=Q[i][2]*Q[i][2];
		}
		QQt[3, 3]=1;

		for(int i=0; i<X.Length; i++)
			V[i][0]=4.0f;

		Update_Mesh(transform.position, Matrix4x4.Rotate(transform.rotation), 0);
		transform.position=Vector3.zero;
		transform.rotation=Quaternion.identity;
   	}

	Matrix4x4 vector3x1dotvector1x3(Vector3 A, Vector3 B)
    {
		Matrix4x4 rlt = Matrix4x4.zero;
		rlt[3, 3] = 1.0f;

		rlt[0, 0] = A[0] * B[0];
		rlt[0, 1] = A[0] * B[1];
		rlt[0, 2] = A[0] * B[2];

		rlt[1, 0] = A[1] * B[0];
		rlt[1, 1] = A[1] * B[1];
		rlt[1, 2] = A[1] * B[2];

		rlt[2, 0] = A[2] * B[0];
		rlt[2, 1] = A[2] * B[1];
		rlt[2, 2] = A[2] * B[2];

		return rlt;
    }

   	// Polar Decomposition that returns the rotation from F.
   	Matrix4x4 Get_Rotation(Matrix4x4 F)
	{
		Matrix4x4 C = Matrix4x4.zero;
	    for(int ii=0; ii<3; ii++)
	    for(int jj=0; jj<3; jj++)
	    for(int kk=0; kk<3; kk++)
	        C[ii,jj]+=F[kk,ii]*F[kk,jj];
	   
	   	Matrix4x4 C2 = Matrix4x4.zero;
		for(int ii=0; ii<3; ii++)
	    for(int jj=0; jj<3; jj++)
	    for(int kk=0; kk<3; kk++)
	        C2[ii,jj]+=C[ii,kk]*C[jj,kk];
	    
	    float det    =  F[0,0]*F[1,1]*F[2,2]+
	                    F[0,1]*F[1,2]*F[2,0]+
	                    F[1,0]*F[2,1]*F[0,2]-
	                    F[0,2]*F[1,1]*F[2,0]-
	                    F[0,1]*F[1,0]*F[2,2]-
	                    F[0,0]*F[1,2]*F[2,1];
	    
	    float I_c    =   C[0,0]+C[1,1]+C[2,2];
	    float I_c2   =   I_c*I_c;
	    float II_c   =   0.5f*(I_c2-C2[0,0]-C2[1,1]-C2[2,2]);
	    float III_c  =   det*det;
	    float k      =   I_c2-3*II_c;
	    
	    Matrix4x4 inv_U = Matrix4x4.zero;
	    if(k<1e-10f)
	    {
	        float inv_lambda=1/Mathf.Sqrt(I_c/3);
	        inv_U[0,0]=inv_lambda;
	        inv_U[1,1]=inv_lambda;
	        inv_U[2,2]=inv_lambda;
	    }
	    else
	    {
	        float l = I_c*(I_c*I_c-4.5f*II_c)+13.5f*III_c;
	        float k_root = Mathf.Sqrt(k);
	        float value=l/(k*k_root);
	        if(value<-1.0f) value=-1.0f;
	        if(value> 1.0f) value= 1.0f;
	        float phi = Mathf.Acos(value);
	        float lambda2=(I_c+2*k_root*Mathf.Cos(phi/3))/3.0f;
	        float lambda=Mathf.Sqrt(lambda2);
	        
	        float III_u = Mathf.Sqrt(III_c);
	        if(det<0)   III_u=-III_u;
	        float I_u = lambda + Mathf.Sqrt(-lambda2 + I_c + 2*III_u/lambda);
	        float II_u=(I_u*I_u-I_c)*0.5f;
	        
	        
	        float inv_rate, factor;
	        inv_rate=1/(I_u*II_u-III_u);
	        factor=I_u*III_u*inv_rate;
	        
	       	Matrix4x4 U = Matrix4x4.zero;
			U[0,0]=factor;
	        U[1,1]=factor;
	        U[2,2]=factor;
	        
	        factor=(I_u*I_u-II_u)*inv_rate;
	        for(int i=0; i<3; i++)
	        for(int j=0; j<3; j++)
	            U[i,j]+=factor*C[i,j]-inv_rate*C2[i,j];
	        
	        inv_rate=1/III_u;
	        factor=II_u*inv_rate;
	        inv_U[0,0]=factor;
	        inv_U[1,1]=factor;
	        inv_U[2,2]=factor;
	        
	        factor=-I_u*inv_rate;
	        for(int i=0; i<3; i++)
	        for(int j=0; j<3; j++)
	            inv_U[i,j]+=factor*U[i,j]+inv_rate*C[i,j];
	    }
	    
	    Matrix4x4 R=Matrix4x4.zero;
	    for(int ii=0; ii<3; ii++)
	    for(int jj=0; jj<3; jj++)
	    for(int kk=0; kk<3; kk++)
	        R[ii,jj]+=F[ii,kk]*inv_U[kk,jj];
	    R[3,3]=1;
	    return R;
	}

	// Update the mesh vertices according to translation c and rotation R.
	// It also updates the velocity.
	void Update_Mesh(Vector3 c, Matrix4x4 R, float inv_dt)
   	{
   		for(int i=0; i<Q.Length; i++)
		{
			Vector3 x=(Vector3)(R*Q[i])+c;

			V[i] = (x-X[i])*inv_dt;
			X[i] = x;
		}	
		Mesh mesh = GetComponent<MeshFilter>().mesh;
		mesh.vertices=X;
   	}

	void Collision(float inv_dt)
	{
		for(int i=0; i<Q.Length; i++)
        {
			if(Vector3.Dot(X[i] - ground, groundNormal) < 0 && Vector3.Dot(V[i], groundNormal) < 0)// collision with ground
            {
				Vector3 VN = Vector3.Dot(V[i], groundNormal) * groundNormal;
				Vector3 VT = V[i] - VN;
				float a = Mathf.Max(0, 1.0f - mu_T * (1.0f + mu_N)) * Vector3.Magnitude(VN) / Vector3.Magnitude(VT);
				V[i] = -1.0f * mu_N * VN + 2.0f * a * VT;
            }
			else if(Vector3.Dot(X[i] - wall, wallNormal) < 0 && Vector3.Dot(V[i], wallNormal) < 0) // collision with wall
            {
				Vector3 VN = Vector3.Dot(V[i], wallNormal) * wallNormal;
				Vector3 VT = V[i] - VN;
				float a = Mathf.Max(0, 1.0f - mu_T * (1.0f + mu_N)) * Vector3.Magnitude(VN) / Vector3.Magnitude(VT);
				V[i] = -1.0f * mu_N * VN + 2.0f * a * VT;
			}
        }
	}

    // Update is called once per frame
    void Update()
    {

		if (Input.GetKey("l"))
        {
			launched = true;
			for(int i=0; i<V.Length; i++)
            {
				V[i] = new Vector3(5.0f, 2.0f, 0.0f);
			}
        }
		if (Input.GetKey("r"))
		{
			launched = false;
			for (int i = 0; i < V.Length; i++)
			{
				V[i] = new Vector3(4.0f, 0.0f, 0.0f);
			}

			Update_Mesh(new Vector3(0, 0.6f, 0), Matrix4x4.Rotate(transform.rotation), 0);
		}
		if(!launched)
        {
			return;
        }
		//m_timer += Time.time;
		//if (m_timer <= 500)
		//{
		//	return;
		//}
		//else
		//{
		//	m_timer = 0;
		//}


		float dt = 0.015f;

  		//Step 1: run a simple particle system.
        for(int i=0; i<V.Length; i++)
        {
			V[i] = V[i] + G * dt;
			V[i] *= linear_decay;
        }

        //Step 2: Perform simple particle collision.
		Collision(1/dt);

		// Step 3: Use shape matching to get new translation c and 
		// new rotation R. Update the mesh by c and R.
        //Shape Matching (translation)
		for(int i=0; i<V.Length; i++)
        {
			Y[i] = X[i] + V[i] * dt;
        }

		// calc c
		Vector3 c = new Vector3(0, 0, 0); 
		for(int i=0; i<V.Length; i++)
        {
			c += Y[i];
        }
		c = c / V.Length;

		// calc A
		Matrix4x4 A = Matrix4x4.zero;
		A[3, 3] = 1.0f;
		for (int i=0; i<V.Length; i++)
        {
			Matrix4x4 o = vector3x1dotvector1x3(Y[i] - c, Q[i]);
			A[0, 0] += o[0, 0];
			A[0, 1] += o[0, 1];
			A[0, 2] += o[0, 2];
			A[1, 0] += o[1, 0];
			A[1, 1] += o[1, 1];
			A[1, 2] += o[1, 2];
			A[2, 0] += o[2, 0];
			A[2, 1] += o[2, 1];
            A[2, 2] += o[2, 2];
		}
		A = A * QQt.inverse;

		//Shape Matching (rotation)
		// calc R
		Matrix4x4 R = Matrix4x4.zero;
		R = Get_Rotation(A);

		Update_Mesh(c, R, 1/dt);

	}
}

TRICK

PIPELINE

计算 C (模型质心坐标)

计算 A (通过A计算得到R, 即 旋转矩阵) == 从A得到R. 老师已经提供了.

更新顶点坐标

Trick

在处理碰撞的函数中. 里面的参数是自己调整的参数. 比如 5.0f 逻辑上 μ_T μ_N 都应该是一个小于1的数. 但是, 测试后感觉效果不是特别好. 如果你知道为什么的话, 请留言.

请看完bilibli 4个视屏后开始自己的作业.

参考链接

配置VS 作为 Unity 的配置环境
https://blog.csdn.net/qq_34405576/article/details/105572069

源码参考师弟写出来的, 大部分是抄的嘿嘿~~ 侵权删除.

posted on   HDU李少帅  阅读(906)  评论(0)  编辑  收藏  举报
编辑推荐：
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列：如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列：如何用 C#调用 C方法造成内存泄露
阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· Manus爆火，是硬核还是营销？
· 终于写完轮子一部分：tcp代理 了，记录一下
· 别再用vector＜bool＞了！Google高级工程师：这可能是STL最大的设计失误
· 单元测试从入门到精通
历史上的今天：
2017-12-18 LInux main.cpp 编码问题 导致影响后面的内容

< 2025年3月 >
日 一 二 三 四 五 六
23 24 25 26 27 28 1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30 31 1 2 3 4 5
Copyright © 2025 HDU李少帅
Powered by .NET 9.0 on Kubernetes Powered By博客园
点击右上角即可分享
微信分享提示