简介
将粗四边形映射到原网格 3.5 Coarse Quad Layout and Mapping 精读
\(Q\) 表示粗四边形网格
\(\mathcal{M}\) 表示原始的三角形网格
为了总结我们的计算管线,我们需要去计算了一个参数化从\(\mathcal{M}\)映射到\(Q\),也就是说,定一个一个bijective mapping(听Games102的课这个表示一个全局映射,无重叠无交错)在这两个之上。为了这么做,我们设定每个在\(\mathcal{M}\)上的点\(v\)得到一个在\(Q\)上的位置,这个位置被在\(Q\)上的四边形\(q_i\)和一对参数化坐标(归一化到\([0,1]\times[0,1]\)。)在\(q_i\)上。将每个在\(\mathcal{M}\)上的顶点映射到一个四边形区域。
其中,\(Q\)上的边由映射到\(\mathcal{M}\)上,所映射的边一般不是\(\mathcal{M}\)上原有的边。同样的在\(Q\)上的点,映射到\(\mathcal{M}\)上一般不是\(\mathcal{M}\)上的点。
最终的映射由两部分组成:
- 我们计算一个粗任务通过投影\(Q\)到\(\mathcal{M}\)上。
- 我们提升投影的效果通过交错迭代处理修成和缩放。
3.5.1 初始化映射
粗映射不需要很精确:粗映射可以包含重叠,扭曲,和在\(\mathcal{M}\)上的区域边界次优化的位置。
我们通过以下方式处理。
Skeleton “fattening”. 骨架变胖?(什么鬼,感觉就是粗骨架呀??)
一个嵌入的\(Q\)被获得通过方式\(Q\)的盒中心在曲线骨架上,将它们的朝向重新放置通过上面描述的步骤(就是最小化一个能量啥的),和将它们缩放通过关键球的半径;万一我们没有关键球的半径,那么我们将关键六面体的和大小通过估算骨架的节点到\(\mathcal{M}\)上的最近的点;这创建了一个粗骨架。
Initial projection 初始化投影
每个在\(Q\)上的点投影到\(\mathcal{M}\)上沿着表面法向量估计从变肥的骨架上平均邻面,如果投影失败,在\(\mathcal{M}\)上的最近点被选中(应该是从Q上的点到\(\mathcal{M}\)上的最近点)。QU:但是正常投影的步骤不太清楚,那句话读的不太明白。
Subdivision 细分
每个\(q_i\)在\(Q\)上的面,迭代细分通过CC细分方案,获得对应的网格子主要区域\(q_i\);在每个迭代细分处理,新创建的顶点通过上面的步骤投影到\(\mathcal{M}\)。
Back-projection. 逆向投影
\(\mathcal{M}\)投影到每个\(q_i\),使用上面相同的策略。
最后我们溢出了变循环沿着管道结构,从现在开始,\(Q\)的结合不再相关:在以后的处理进程中,\(Q\)被考研仅仅作为一个2D的长方形,使用邻接信息完成。在这种意义上我们的主区域\(Q\)是抽象的,被定义在Pietroni et al.[2010].
3.5.2 提升细节
\(\mathcal{M}\)上的点和边的布局,也解决了重叠在初始化映射的时候产生的问题。这个步骤很接近之前文章提出来的细节 [in the second part of Tarini et al. 2011][Campen and Kobbelt 2014b].
程序包括迭代松弛\(Q\)投影到\(\mathcal{M}\)上的点,在每个迭代过程中,\(Q\)被分割在一系列“宏观区域”,每一个有一些小的组(临近的四边形\(Q\)中的)有类瓷盘拓扑(QU:是什么鬼),一个宏观区域被一些点在\(Q\)上的一邻域组成。在么个区域的参数化通过平均值参数化进行优化 [Floater 2003]这篇文章有所提及。且保持边节点固件。特定地,我们冻结了所有三角形的顶点。在最后的迭代过程中,宏观区域,被分解回原来的四边形。注意到将\(\mathcal{M}\)上的点移动到了在不同的\(Q\)上的四边形。
不同的组合被使用在每个迭代过程中。如图所示,看这张图可以比较简单的看出来什么是宏观区域。
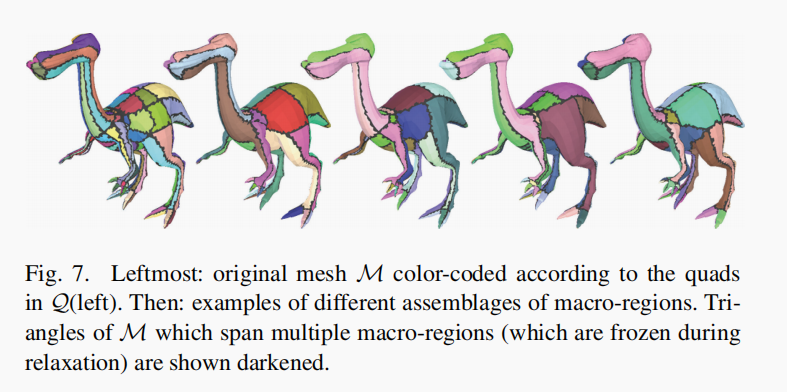
随意每个点在\(\mathcal{M}\)上最后都经历优化,在每个迭代过程中满足一个贪心算法:
我们组建增加四边形到宏观区域知道没有四边形剩下;对于每个点和每个在\(Q\)上的边,我们保持追溯最后的迭代在元素经历了松弛。首先我们组赚了一个额定点宏观区域,开始从一个构建在\(Q\)的的点点周围,有冰洁在边界对于大部分的迭代;
剩下的四边形被组装进了边的宏观区域,以相同的标准进行有限排序;最后,单独的四边形形成面宏观区域。(QU:有点看不懂了。)
松弛表现在宏观区域的内部也保留了为了展开折叠区域的目的:如果必要,这个可以被加入到线性约束中,在[Bommes
et al. 2013a].文章之后。没有保证每个折叠区域会落在一个完整的宏观区域内部,但是在我们的实验中,我们没有遇到任何失败的案例。如果需要提升,ad-hoc 可以很容易的将上述实现。
在 Khodakovsky et al. [2003] 之后,一个顶点的宏观区域构成围绕着在\(Q\)上的不规则点,四边形被转化通过一个指数映射为了去将它们摊平在平面上。虽然这个映射是连续的情况下式完全共形的,他可以偶尔增加共形能量,或者引入新的折叠区域,由于离散的网格区域;这是一个镜像技术困难可以总是解决一个局部和临时的修正\(\mathcal{M}\);更多的实际遇到的措施,我们使用的,包括冻结或者滚动回信创建的这折叠三角形和滚回松弛处理可以导致一个全局增加共形能量,我们停止处理直到增加的全局共形能量没有超过了预先设定的门限。每一个迭代不能增加总共形能量,被保留通过所有的映射去和来自宏观区域,保证了趋同(QU:什么鬼?)
3.5.3 缩放
我们使用了一个额外的优化,与前面的交织在一起,去决定构想四边形在\(Q\)上显像管的大小。这将是有用的,为了之后提取半圆形四边形网格(4.1参照)
首先,为每个四边形\(q_i\)扎到理想的比率\(r_i\),最小化共形能量Levy et al. [2002].提出的共形能量。这个子问题通过最近的每个内部三角形和每个四边形的面积均值来解决。
然后,我们找到了一个全局一致分配对于四边形的场合宽,回忆,在我们抽象的区域,一个相邻定义在两个一对四边形意味着他们的长度相等。我们构建了一个系统,每个变量\(v_1,v_n\)对应于每个四边形的宽度或者长度,我们减少了一些列的变量带有这些质量。如果一个四边形\(q_i\)是\(v_w\)宽度和\(v_h\)高度,我们想要 \(v_w/v_h=r_i\)被我们重写为\(\log v_w - \log v_h = \log r_i\)。我们接对应的超定线性方程在最小二乘方法去恢复变量的logs值,因此宽度合高度对应于每个四边形。


