模拟退火 python 实现

简介

一直以为是一个高深的算法，好像据说在量子计算机中可以应用。发现原理并不难

参考链接

https://blog.csdn.net/google19890102/article/details/45395257
https://blog.csdn.net/wfrainn/article/details/80303138

算法缺点

这个算法怎么感觉概率的地方基本不受控制，温度降到最后还是大量接受随机解？
模拟退火就是这样的，因为它到了最优解过后还能跳出最优解域，因此能找到别的解域的最优解的值。因此一定要记录下历史最优解。

算法流程图

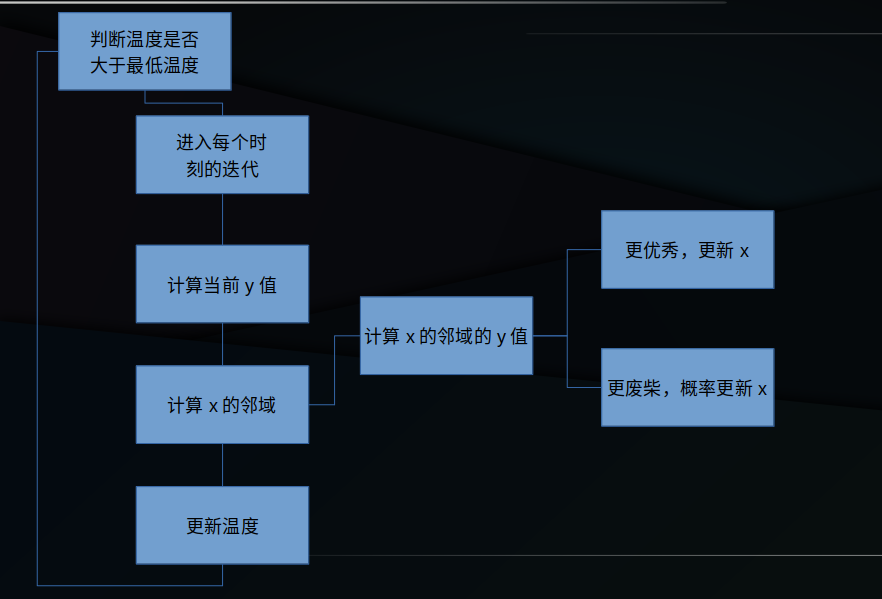
code

对https://blog.csdn.net/wfrainn/article/details/80303138进行的代码更新

result

直接输出 39.72958243492729 -32148.550564632504
记录最小数值 40.033185051881034 -32154.066628802473

发现保留的最小值确实更接近最小值
code

#coding=utf-8
import numpy as np
from monituihuo import aimFunction
import math
T=1000 # initiate temperature
Tmin=10 # minimun value of terperature
x = np.random.uniform(low=0, high=100) # initiate x
k=50 # times of internal circulation
y = 0 # initiate result
t=0 # time
xmin = 100
ymin = 100 # 观察凸显给出的数值
while T>Tmin:
    for i in range(k):
        y=aimFunction(x)
        # generate a new x in the neighboorhood of x by transform function
        xNew = x + np.random.uniform(low=-0.055, high=0.055) * T
        if(0<=xNew and xNew <=100):
            yNew=aimFunction(xNew)
            if(yNew - y <= 0):
                x = xNew
                if(yNew < ymin):
                    xmin = x
                    ymin = yNew
            else:
                #metropolis principle
                p = math.exp(-(yNew-y) / T)
                r = np.random.uniform(low=0, high=1)
                if r < p:
                    x=xNew
    t+=1
    # print(t)
    T=(1000)/(1+t)
print('直接输出',x, aimFunction(x))
print('记录最小数值',xmin, aimFunction(xmin))

#coding=utf-8  
from __future__ import division # 将新版本的特性引入
import numpy as np
import matplotlib.pyplot as plt
import math

def aimFunction(x):
    y=x**3-60*x**2-4*x+6
    return y

x = [i/10 for i in range(1000)]
y = [0 for i in range(1000)]
for i in range(1000):
    y[i] = aimFunction(x[i])
plt.plot(x,y)
# plt.show()