网格简化

简介

网格简化是图形学中的一项重要操作，可以加深对于图形学的理解

论文

Surface Simplification Using Quadric Error Metrics

实现步骤

算法思路：

1. 计算每一个点的 Kp 矩阵

\[K_{p}=\left(\begin{array}{llll} a^{2} & a b & a c & a d \\ a b & b^{2} & b c & b d \\ a c & b c & c^{2} & c d \\ a d & b d & c d & d^{2} \end{array}\right)\]

2建立最小堆 使用 multiset 建立
3.迭代
a.移动顶点
b.删除顶点
c.增加面

TIPS

1.

\[\begin{aligned} \Delta(\mathbf{v}) &=\sum_{\mathbf{p} \in \operatorname{planes}(\mathbf{v})}\left(\mathbf{v}^{\top} \mathbf{p}\right)\left(\mathbf{p}^{\top} \mathbf{v}\right) \\ &=\sum_{\mathbf{p} \in \text { planes }(\mathbf{v})} \mathbf{v}^{\top}\left(\mathbf{p} \mathbf{p}^{\top}\right) \mathbf{v} \\ &=\mathbf{v}^{\top}\left(\sum_{\mathbf{p} \in \text { planes }(\mathbf{v})} \mathbf{K}_{\mathbf{p}}\right) \mathbf{v} \end{aligned}\]

上式 其实就是 Q 二次误差的计算方式

2.

\[\overline{\mathbf{v}}=\left[\begin{array}{cccc} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{12} & q_{22} & q_{23} & q_{24} \\ q_{13} & q_{23} & q_{33} & q_{34} \\ 0 & 0 & 0 & 1 \end{array}\right]^{-1}\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]\]

为什么这样可以得到 两个点之间 二次误差最小的点呢？

我的理解

因为$$v^{T} K_{p} v=Q$$假设Q是0那说明是不是误差最小呢？是的
那么

\[K_{p} v=0 *\left(v^{T}\right)^{-1}=\left(\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right)\]

若\(K_p\) 正定那么

\[v=\left(\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right) *\left(K_{p}\right)^{-1} \]

3.

关于为啥二次误差有用

我的理解

\(v^T * p\) 表示的是一个顶点 带入 面的方程 ax + by + cz + d = Q Q就表示偏差 如果Q等于0那么就表示这个顶点就在面上，不会产生误差

4.

论文的启发点，其实就是利用了 ax + by + cz + d = Q 的性质，然后计算的快些，然后就可以简化发论文了，所以，发论文好难......

结果图片

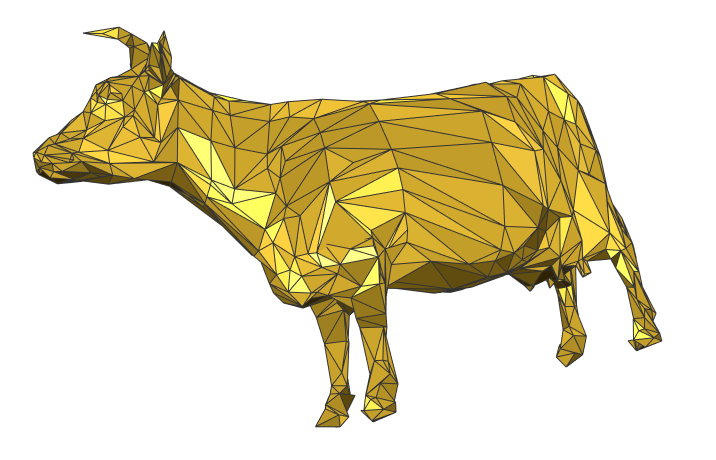
是不是很有感jio？？？jojo

code

https://github.com/lishaohsuai/digital_geo/tree/master/Surface_Framework_VS2017

参考文献

https://www.cnblogs.com/shushen/p/5311828.html