以下内容来自网课 数据结构与算法基础(青岛大学-王卓),结合一些博客作出总结,代码来自网络与一些书籍
相互交流,共同进步
数据结构
基本概念与术语
-
数据(Data)是客观事物的符号表示,是所有能输入到计算机中并被计算机程序处理的符号的总称(集合)。是信息的载体;是对客观事物的符号化表示;可以被计算机识别、存储和加工。数据不仅仅包含整型、实型等数值类型,还包含图形、图像、声音、视频及动画等非数值类型
对于整型、实型等数值类型,可以进行数值计算;
对于字符数据类型,就需要进行非数值的处理。
而声音、图像、视频等其实是可以通过编码的手段变成字符数据来处理的。
-
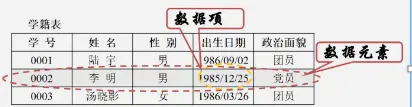
数据元素(DataElement)是数据的基本单位,在计算机中通常作为一个整体进行考虑和理。在有些情况下,数据元素也称为元素、记录、节点、顶点等。如前一节示例中的一名学生记录,树中棋盘的一个格局(状态),以及图中的一个顶点等。
-
数据项(Data Item)是组成数据元素的、有独立含义的、不可分割的最小单位。例如,学生基本信息表中的学号、姓名、性别等都是数据项。【数据项是“数据的最小单位。但真正讨论问题时,数据元素才是数据结构中建立数据模型的着眼点。就像我们讨论一部电影时,是讨论这部电影角色这样的数据元素”,而不是针对这个角色的姓名或者年龄这样的“数据项”去研究分析。】
-
数据对象(DataObject)是性质相同的数据元素的集合,是数据的一个子集。例如:整数数据对象是集合N={0, ±1,±2,...}, 字母字符数据对象是集合C={'A','B', ...‘Z’,'a','b', ..., 'z'}, 学生基本信息表也可以是一个数据对象。由此可以看出,不论数据元素集合是无限集(如整数集),或是有限集(如字母字符集),还是由多个数据项组成的复合数据元素(如学生表)的集合,只要集合内元素的性质均相同,都可称之为一个数据对象。
总结:数据是抽象集合的统称,是一个大类,而数据对象是数据的子集,但仍然是一个类,而数据元素可以看作组成对象的基本单位,而每个数据元素由数据项组成。
数据结构
结构
简单的理解就是关系,比如分子结构,就是说组成分子的原子之间的排列方式。严格点说,结构是指各个组成部分相互搭配和排列的方式。在现实世界中,不同数据元素之间不是独立的,而是存在特定的关系,我们将这些关系称为结构。那数据结构是什么?
数据结构(Data Structure)是相互之间存在一种或多种特定关系的数据元素的集合。换句话说,数据结构是带”结构"的数据元素的集合,“结构”就是指数据元素之间存在的关系。
数据结构分两个层次 :逻辑结构和物理结构。
逻辑结构和物理结构
- 逻辑结构
数据的逻辑结构是从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。数据的逻辑结构有两个要素:一是数据元素;二是关系。
基于逻辑结构进行分类,有两种分类方法:
第一类:
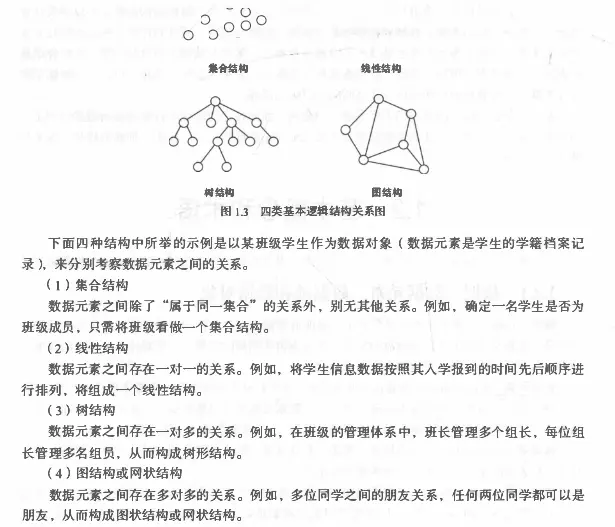
- 线性结构:有且仅有一个开始和一个终端结点,并且所有结点都最多只有一个直接前趋和一个直接后继。
- 非线性结构:一个结点可能有多个直接前趋和直接后继例如:树、图
第二类(如下图):
- 物理结构
数据的物理结构是数据元素及其关系在计算机存储器中的结构(存储方式),是数据结构在计算机中的表示。
四种基本储存结构分类如下
- 顺序存储结构:用一组连续的存储单元依次存储数据元素,数据元素之间的逻辑关系由元素的存储位置来表示。(eg.:数组)
- 链式存储结构:用一组任意的存储单元存储数据元素,数据元素之间的逻辑关系用指针来表示。(eg.:链表)
- 索引存储结构
- 在存储结点信息的同时,还建立附加的索引表。
- 索引表中的每一项称为一个索引项。
- 索引项的一般形式是:关键字/地址
- 关键字是能唯一标识一个结点的那些数据项。
- 若每个结点在索引表中都有一个索引项,则该索引表称之为稠密索引(Dense Index)。
- 若一组结点在索引表中只对应一个索引项,则该索引表称之为稀疏索引(Sparse Index)。
- 散列存储结构:·根据结点的关键字直接计算出该结点的存储地址。
- 逻辑结构与物理结构间的关系:
存储结构是逻辑结构关系的映象与元素本身的映象。
逻辑结构是数据结构的抽象,存储结构是数据结构的实现。
两者综合起来建立了数据元素之间的结构关系。
数据类型和抽象数据类型
数据类型
说到数据类型其实我们并不陌生,在使用高级程序设计语言编写程序时,必须对程序中出现的每个变量、常量或表达式、C语言中函数的参数、返回值,明确说明它们所属的数据类型。
C语言中:提供int,char,float,double等基本数据类型;数组、结构、共用体、枚举等构造数据类型;还有指针、空(void)类型,用户也可用typedef自己定义数据类型。而另一些常用的数据结构,如栈、队列、树、图等,不能直接用数据类型来表示。
在C语言中,数据类型可以分为两类:
原子类型:是不可以再分解的基本类型,包括整型、实型、字符型等
结构类型:由若干个类型组合而成,是可以再分解的。例如,整型姿型数据组成的数组。
数据类型是一个值的集合和定义在这个值集上的一组操作的总称。
抽象
抽象是从众多的事物中抽取出共同的、本质性的特征,而舍弃其非本质的特征的过程。具体地说,抽象就是人们在实践的基础上,对于丰富的感性材料通过去粗取精、去伪存真、由此及彼、由表及里的加工制作,形成概念、判断、推理等思维形式,以反映事物的本质和规律的方法。
实际上,抽象是与具体相对应的概念,具体是事物的多种属性的总和,因而抽象亦可理解为由具体事物的多种属性中舍弃了若干属性而固定了另一些属性的思维活动。
抽象数据类型
抽象数据类型(Abstract Data Type, ADT)一般指由用户定义的、表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称,具体包括三部分:数据对象、数据对象上关系的集合以及对数据对象的基本操作的集合。
由用户定义,从问题抽象出数据模型(逻辑结构)
还包括定义在数据模型上的一组抽象运算(相关操作)
不考虑计算机内的具体存储结构与运算的具体实现算法
抽象数据类型的形式定义
抽象数据类型可用(D,S,P)三元组表示【离散数学上的概念】其中:

总结
抽象数据类型的概念与面向对象方法的思想是一致的。抽象数据类型独立于具体实现,将数据和操作封装在一起,使得用户程序只能通过抽象数据类型定义的某些操作来访问其中的数据,从而实现了信息隐藏。在C++中,我们可以用类的声明表示抽象数据类型,用类的实现来实现抽象数据类型。因此,C++中实现的类相当于数据的存储结构及其在存储结构上实现的对数据的操作
算法与算法分析
算法定义
解决问题的方法和步骤。在计算机中表现为指令的有限序列。其中每条指令表示一个或多个操作。
程序与算法
- 程序=数据结构+算法
- 数据结构通过算法来实现操作
- 算法根据数据结构设计程序
算法五大特性:
算法的特性(确定、有穷、可行、输入、输出)
- 有穷性:算法在执行有限步骤之后,自动结束而不会出现无限循环,并且每一个步骤都在可接受的时间范围内完成。当然这里的有穷并不是纯数学意义的,而是在实际应用中合理的、可以接受的“边界”。你说你写一个算法,计算机需要算上20年,一定会结束,它在数学上是有穷的,但这多数情况是不符合实际应用的。
- 确定性:算法的每一个步骤都有确定的含义,不会出现二义性(不会有歧义)。
- 可行性:算法中的所有操作都可以通过已经实现的基本操作运算执行有限次来实现。
- 输入:一个算法有零个或多个输入。当用函数描述算法时,输入往往是通过形参表示的,在它们被调用时,从主调函数获得输入值。
- 输出:一个算法有一个或多个输出,它们是算法进行信息加工后得到的结果,无输出的算法没有任何意义。当用函数描述算法时,输出多用返回值或引用类型的形参表示。
算法的设计要求
好的算法应该具有正确性、可读性、健壮性、时间效率高和存储量低的特征。
-
正确性(Correctness):能正确的反映问题的需求,能得到正确的答案
分以下四个层次:
- 算法程序没有语法错误;
- 算法程序对n组输入产生正确的结果;
- 算法程序对典型、苛刻、有***难性的几组输入可以产生正确的结果;(主)
- 算法程序对所有输入产生正确的结果;
但我们不可能逐一的验证所有的输入,因此算法的正确性在大多数情况下都不可能用程序证明,而是用数学方法证明。所以一般情况下我们把层次3作为算法是否正确的标准。
-
可读性(Readability):算法,首先应便于人们理解和相互交流,其次才是机器可执行性。可读性强的算法有助于人们对算法的理解,而难懂的算法易于隐藏错误,且难于调试和修改。
-
健壮性(Robustness):当输入的数据非法时,好的算法能适当地做出正确反应或进行相应处理,而不会产生一些莫名其妙的输出结果。【健壮性又名鲁棒性/robust即使用棒子粗鲁地对待他也可以执行类似于Java预料到可能出现的异常并对其进行捕获处理】
-
高效性(Efficiency):时间效率高和存储量低
算法分析
算法分析的目的是看算法实际是否可行,并在同一问题存在多个算法时可进行性能上的比较,以便从中挑选出比较优的算法。其中常用的两种比较策略为时间复杂度和空间复杂度。
- 算法效率以下两个方面来考虑:
-
时间效率:指的是算法所耗费的时间;
-
空间效率:指的是算法执行过程中所耗费的存储空间。
- 时间效率和空间效率大多时候是矛盾的。
时间复杂度
为了便于比较不同算法的时间效率,我们仅比较它们的数量级。
若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度(О是数量级的符号),简称时间复杂度。
空间复杂度
空间复杂度:算法所需存储空间的度量。
算法本身要占据的空间:输入/输出、指令、常数、变量等。
记作:S(n)=O(f(n))
其中n为问题的规模(或大小)
若输入数据所占据的空间只取决于问题本身和算法无关,这样只需分析该算法在实现时所需的辅助单元即可,若算法执行时所需的辅助单元相对于输入数据量而言是个常数,则称此算法为原地施工,空间复杂度为O(1)。

时间与空间的取舍
人们之所以花大力气去评估算法的时间复杂度和空间复杂度,其根本原因是计算机的运算速度和空间资源是有限的。就如一个大财主,基本不必为日常的花销而伤脑筋,而一个没有多少积蓄的普通人则不得不为日常的花销精打细算。对于计算机系统来说也是如此,虽然目前计算机的CPU处理速度不断飙升,内存和硬盘空间也越来越大,但是面对庞大而复杂的数据和业务,我们仍要精打细算,选择最有效的利用方式。
举个例子说,要判断某年是不是闰年,你可能会花一点心思来写一个算法,每给一个年份,就可以通过这个算法计算得到是否闰年的结果。
另外一种方法是,事先建立一个有2050个元素的数组,然后把所有的年份按下标的数字对应,如果是闰年,则此数组元素的值是1,如果不是元素的值则为0。这样,所谓的判断某一年是否为闰年就变成了查找这个数组某一个元素的值的问题。
第一种方法相比起第二种来说很明显非常节省空间,但每一次查询都需要经过一系列的计算才能知道是否为闰年。第二种方法虽然需要在内存里存储2050个元素的数组,但是每次查询只需要一次索引判断即可。
这就是通过一笔空间上的开销来换取计算时间开销的小技巧。到底哪一种方法好?其实还是要看你用在什么地方。但在绝大多数情况下,时间复杂度更重要一些,我们宁愿多分配一些内存空间也要提升程序的执行速度。
线性表
定义
由n(n≥O)个数据特性相同的元素构成的有限序列称为线性表。

特点
**同一线性表中的元素必定具有相同的特性,数据元素之间关系是线性的 **
结构
- 逻辑结构:
线性表中元素的个数n(n≥O)定义为线性表的长度,n=O时称为空表。
将非空的线性表(n>O)记作(a1,a2,a3,...,an)
这里的数据元素ai(1≤i≤n)只是个抽象的符号,其具体含义在不同情况下可以不同。
在非空的线性表,有且仅有一个开始结点a1,它没有直接前趋,而仅有一个直接后继a2;
有且仅有一个终端结点an,它没有直接后继,而仅有一个直接前趋an-1;
其余的内部结点ai,(2<i<n-1)都有且仅有一个直接前趋ai-1和一个直接后继ai+1
-
存储结构 :
-
顺序
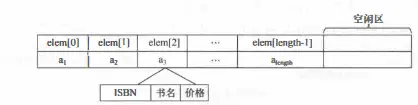
-
链式
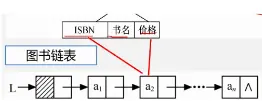
-
代码部分
顺序实现如下(C++):
#include <iostream>
using namespace std;
template<class ElemType>
class SqList {
protected:
// 数据成员
ElemType *elems; //元素储存空间
int maxSize; //顺序表最大元素个数
int count; //元素个数
public:
// 抽象数据类型方法声明及重载编译系统默认方法声明
explicit SqList(int size = 10);
virtual ~SqList();
int Length() const;
bool Empty() const;
void Clear();
void DoubleMax();
void Show();
bool GetElem(int position, ElemType &e) const;
bool SetElem(int position, const ElemType &e);
bool Delete(int position, ElemType &e);
bool Delete(int position);
bool Insert(int position, const ElemType &e);
SqList(const SqList<ElemType> &source);
SqList<ElemType> &operator=(const SqList<ElemType> &source);
};
template<class ElemType>
SqList<ElemType>::SqList(int size) {
maxSize = size;
elems = new ElemType[maxSize];
count = 0;
}
template<class ElemType>
SqList<ElemType>::~SqList<ElemType>() {
delete[]elems;
}
template<class ElemType>
int SqList<ElemType>::Length() const {
return count;
}
template<class ElemType>
bool SqList<ElemType>::Empty() const {
return count == 0;
}
template<class ElemType>
void SqList<ElemType>::Clear() {
count = 0;
}
template<class ElemType>
void SqList<ElemType>::Show() {
for (int i = 0; i < this->Length(); i++) {
cout << this->elems[i] << "\t";
}
cout << endl;
}
template<class ElemType>
void SqList<ElemType>::DoubleMax() {
SqList<ElemType> a(maxSize * 2);
ElemType temp;
for (int i = 0; i < this->Length(); i++) {
this->GetElem(i, temp);
a.SetElem(i, temp);
}
SqList<ElemType> b = *this;
*this = a;
delete[]b.elems;
}
template<class ElemType>
bool SqList<ElemType>::GetElem(int position, ElemType &e) const {
if (position < 0 || position > Length()) {
return false;
} else {
e = elems[position - 1];
return true;
}
}
template<class ElemType>
bool SqList<ElemType>::SetElem(int position, const ElemType &e) {
if (position < 0 || position > Length() - 1) {
return false;
} else {
elems[position] = e;
return true;
}
}
template<class ElemType>
bool SqList<ElemType>::Delete(int position) {
if (position < 0 || position > Length()) {
return false;
} else {
ElemType e;
for (int temp = position + 1; temp < Length() + 1; temp++) {
GetElem(temp, e);
SetElem(temp - 1, e);
}
count--;
return true;
}
}
template<class ElemType>
bool SqList<ElemType>::Delete(int position, ElemType &e) {
if (position < 0 || position > Length()) {
return false;
} else {
GetElem(position, e);
ElemType tempElem;
for (int temp = position + 1; temp < Length() + 1; temp++) {
GetElem(temp, tempElem);
SetElem(temp - 1, tempElem);
}
count--;
return true;
}
}
template<class ElemType>
bool SqList<ElemType>::Insert(int position, const ElemType &e) {
if (position < 0 || position > Length()) {
return false;
} else {
if (count == maxSize) {
DoubleMax();
}
ElemType tempElem;
for (int temp = Length(); temp > position - 1; temp--) {
GetElem(temp, tempElem);
SetElem(temp + 1, tempElem);
}
count++;
SetElem(position, e);
return true;
}
}
template<class ElemType>
SqList<ElemType>::SqList(const SqList<ElemType> &source) {
*this = source;
}
template<class ElemType>
SqList<ElemType> &SqList<ElemType>::operator=(const SqList<ElemType> &source) {
if (&source != this) {
maxSize = source.maxSize;
count = source.count;
elems = new ElemType[maxSize];
for (int temp = 1; temp < source.Length() + 1; temp++) {
elems[temp - 1] = source.elems[temp - 1];
}
}
}
int main() {
SqList<int> a(15);
cout << "当前储存是否为空:" << a.Empty() << endl;
cout << "目前长度为:" << a.Length() << endl;
for (int i = 0; i < 15; i++) {
a.Insert(i, i + 1);
}
cout << "插入后长度为:" << a.Length() << endl;
cout << "输出数据如下:" << endl;
a.Show();
return 0;
}
链式实现如下(C++):
#include<iostream>
using namespace std;
#include<cstring>
//节点
template<class ElemType>
struct DblNode {
ElemType data;
DblNode<ElemType> *back;
DblNode<ElemType> *next;
DblNode();//给初始化链表用
explicit DblNode(const ElemType &e, DblNode<ElemType> *linkBack = nullptr,
DblNode<ElemType> *linkNext = nullptr);//给后面插入赋值用
};
template<class ElemType>
DblNode<ElemType>::DblNode() {
back = next = nullptr;
}
template<class ElemType>
DblNode<ElemType>::DblNode(const ElemType &e, DblNode<ElemType> *linkBack, DblNode<ElemType> *linkNext) {
data = e;
back = linkBack;
next = linkNext;
}
//链表
template<class ElemType>
class DblLinkList {
protected:
DblNode<ElemType> *head;//头
DblNode<ElemType> *tail;//尾
DblNode<ElemType> *GetElemPtr(int pos) const;//辅助函数,用来去获取节点指针,方便后续操作
public:
DblLinkList();//初始化咯
virtual ~DblLinkList();//析构
int Length() const;//这个地方也可以换成链表内变量length
bool Empty() const;//判空
void Clear();//清空表
void Treaverse();//遍历输出
bool GetElem(int pos, ElemType &e) const;//获取数据,判断是否存在的同时给一个接收值
bool SetElem(int pos, const ElemType &e);//设置数据(更好的理解是update?)
bool Delete(int position, ElemType &e);//删除数据
bool Insert(int position, const ElemType &e);//插入数据,某种程度来说是添加数据咯
DblLinkList(const DblLinkList<ElemType> &source);//拷贝构造函数
DblLinkList<ElemType> &operator=(const DblLinkList<ElemType> &source);//重载=
};
template<class ElemType>
DblNode<ElemType> *DblLinkList<ElemType>::GetElemPtr(int pos) const {
DblNode<ElemType> *temPtr = head;
int temPos = 0;
while (temPtr != nullptr && temPos <= pos) {
temPtr = temPtr->next;
temPos++;
}
if (temPtr != nullptr && temPos == pos + 1) {
return temPtr;
} else {
return nullptr;
}
}
template<class ElemType>
DblLinkList<ElemType>::DblLinkList() {//初始化,头尾相连
head = new DblNode<ElemType>;
tail = new DblNode<ElemType>;
head->next = tail;
tail->back = head;
}
template<class ElemType>
DblLinkList<ElemType>::~DblLinkList<ElemType>() {
Clear();
}
template<class ElemType>
int DblLinkList<ElemType>::Length() const {
int count = 0;
for (DblNode<ElemType> *temPtr = head->next; temPtr != tail; temPtr = temPtr->next) {
count++;
}
return count;
}
template<class ElemType>
bool DblLinkList<ElemType>::Empty() const {
return head->next == tail;//判空,头指向尾
}
template<class ElemType>
void DblLinkList<ElemType>::Clear() {
while (!Empty()) {
ElemType e;
Delete(0, e);
}
}
template<class ElemType>
void DblLinkList<ElemType>::Treaverse() {
DblNode<ElemType> *temPtr = this->head->next;
for (int i = Length();
i > 0; i--, temPtr = temPtr->next) {//这里不使用temPtr != nullptr是由于在tail->next才是nullptr,这导致多输出一个随机数据!
cout << temPtr->data << " ";
}
cout << endl;
}
template<class ElemType>
bool DblLinkList<ElemType>::GetElem(int pos, ElemType &e) const {
if (pos < 0 || pos > Length()) {//合理区间为:[0,length())
return false;
} else {
DblNode<ElemType> *temPtr = GetElemPtr(pos);
e = temPtr->data;
return true;
}
}
template<class ElemType>
bool DblLinkList<ElemType>::SetElem(int pos, const ElemType &e) {
if (pos < 0 || pos > Length()) {//合理区间为:[0,length())
return false;
} else {
DblNode<ElemType> *temPtr = GetElemPtr(pos);
temPtr->data = e;
return true;
}
}
template<class ElemType>
bool DblLinkList<ElemType>::Delete(int position, ElemType &e) {
if (position < 0 || position > Length()) {//合理区间为:[0,length())
return false;
} else {
DblNode<ElemType> *temp = GetElemPtr(position - 1);
DblNode<ElemType> *nextPtr = temp->next;
e = nextPtr->data;
temp->next = nextPtr->next;
nextPtr->next->back = temp;
delete nextPtr;
return true;
}
}
template<class ElemType>
bool DblLinkList<ElemType>::Insert(int position, const ElemType &e) {
if (position < 0 || position > Length()) {//合理区间为:[0,length())
return false;
} else {
DblNode<ElemType> *temp = GetElemPtr(position - 1);
DblNode<ElemType> *newPtr = new DblNode<ElemType>(e, temp, temp->next);
temp->next->back = newPtr;
temp->next = newPtr;
return true;
}
}
template<class ElemType>
DblLinkList<ElemType>::DblLinkList(const DblLinkList<ElemType> &source) {
this->head = new DblNode<ElemType>;
this->tail = new DblNode<ElemType>;
this->head->next = this->tail;
this->tail->back = this->head;
int length = source.Length();
for (int i = length - 1; i > -1; i--) {
ElemType e;
source.GetElem(i, e);
this->Insert(0, e);
}
}
template<class ElemType>
DblLinkList<ElemType> &DblLinkList<ElemType>::operator=(const DblLinkList<ElemType> &source) {
DblLinkList<ElemType> a = DblLinkList<ElemType>(source);
*this = a;
return *this;
}
int main() {
DblLinkList<int> a;
cout << "当前表长度:" << a.Length() << endl;
cout << "当前表是否为空:" << a.Empty() << endl;
for (int i = 0; i < 10; i++) {
a.Insert(0, i);
}
cout << "当前表长度:" << a.Length() << endl;
cout << "输出表如下:" << endl;
a.Treaverse();
DblLinkList<int> b = a;
DblLinkList<int> c(a);
cout << "测试operator=如下:" << endl;
b.Treaverse();
c.Treaverse();
return 0;
}
总结
-
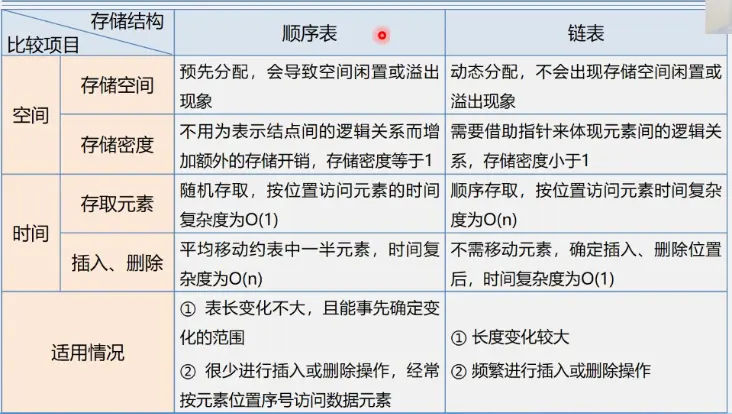
链式存储结构的优点
- 结点空间可以动态申请和释放
- 数据元素的逻辑次序靠结点的指针来指示,插入和删除时不需要移动数据元素
-
链式存储结构的缺点
- 存储密度(结点数据本身占用空间/结点占用的空间总量,即顺序存储结构存储密度为1)小,每个结点的指针域需要额外占用储存空间。当每个结点的数据域所占字节不多时,指针域所占用存储空间的比重显得很大。
- 链式存储结构为非随机存取结构。对任一结点的操作都要从头/尾指针依指针链查找该结点,这增加了算法的复杂度。由该缺点可以得出单向链表和循环链表相较于双向链表的差别:
- 单向链表和循环链表都只能从一个方向进行查找,这相较于双向链表很多时候是更慢的
- 双向链表在牺牲更多空间的同时获得了双向查找的能力,比及单向链表和循环链表有着更高的查找效率
栈和队列
定义
栈(stack):限定只在表头/表尾(仅一端)进行插入(入栈)与删除(出栈)操作的线性表,操作的这一端称为栈顶,另一端称为栈底。
队列(queue):限定在一端进行插入(入队)操作,另一端进行删除(出队)操作的线性表,入队一端称为队尾,出队一端称为队头。
特点
栈的操作具有后进先出(Last In First Out,LIFO) 的固有特性
队列的操作具有先进先出(First In First Out, FIFO) 的固有特性
这里有一个比较贴切的形容,栈可以当做弹夹,队列就是人排队咯。
结构
栈和队列都是顺序表的子集,结构上是类似于顺序表的,仅在插入与删除方面有特点,不作过多叙述。
代码部分
本质上还是线性表,既有顺序存储结构也有链式存储结构,仅在插入与删除函数部分的实现有区别,但顺序存储和链式存储在时间效率上差异不大(操作位置是限定的),而存储结构是空间利用率是不够的,因此链式结构看看就行,主要掌握的是顺序结构哈。
这里就给出栈的顺序表实现
顺序栈的一种java实现
interface IStack {
//置空
public void clear();
//判空
public boolean isEmpty();
//返回栈中元素个数
public int length();
//读取栈顶元素
public Object peek();
//入栈
public void push(Object o) throws Exception;
//返回栈顶元素 出栈
public Object pop();
}
class SqStack implements IStack{
//对象数组实现栈
private Object[] stackElem;
//指向下一存储位置 为0时表示为空
private int top = 0;
public SqStack(int maxSize) {
stackElem = new Object[maxSize];
}
@Override
public void clear() {
top = 0;
}
@Override
public boolean isEmpty() {
return top == 0;
}
@Override
public int length() {
//top指向下一存储位置 即指向的是当前 下标+1 = 当前表长
return top;
}
//读取栈顶元素
@Override
public Object peek() {
if(top != 0)
return stackElem[top - 1];
else
return null;
}
//入栈
@Override
public void push(Object o) throws Exception {
if(top == stackElem.length)
throw new Exception("栈已满。");
else
stackElem[top++] = o;
}
//出栈
@Override
public Object pop() {
if(isEmpty())
return null;
else {
top = top - 1;
return stackElem[top];
}
}
}
public class StackDemo {
public static void main(String[] args) throws Exception {
SqStack sqStack = new SqStack(5);
sqStack.push("零");
sqStack.push("一");
sqStack.push("二");
sqStack.push("三");
System.out.println("==========================");
System.out.println("peek()测试,返回栈顶元素");
System.out.println("栈顶元素为: " + sqStack.peek());
System.out.println("==========================");
System.out.println("出栈测试,返回栈顶元素");
System.out.println("pop()出栈元素为: " + sqStack.pop() + " 出栈后栈顶元素为:" + sqStack.peek());
System.out.println("==========================");
System.out.println("入栈测试,返回栈顶元素");
sqStack.push("三");
System.out.println("入栈后栈顶元素为: " + sqStack.peek());
System.out.println("==========================");
System.out.println("length()测试,返回栈顶元素");
System.out.println("当前栈长度为: " + sqStack.length());
System.out.println("==========================");
System.out.println("栈满测试,存入元素四。");
sqStack.push("四");
System.out.println("当前栈顶元素为: " + sqStack.peek() + " 栈的长度为: " + sqStack.length());
System.out.println("尝试往已满栈中放入元素。");
try {
sqStack.push("五");
}
catch (Exception e){
System.out.println(e.toString());
}
System.out.println("==========================");
System.out.println("判空测试");
if(!sqStack.isEmpty()) {
System.out.println("栈不为空。栈顶元素为:" + sqStack.peek());
}
System.out.println("置空测试.");
sqStack.clear();
if(sqStack.isEmpty()) {
System.out.println("栈为空。栈顶元素为:" + sqStack.peek());
System.out.println("入栈元素wu." );
sqStack.push("wu");
System.out.println("栈顶元素为:" + sqStack.peek());
}
}
}
链栈的一种C++实现
#include <iostream>
using namespace std;
template<class T> class LinkStack;
template<class T>
class Node {
public:
friend class LinkStack<T>;
private:
explicit Node(const T& data, Node* n = nullptr)
:data(data), link(n) {};
private:
T data;
Node<T>* link;
};
template<class T>
class LinkStack {
private:
Node<T>* top;
public:
LinkStack()
:top(0) {};
~LinkStack() { deleteStack(); }
public:
T& getTop()const;
void push(const T& e);
void pop();
bool isEmpty()const;
void deleteStack();
};
/* 判空 */
template<class T>
bool LinkStack<T>::isEmpty() const {
return top == 0;
}
/* 入栈 */
template<class T>
void LinkStack<T>::push(const T& e) {
top = new Node<T>(e, top);
}
/* 查看栈顶元素 */
template<class T>
T& LinkStack<T>::getTop() const
{
if (this->isEmpty())
throw "Stack is empty";
return top->data;
}
/* 出栈 */
template<class T>
void LinkStack<T>::pop() {
if (this->isEmpty())
throw "Stack is empty. Cannot delete.";
Node<T>* delNode = top;
top = top->link;
delete delNode;
}
template<class T>
void LinkStack<T>::deleteStack() {
while (!isEmpty())
pop();
}
int main()
{
cout << "test" << endl;
LinkStack<int> s;
s.push(10);
cout << s.getTop() << endl;
s.push(20);
s.push(30);
cout << s.getTop() << endl;
s.pop();
cout << s.getTop() << endl;
return 0;
}
顺序队列的一种C++实现
#include <iostream>
#include <string>
using namespace std;
template <typename T>
class arrayQueue
{
private:
int front; //头元素下标
int rear; //尾元素下标
int maxSize; //队列总空间大小
T* array;
public:
arrayQueue(int size = 10) //构造函数
{
front = 1;
rear = 0;
maxSize = size + 1;
array = new T[maxSize];
}
T back()
{
if (empty())
{
cout << "队列为空" << endl;
return NULL;
}
return array[rear];
}
bool empty()
{
if (size() == 0)
return true;
return false;
}
T frontValue()
{
if (empty())
{
cout << "队列为空" << endl;
return NULL;
}
else
{
return array[front];
}
}
void pop()
{
if (empty())
cout << "队列已经为空" << endl;
else
front = (front + 1) % maxSize;
}
void push(T value)
{
if (size() == maxSize - 1)
{
cout << "队列已满,无法继续添加元素" << endl;
}
else
{
rear = (rear + 1) % maxSize;
array[rear] = value;
}
}
int size()
{
return (rear + maxSize - front + 1) % maxSize;
}
};
int main()
{
arrayQueue<string> q(6);
q.push("abc");
q.push("def");
q.push("ghi");
q.push("jkl");
q.push("mno");
q.push("pqr");
int len = q.size();
cout << q.back() << endl;
for (int i = 0; i < len; i++)
{
cout << q.frontValue() << endl;
q.pop();
}
cout << q.empty() << endl;
return 0;
}
链队列的一种C++实现
#include <iostream>
#include <string>
using namespace std;
template <typename T>
class Node
{
public:
T value;
Node *next;
Node(T value, Node* next = NULL)
{
this->value = value;
this->next = next;
}
};
template <typename T>
class Myqueue
{
private:
Node<T> *front;
Node<T> *rear;
int length;
public:
Myqueue()
{
front = rear = NULL;
length = 0;
}
T back()
{
if (empty())
{
cout << "队列为空" << endl;
return NULL;
}
return rear->value;
}
bool empty()
{
if (size() == 0)
return true;
return false;
}
T frontValue()
{
if (empty())
{
cout << "队列为空" << endl;
return NULL;
}
else
return front->value;
}
void pop()
{
if (empty())
cout << "队列已经为空" << endl;
else
{
Node<T> *temp = front;
front = front->next;
if (rear == temp)
rear = front;
delete (temp);
length--;
}
}
void push(T value)
{
length++;
if (length == 1)
{
front = new Node<T>(value, NULL);
rear = front;
}
else
{
rear->next = new Node<T>(value, NULL);
rear = rear->next;
}
}
int size()
{
return length;
}
};
int main()
{
Myqueue<string> q;
q.push("abc");
q.push("def");
q.push("ghi");
q.push("jkl");
q.push("mno");
q.push("pqr");
int len = q.size();
cout<<len<<endl;
cout << q.back() << endl;
for (int i = 0; i < len; i++)
{
cout << q.frontValue() << endl;
q.pop();
}
cout << q.empty() << endl;
return 0;
}
总结
栈:
-
定义:限定只能在表的一端进行插入和删除操作运算的线性表(只能在栈顶操作)
-
逻辑结构:同线性表一样栈元素具有线性关系即前驱后继关系(一对一)
-
存储结构:顺序栈和链栈均可,顺序栈更常见
-
运算规则:只能在栈顶运算,且访问结点时依照后进后出的原则(LIFO)
-
实现方式:关键是编写入栈和出栈函数具体实现依顺序栈和链栈的不同而不同
栈和线性表唯一的区别在于运算规则。线性表插入删除位置任意,而栈只能对表尾(栈顶)的元素进行插入和删除操作(后进先出的原则)
队列:
-
定义:只能在表的一端进行插入运算在表的另一端进行删除操作运算的线性表(头删尾插)
-
逻辑结构:同线性表一样栈元素具有线性关系即前驱后继关系(一对一)
-
存储结构:顺序队和链队均可,循环顺序队更常见
-
运算规则:只能在队首和队尾运算,且访问结点时依照后进先出的原则(FIFO)
-
实现方式:关键是掌握入队和出队操作具体实现依顺序队和链队的不同而不同
串
定义
串(String)是由零个或多个任意字符组成的有限序列又名字符串
(用双引号括起来有些书中也用单引号)所谓序列说明串的相邻字符之间具有前驱和后继关系
特点
内容受限制的线性表,内容只能是字符
结构
可参考线性表(顺序串、链串)
代码部分
顺序实现如下(C++):
#include <iostream>
/*以下是String类,实现了它的默认、拷贝构造函数(用“=”重载完成,重载了两种参数的:字符数组和String类型),
同时也只是重载了“[]”和“<<”运算符*/
class String
{
private:
char* m_Buffer;
unsigned int m_Size;
public:
String()
{
m_Size = 4;
m_Buffer = new char[m_Size + 1];
memcpy(m_Buffer, "C++!", 5);
}
String(const char* string)
{
*this = string;
/*m_Size = strlen(string);
m_Buffer = new char[m_Size + 1];
memcpy(m_Buffer, string, m_Size + 1);*/
//m_Buffer[m_Size] = 0;
}
String(const String& other)
/*:m_Size(other.m_Size)*/
{
/*std::cout << other.m_Buffer << "Copied String!" << std::endl;
m_Buffer = new char[m_Size + 1];
memcpy(m_Buffer, other.m_Buffer, m_Size + 1);*/
*this = other;
}
~String()
{
delete[]m_Buffer;
}
char& operator[](unsigned int index);
String& operator =(const String& other);
String& operator =(const char* string);
friend std::ostream& operator <<(std::ostream& stream, const String& string);
};
String& String::operator =(const String& other)
{
/*std::cout << other.m_Buffer << "Copied String!" << std::endl;*/
m_Size = other.m_Size;
m_Buffer = new char[m_Size + 1];
memcpy(m_Buffer, other.m_Buffer, m_Size + 1);
return *this;
}
String& String::operator =(const char* string)
{
m_Size = strlen(string);
m_Buffer = new char[m_Size + 1];
memcpy(m_Buffer, string, m_Size + 1);
return *this;
}
std::ostream& operator <<(std::ostream& stream, const String& string)
{
stream << string.m_Buffer;
return stream;
}
char& String::operator[](unsigned int index)
{
return m_Buffer[index];
}
//重要的是PrintString方法,后续用来在Human类及其子类去打印数据
void PrintString(const String& string)
{
std::cout << string << std::endl;
}
int main(void) {
String str = String("Hello World!");
PrintString(str);
return 0;
}
总结
需要注意有关结构的基本操作:
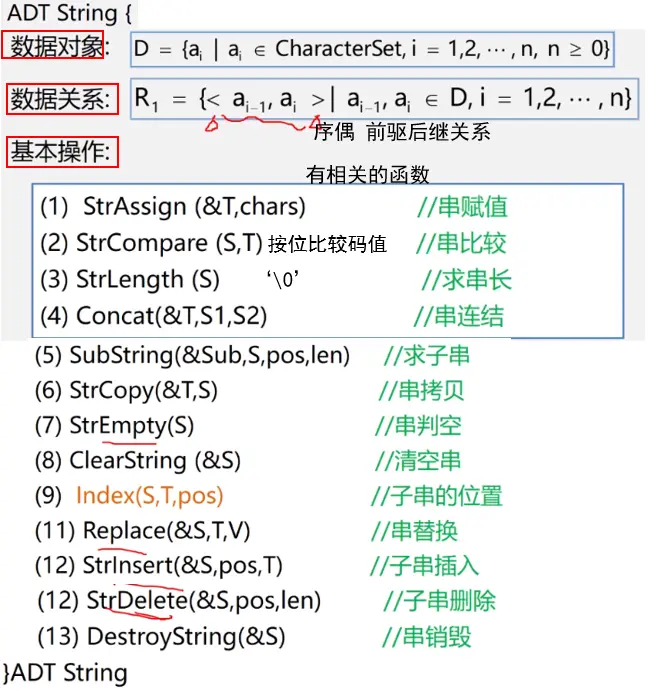
重点关注子串查找的BF算法和KMP算法**
BF算法(Brute-Force,又称古典的、经典的、朴素的、穷举的)
一种采用穷举的暴力算法
演示如下:
注意回溯时是 i - j + 2 或 i - (j - 1) + 1
KMP算法,一种更高效的查找算法(可达到O(n+m))
首先本算法中指向文本串的指针不回退
其次需要弄清楚前缀表(next表)的生成即使用方法
举例如下:
文本串“aabaabaaf”
模式串“aabaaf”
模式串对应next表为:010120计算方法为:最长相等的前后缀(前缀为包含首字母不包含尾字母的全部子串,后缀为包含尾字母不包含首字母的全部子串)
过程如下:
a即第一个字母,没有前后缀,默认为0
aa即最长相等前后缀为1
aab依先前规则,显然为0
aaba易知为1
aabaa为2
aabaaf无相等前后缀,为0使用方法如下:
aabaabaafaabaaf
010120此时文本串指针指至5(第二个b),出现不匹配,在模式串指针中指向f,其前一位a对应next表值为2,即此时文本指针继续查找5(第二个b),不过模式串指针从第一位开始,但前进2位,即回退至2处(第一个b),继续完成匹配,发现匹配成功。
这里需要注意的是,依据next表值作回退前进位时,位数为0或1都需要前进一位(思考一下)以上KMP算法部分可参考视频 帮你把KMP算法学个通透!(理论篇)
最浅显易懂的 KMP 算法讲解
给出一种java的实现如下:package com.drizzledrop.test; import java.util.Arrays; public class KMPAlgorithm { public static void main(String[] args) { String str1 = "BBC ABCDAB ABCDABCDABDE"; String str2 = "ABCDABD"; //String str2 = "BBC"; int[] next = kmpNext("ABCDABD"); //[0, 1, 2, 0] System.out.println("next=" + Arrays.toString(next)); int index = kmpSearch(str1, str2, next); System.out.println("index=" + index); // 15 了 } /** * @param str1 源字符串 * @param str2 子串 * @param next 部分匹配表, 是子串对应的部分匹配表 * @return 如果是-1 就是没有匹配到,否则返回第一个匹配的位置 */ public static int kmpSearch(String str1, String str2, int[] next) { //遍历 for (int i = 0, j = 0; i < str1.length(); i++) { //需要处理 str1.charAt(i) != str2.charAt(j), 去调整 j 的大小 //KMP 算法核心点, 可以验证... while (j > 0 && str1.charAt(i) != str2.charAt(j)) { j = next[j - 1]; } if (str1.charAt(i) == str2.charAt(j)) { j++; } if (j == str2.length()) {//找到了 // j = 3 i return i - j + 1; } } return -1; } //获取到一个字符串(子串) 的部分匹配值表 public static int[] kmpNext(String dest) { //创建一个 next 数组保存部分匹配值 int[] next = new int[dest.length()]; next[0] = 0; //如果字符串是长度为 1 部分匹配值就是 0 for (int i = 1, j = 0; i < dest.length(); i++) { //当 dest.charAt(i) != dest.charAt(j) ,我们需要从 next[j-1]获取新的 j //直到我们发现 有 dest.charAt(i) == dest.charAt(j)成立才退出 //这是 kmp 算法的核心点 while (j > 0 && dest.charAt(i) != dest.charAt(j)) { j = next[j - 1]; } //当 dest.charAt(i) == dest.charAt(j) 满足时,部分匹配值就是+1 if (dest.charAt(i) == dest.charAt(j)) { j++; } next[i] = j; } return next; } }
数组
定义
按一定格式排列起来的,具有相同类型的数据元素的集合。(在python中,列表和数组最大的区别就在于列表可以储存不同类型的数据元素;而在java中,列表和数组最大的区别在于数组(Array)大小是固定的,列表(ArrayList)大小是能动态变化的)
数组在不同语言中是有些许差别的,一般不做特别要求(即常识了解,用时再查)。
特点
java:
- 其长度是确定的。数组一旦被被创建,它的大小就是不可以改变的。
- 其元素必须是相同类型,不允许出现混合类型。
- 数组中的元素可以是任何数据类型,包括基本类型和引用类型
- 数组变量属引用类型,数组也可以看成是对象,数组中的每个元素相当于该对象的成员变量。
c/c++:
- 数组是一种变量的集合,在这个集合中,所有变量的数据类型都是相同的;
- 每一个数组元素的作用相当于简单变量;
- 同一数组中的数组元素在内存中占据的内存空间是连续的;
- 数组的大小(数组元素的个数)必须在定义时确定,在程序中不可改变;
- 数组名代表的是数组在内存中的首地址。
结构
一维数组常见为线性结构,定长的线性表。
二维数组有非线性结构(每一个数据元素既在一个行表中,又在一个列表中),也有线性结构(即定长的线性表,而改线性表的每个数据元素也是一个定长的线性表)
......
n维数组
代码部分
略
总结
线性表结构可以理解成数组结构的一个特例,而数组结构又是线性表结构的扩展。
一般对数组的操作,除了结构的初始化和销毁之外,只有取元素和修改元素值的操作。
常见的矩阵(特殊矩阵、三角矩阵、稀疏矩阵等)的实现都可以通过数组来实现
广义表
定义
广义表又称列表(List),是n>=0个元素的有限序列,其中每一个元素可以是单个数据元素(称为原子元素,简称原子),也可以是满足本定义的广义表(称为子表元素,或简称为子表)。一个很好的例子是python中的list数据类型。
特点
- 广义表中的数据元素有相对次序;
- 广义表的长度定义为最外层包含元素个数;
- 广义表的深度定义为所含括弧的重数。其中原子的深度为0,空表的深度为1;
- 广义表可以共享;一个广义表可以为其他广义表共享;这种共享广义表称为再入表;
- 广义表可以是一个递归的表。一个广义表可以是自已的子表。这种广义表称为递归表。递归表的深度是无穷值,长度是有限值;
- 任何一个非空广义表GL均可分解为表头head(GL) = a1和表尾tail(GL) = ( a2,…,an) 两部分。
结构
广义表是一种递归的数据结构,因此很难为每个广义表分配固定大小的存储空间,所以其存储结构只好采用动态链接结构。
一般不做要求,自主探索见:广义表
代码部分
略
总结
关于表头和表尾区别:
广义表((a,b),c,d)表头和表尾分别是什么?
- 表头:当广义表LS非空时,称第一个元素为LS的表头;
- 表尾:称广义表LS中除去表头后其余元素组成的广义表为LS的表尾。
表头是元素,表尾是广义表。
举个几个例子
广义表(a, (b))的表头是单元素a,表尾是广义表((b))。在(b)的外面加一层小括号,才能变成广义表。因此是((b))。
广义表(a)的表头是单元素a,表尾是广义表(),a后面没有元素了,想想表尾一定是个广义表。就是一定带()。
广义表(a, b, c)的表头是单元素a,表尾是广义表(b,c)。
大体上的总结:
- 对任意一个非空的广义表,其表头可能是单元素,也可能是广义表,
- 而其表尾一定是广义表。
- 注意表尾的深度(即括号的嵌套层数)
- 表尾是由除了表头以外的其余元素组成的广义表,所以,需要在表尾的直接元素外面再加一层括号。
树
树的定义
树(Tree)是n (n≥0)个结点的有限集(显然,树的定义是一个递归的定义)。若n = 0,称为空树;若n >0,则它满足如下两个条件:
- 有且仅有一个特定的称为根(Root)的结点;
- 其余结点可分为m (m≥0)个互不相交的有限集T1,T2,T3,....Tm,其中每一个集合本身又是一棵树,并称为根的子树(SubTree)。
结点与度
结点:树中的每个元素分别对应一个结点,结点包含数据元素值及其逻辑关系信息(一个数据元素以及若干指向其子树的分支)。
结点的度:结点拥有子树的数目(一代几子)。
树的度:树内结点的最大值(一代最多子)。
叶子/终端结点:度为0的结点。
分支/非终端结点:除叶子结点外,其他结点。
内部结点:除根结点外,其他全部分支结点(即不含根结点和终端结点)。
结点层次:结点的层次从根开始定义起,根结点层次为1,向下递增(多少代?)
树的深度:树中叶结点所在的最大层次(某一脉最多代?)

结点间关系
双亲和孩子:结点的子树的根称为该结点的孩子,相应的,该结点称为孩子的双亲,如下图中C的双亲为A,C的孩子有E、F和G。
兄弟:同一个双亲的孩子之间称为兄弟,如下图中的E、F和G。
祖先:从根到该结点所经历的分支上的所有结点,如下图中的J的祖先为A、C、E。
子孙:以某点为根的子树中的任一结点都称为该结点的子孙。如下图中的B的子孙有D、H、I。
堂兄弟:双亲在同一层的结点互为堂兄弟,如下图中的D、E。
如果将树中结点的各子树堪称从左至右是有次序的,不能互换的,则称该树为有序树,否则为无序树。

二叉树
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两个互不相交的、分别称为根结点左子树和右子树的二叉树组成。
如下图中,图一是一个正确的二叉树,图二则不是二叉树,因为C结点有3个孩子。

二叉树的特点
- 每个结点最多有两个子树,所以二叉树中不存在度大于2的结点。
- 左子树和右子树是有顺序的,次序不能颠倒。
- 即使树中只有一颗子树,也要区分是左子树还是右子树。
二叉树的五种形态:
- 空二叉树。
- 只有一个根结点。
- 根结点只有左子树。
- 根结点只有右子树。
- 根结点既有左子树,又有右子树。
如果二叉树不为空,且有3个结点,那么其形态如下图:

特殊二叉树
斜树
斜树一定是斜的,所有的结点都只有左子树叫做左斜树,所有的结点都只有右子树叫做右斜树,左斜树和右斜树统称为斜树。
上图中树2和树3就是斜树。
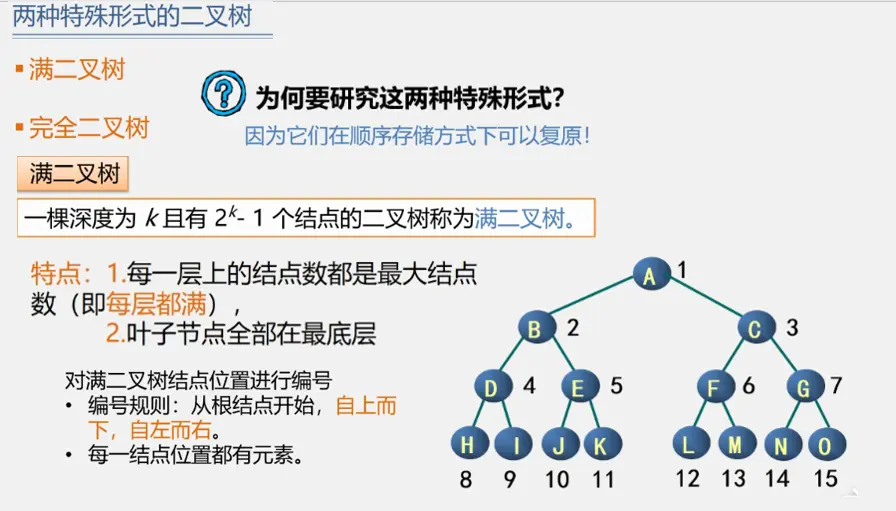
满二叉树
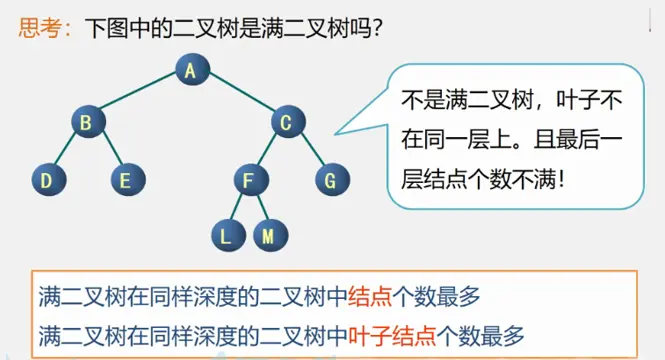
在一棵二叉树中,所有的分支结点都有左子树和右子树,并且所有的叶子结点都在同一层上,这样的二叉树称为满二叉树。如下图所示:

满二叉树有特点:
- 叶子结点只能出现在最下一层,出现在其他层就不能达到平衡,也就不是满二叉树了。
- 非叶子结点的度一定是2,如果有不是2的,那么此树就不是二叉树了。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子结点最多。
完全二叉树
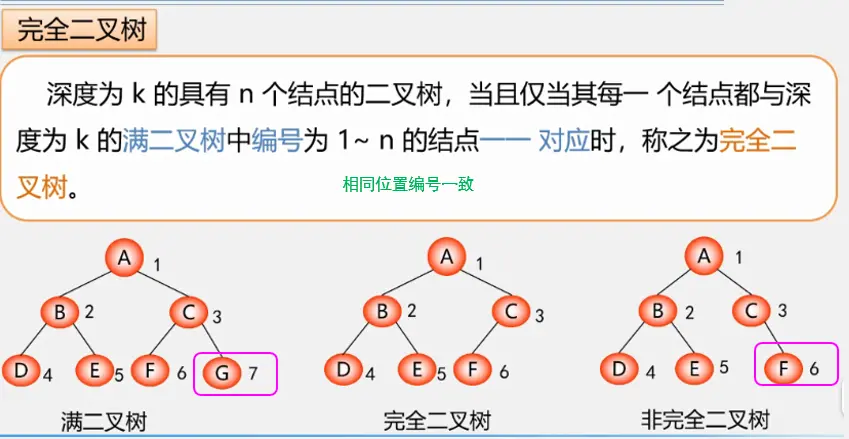
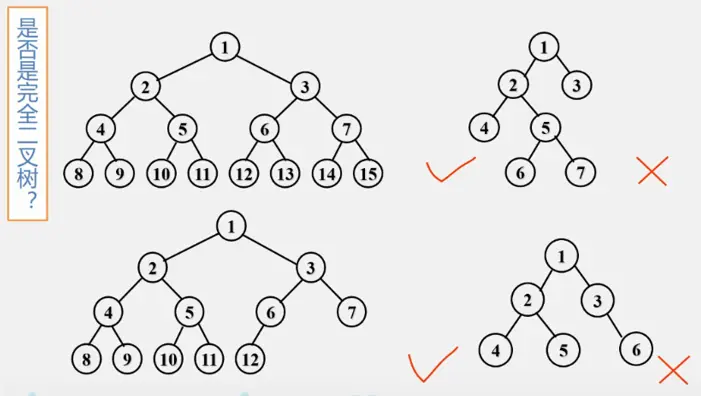
对于一棵具有n个结点的二叉树按照层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵树称为完全二叉树。如下图所示:

上图中:
- 如果没有结点6、结点7,而结点8、结点9仍存在,即结点3无孩子,那么这棵树就不是完全二叉树。
- 如果没有结点8,而结点9仍存在,即结点4只有右孩子,那么这棵树就不是完全二叉树。
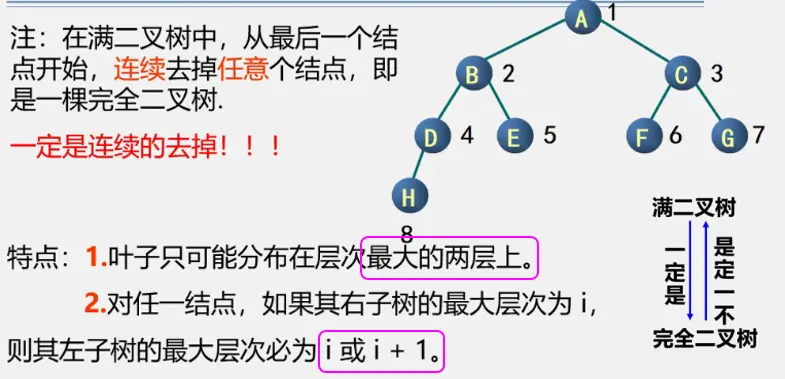
完全二叉树特点:
- 叶子结点只能出现在最下两层。
- 最下一层的叶子结点一定集中在左侧连续位置。
- 倒数第二层,如果有叶子结点,一定都集中在右侧连续位置。
- 如果结点度为1,那么只能有左孩子。
- 同样结点数的二叉树,完全二叉树的深度最小。
线索二叉树
遍历二叉树的其实就是以一定规则将二叉树中的结点排列成一个线性序列,得到二叉树中结点的先序序列、中序序列或后序序列。这些线性序列中的每一个元素都有且仅有一个前驱结点和后继结点。
但是当我们希望得到二叉树中某一个结点的前驱或者后继结点时,普通的二叉树是无法直接得到的,只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次,非常不方便。
于是是否能够改变原有的结构,将结点的前驱和后继的信息存储进来。
如果只是在原二叉树的基础上利用空结点,那么就存在着这么一个问题:我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点?rchild是指向右孩子还是后继结点?显然我们要对他的指向增设标志来加以区分。
因此,我们在每一个结点都增设两个标志域LTag和RTag,它们只存放0或1的布尔型变量,占用的空间很小。
LTag为0是指向该结点的左孩子,为1时指向该结点的前驱
RTag为0是指向该结点的右孩子,为1时指向该结点的后继
线索化
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
线索化具体实现
以中序二叉树的线索化为例,线索化的具体实现就是将中序二叉树的遍历进行修改,把原本打印函数的代码改为指针修改的代码就可以了。
我们设置一个pre指针,永远指向遍历当前结点的前一个结点。若遍历的当前结点左指针域为空,也就是无左孩子,则把左孩子的指针指向pre(相对当前结点的前驱结点)。
右孩子同样的,当pre的右孩子为空,则把pre右孩子的指针指向当前结点(相对pre结点为后继结点)。
最后把当前结点赋给pre,完成后续的递归遍历线索化。
中序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
//--------------------中间为修改空指针代码---------------------
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
//---------------------------------------------------------
InThreading(B->rchild,pre);
}
更详细内容可以参考 线索二叉树(详解)
二叉排序树
见动态搜索部分
二叉平衡树
见动态搜索部分
二叉树性质
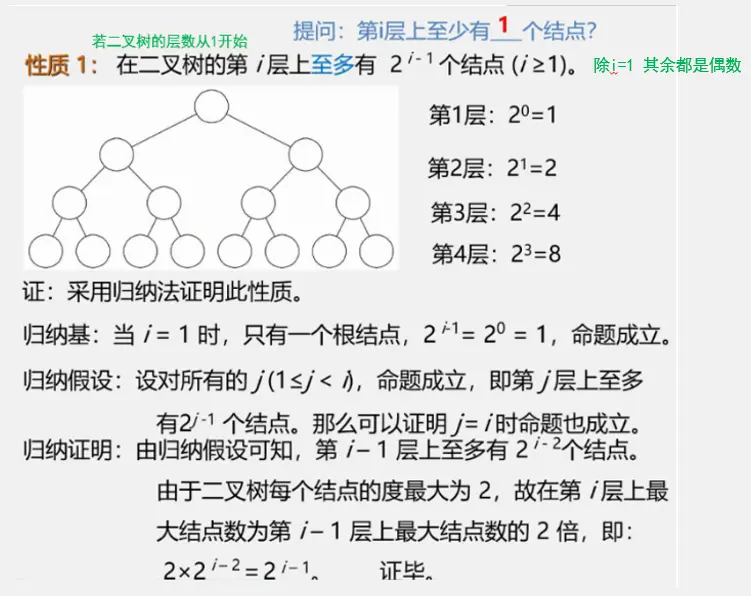

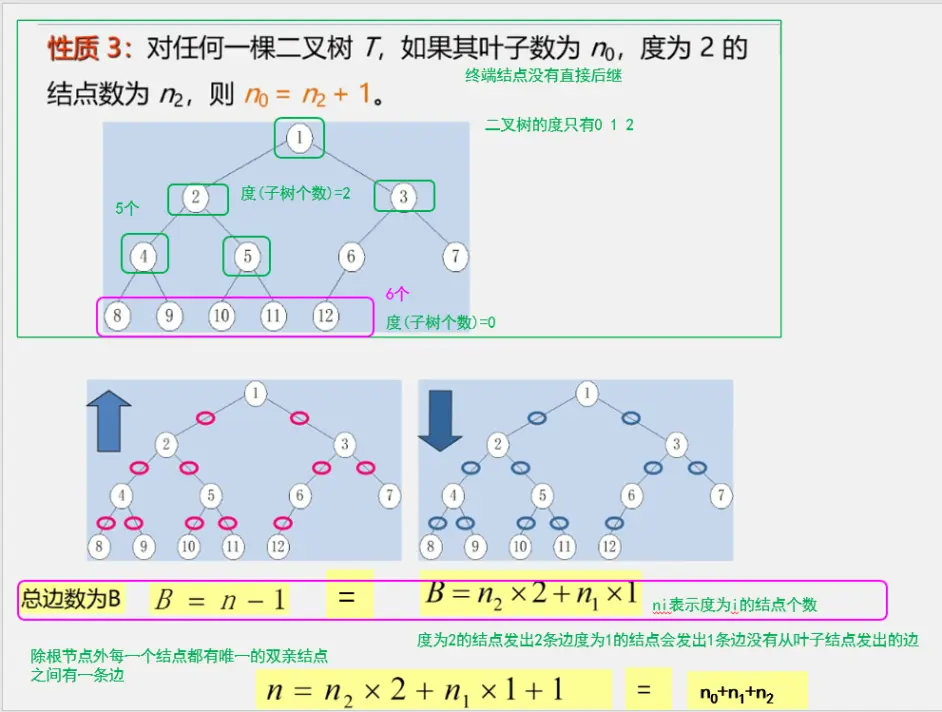
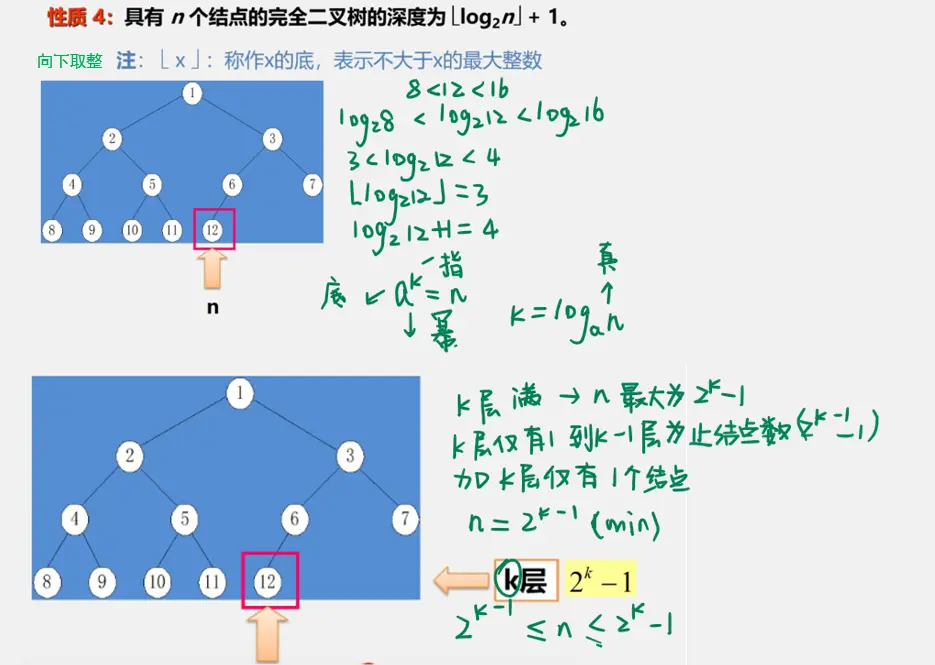

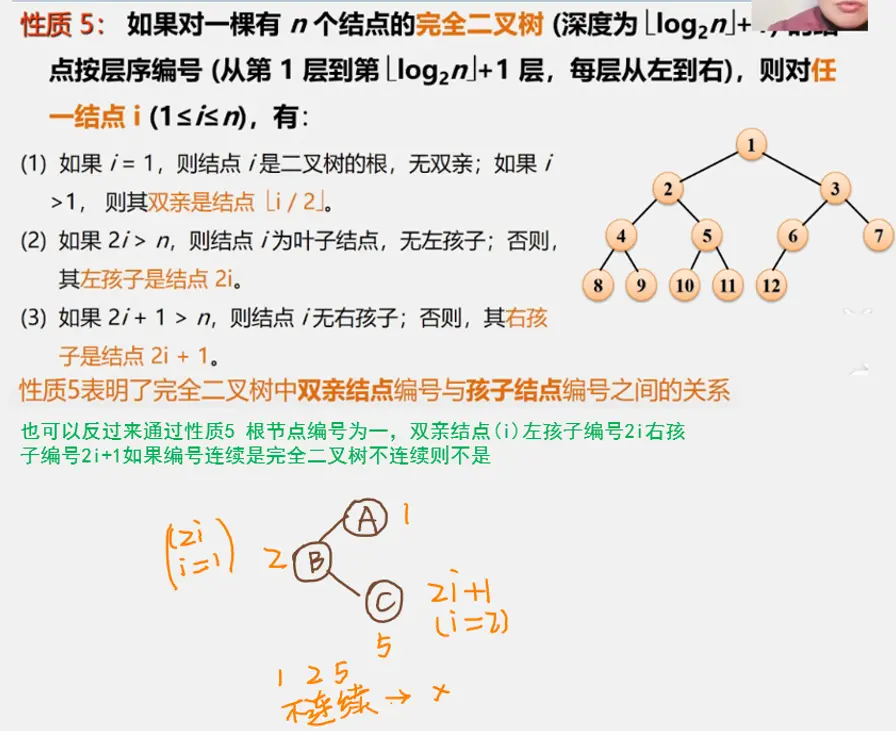
二叉树的储存结构
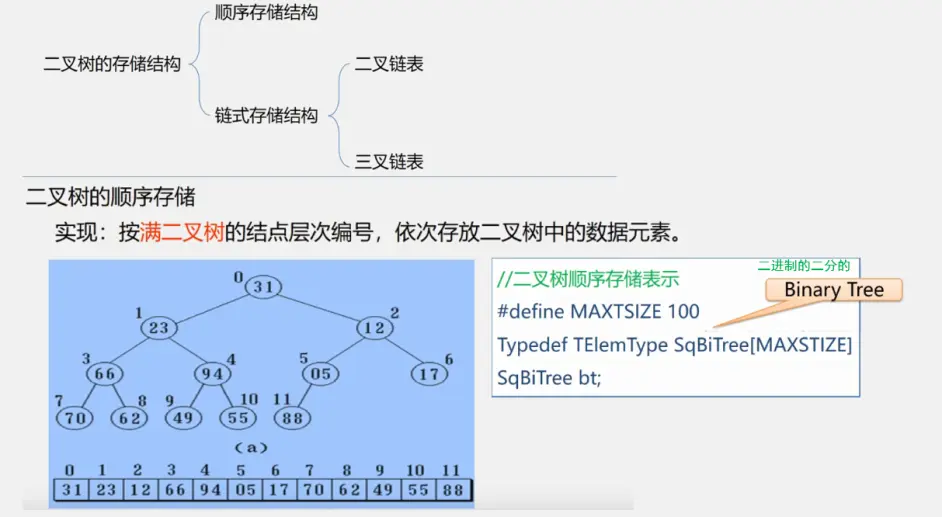
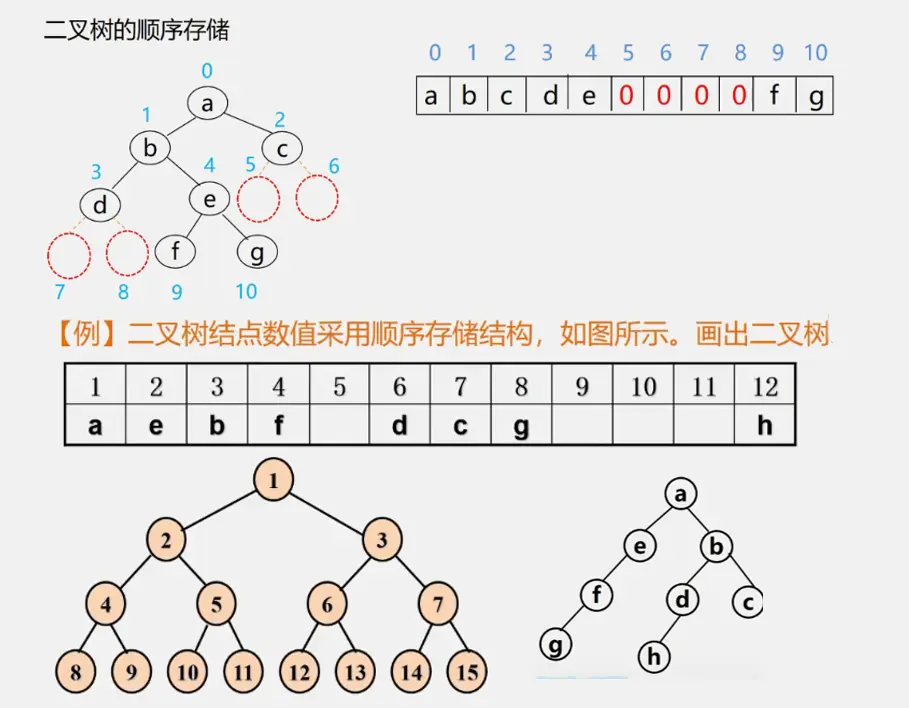
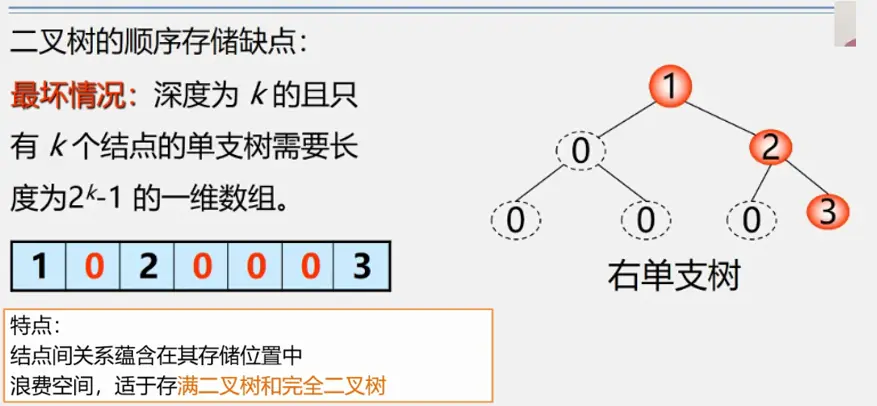
二叉树顺序存储的缺点:
顺序结构大小固定当树的元素个数变化比较大时,顺序存储不合适
一般情况我们说数组不需要存储地址,存储密度达到1很大 但对于树而言顺序结构通过编号来表示双亲和孩子/直接前驱后继的关系。当出现空结点时对应编号储存0或者不储存元素。这些位置就都被浪费掉了
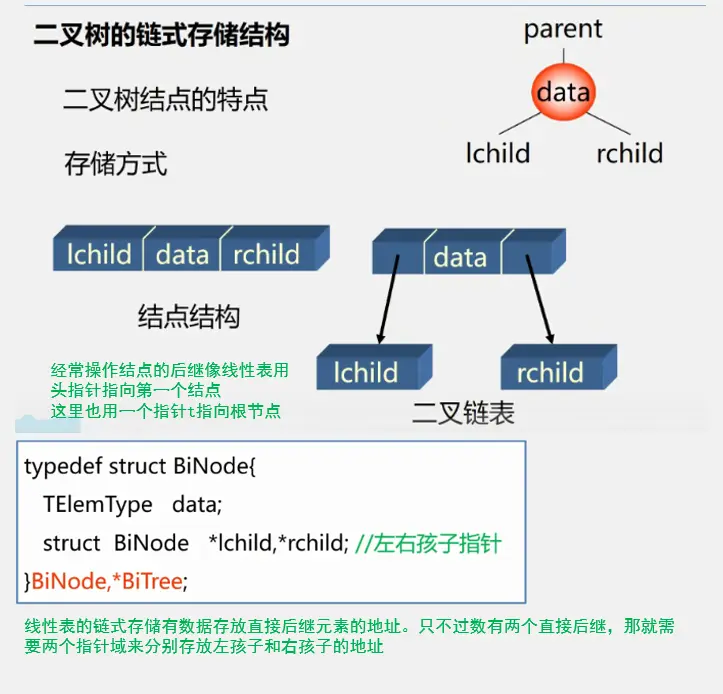
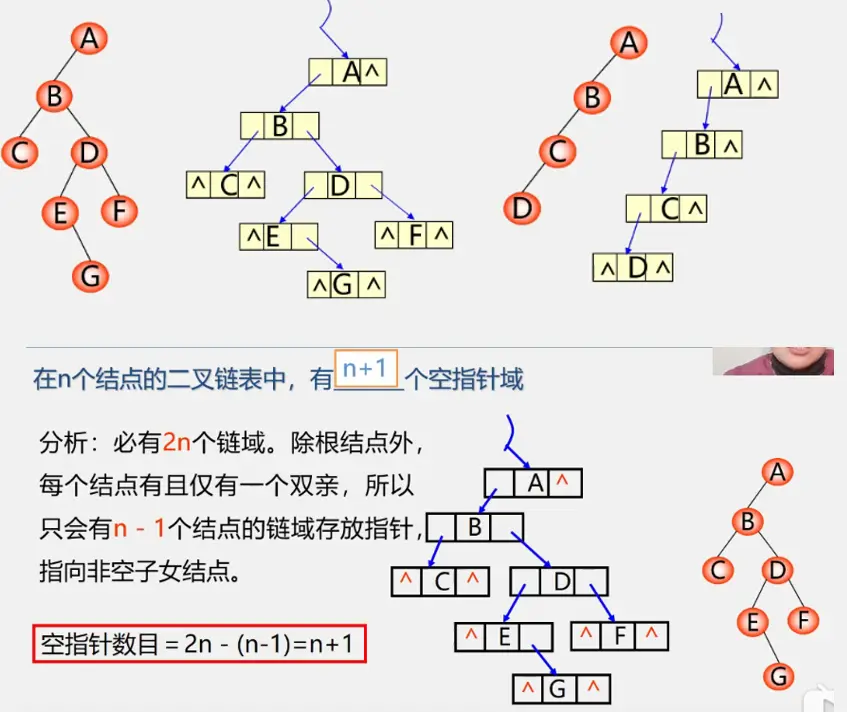
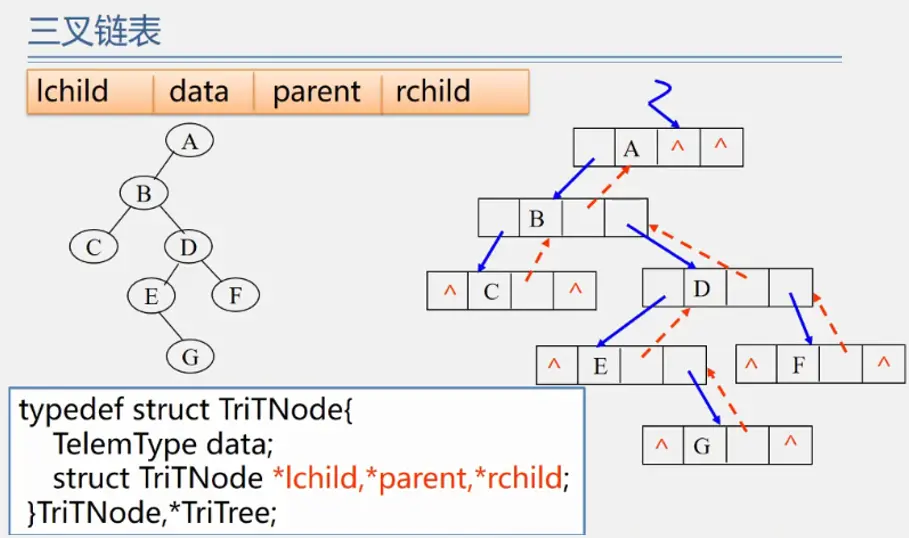
二叉树的遍历

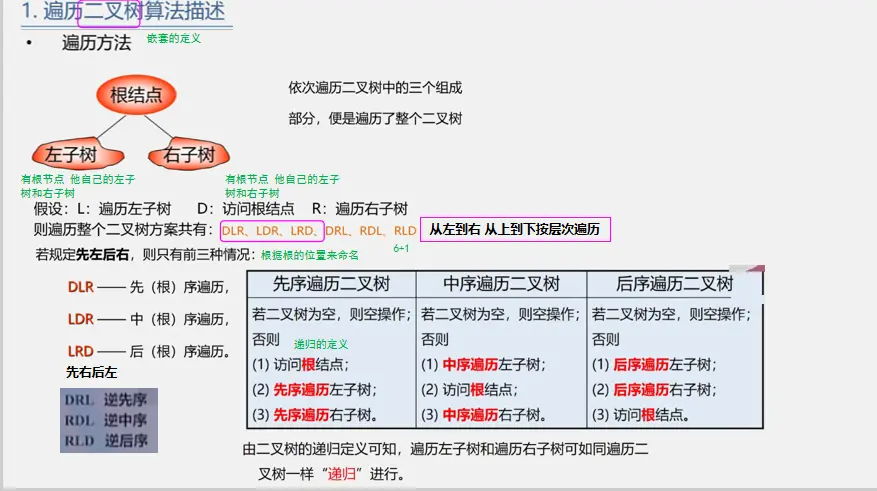
先序遍历
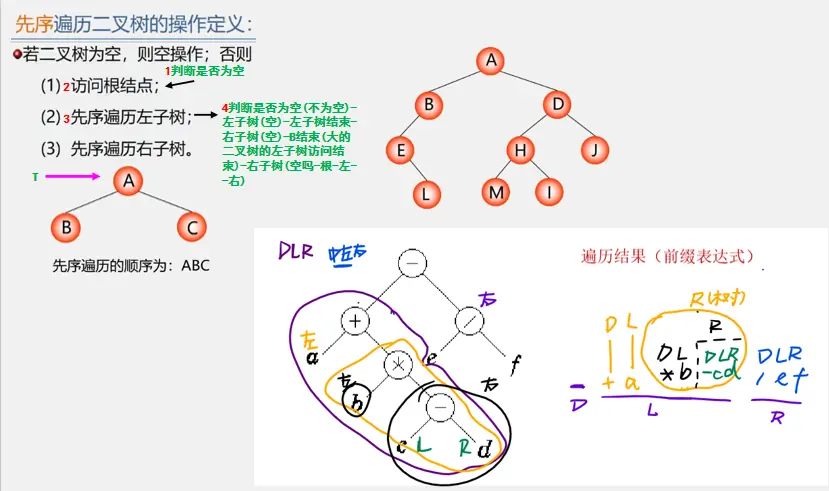
中序遍历
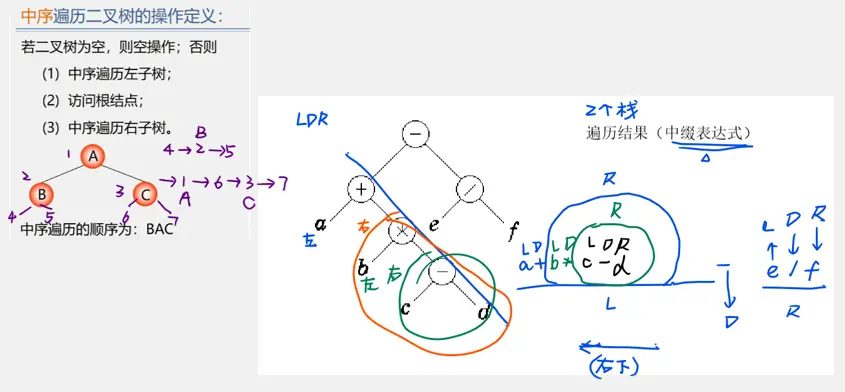
后序遍历
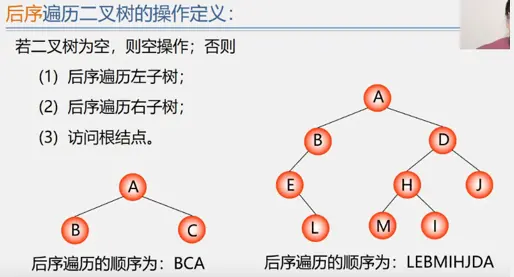
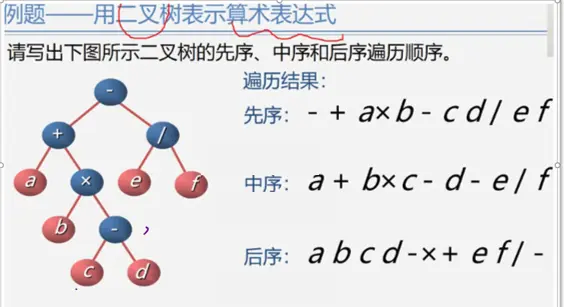
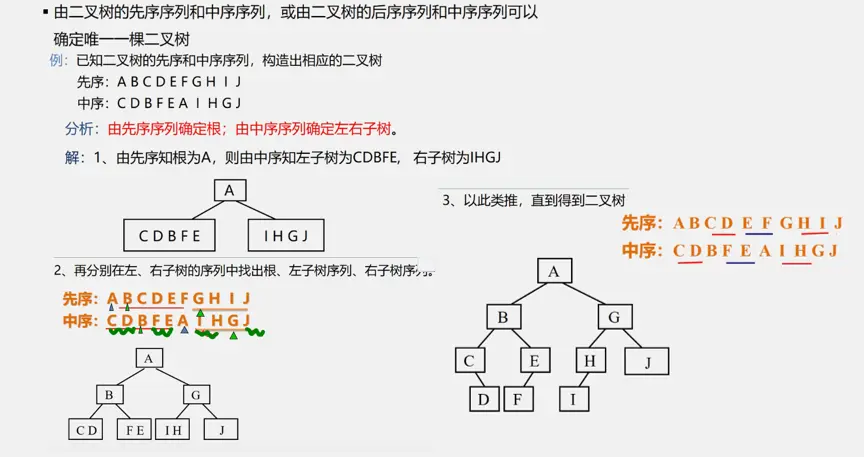
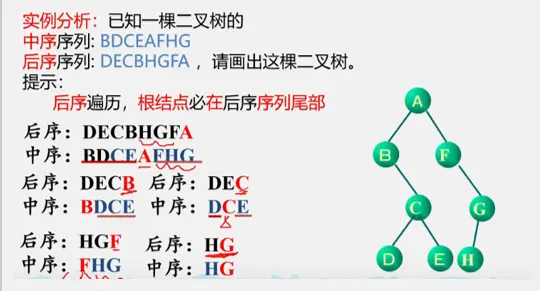
树和森林
定义
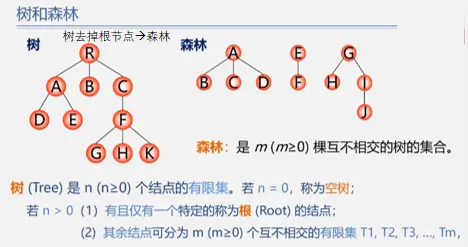
树与二叉树的相互转换
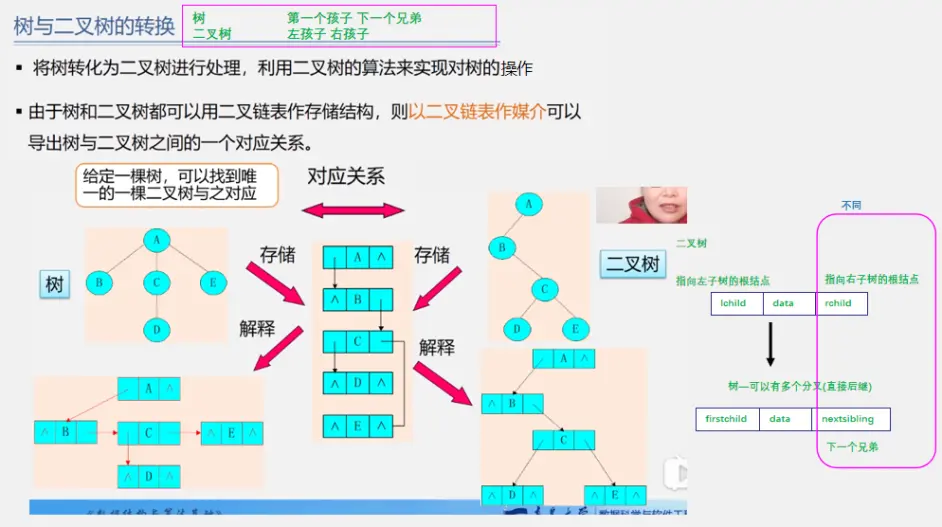
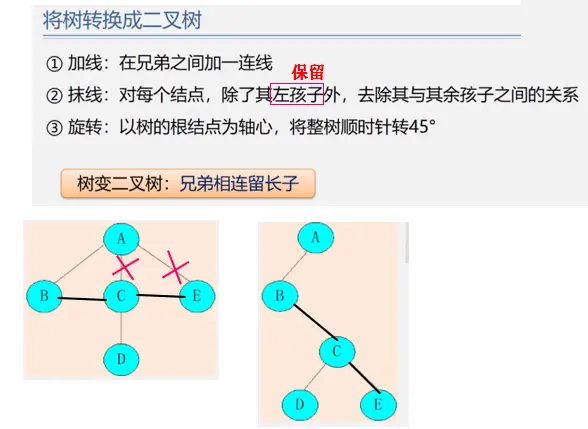
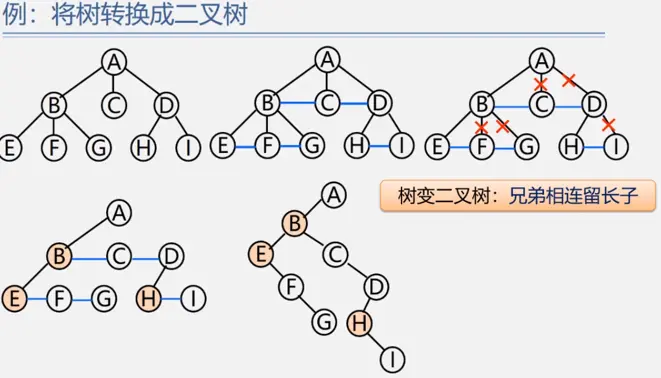
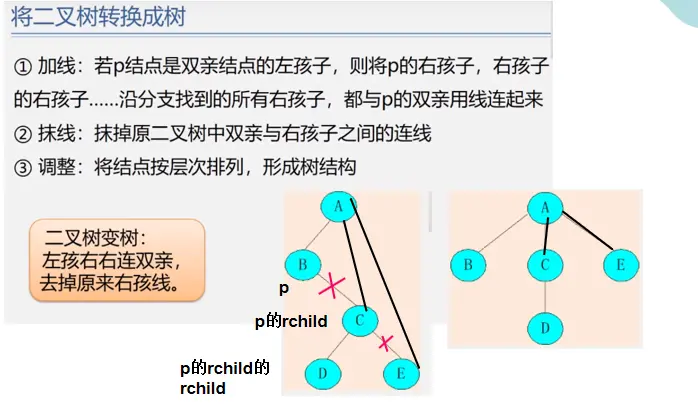
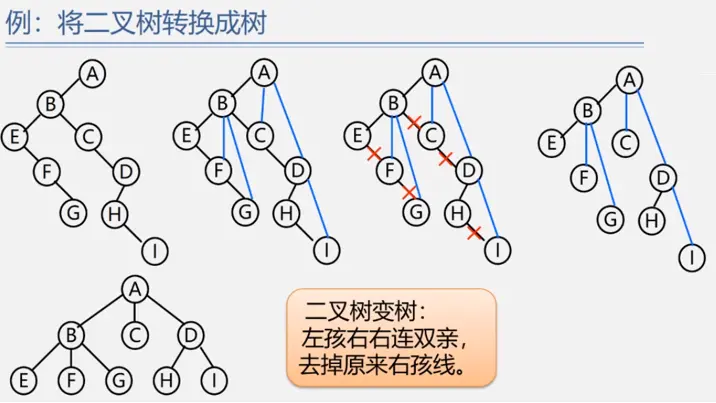
森林与二叉树的相互转换

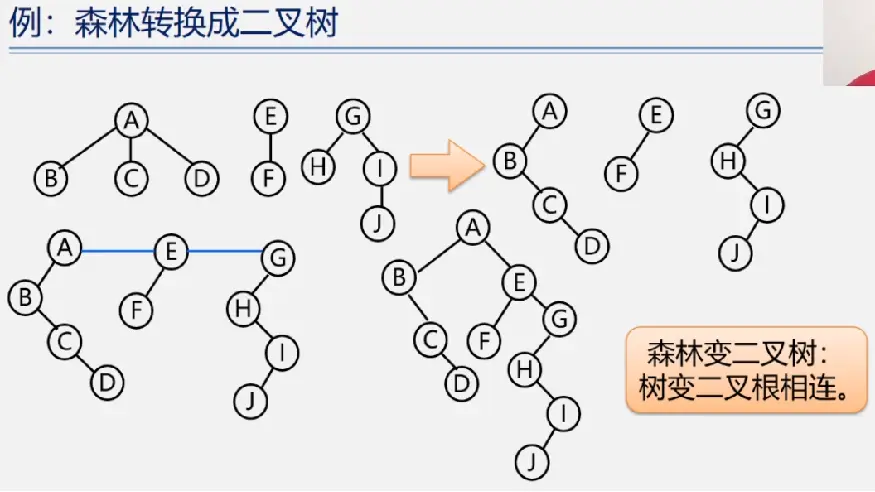
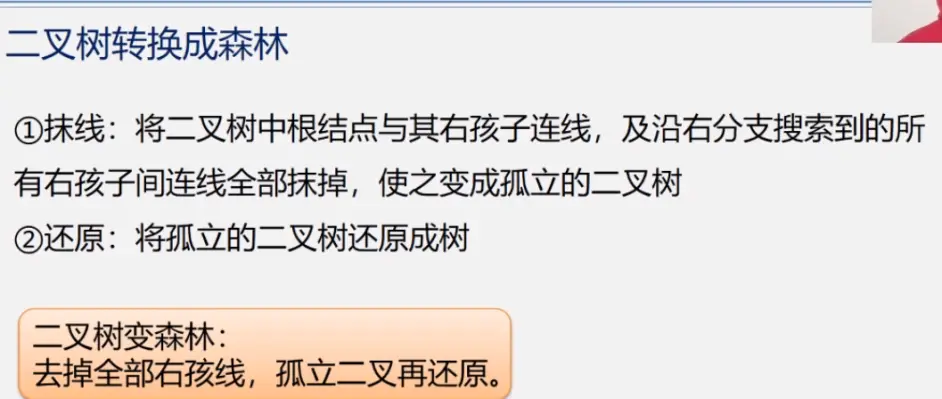
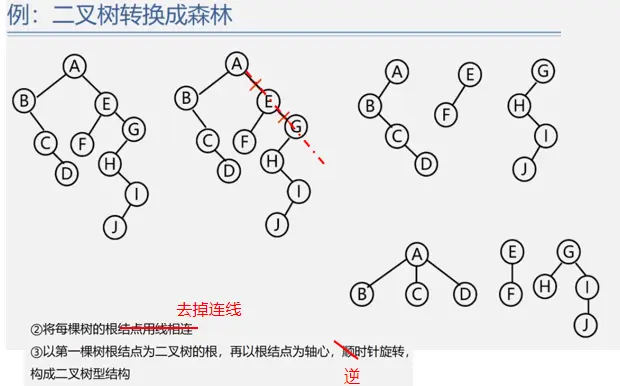
森林的遍历

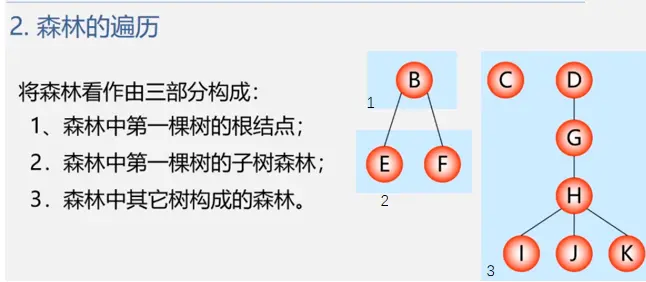

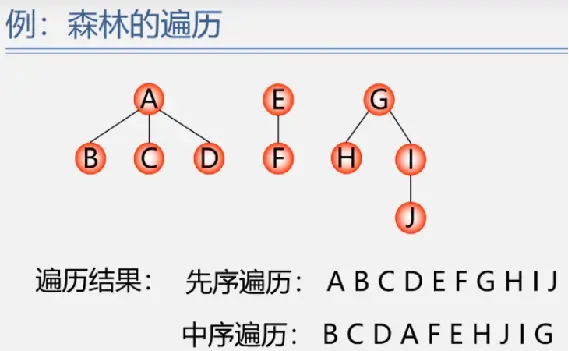
哈夫曼树
引例
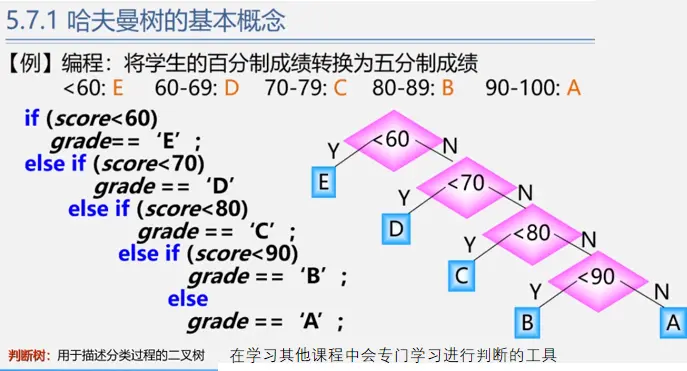
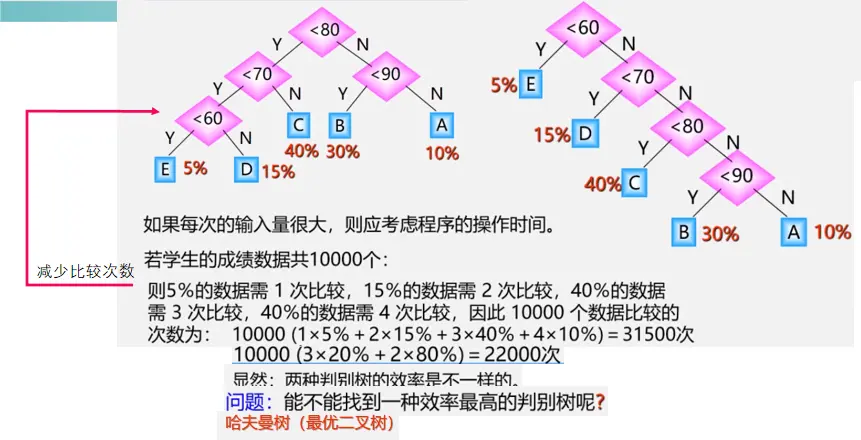
基本概念
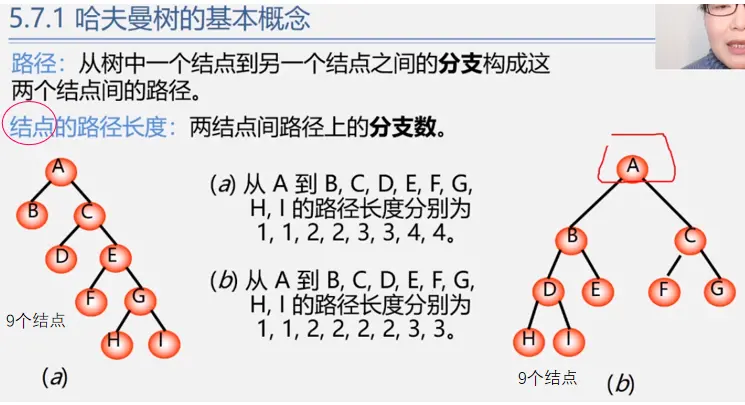
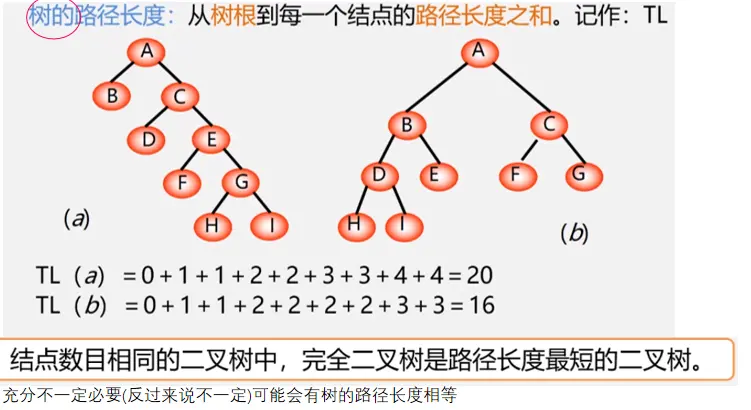
权(weight)又称权重:将树中结点赋给一个有着某种含义的数值,(具体的意义根据树使用的场合确定)则这个数值称为该结点的权。比如之前提到的判断树中5%表示对应分数段人在总人数中的比例
结点的带权路径长度:从根结点到该结点之间的路径长度与结点上权的乘积

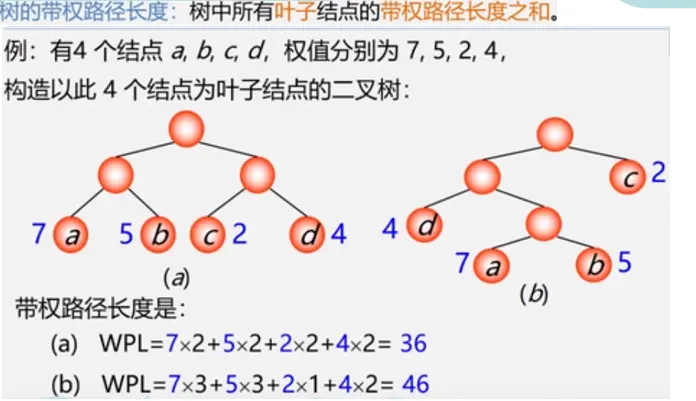
哈夫曼树

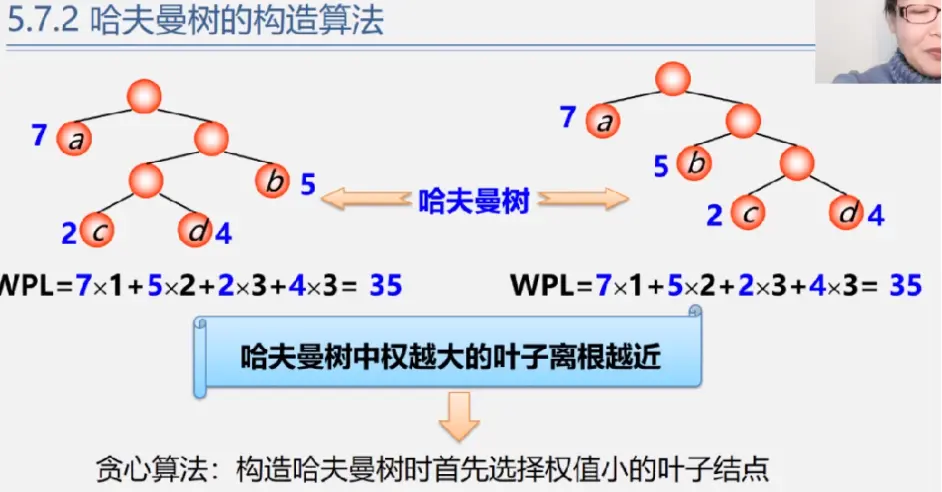
哈夫曼树的构造算法
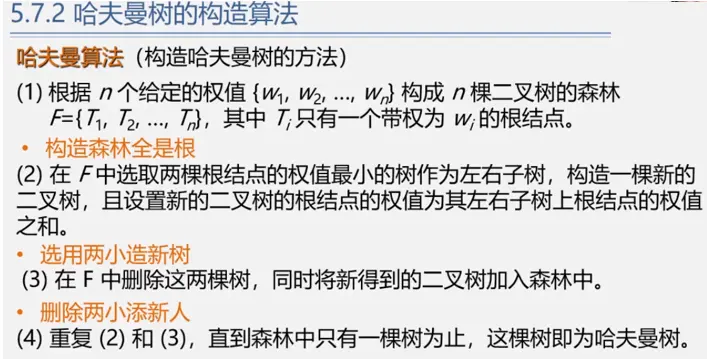
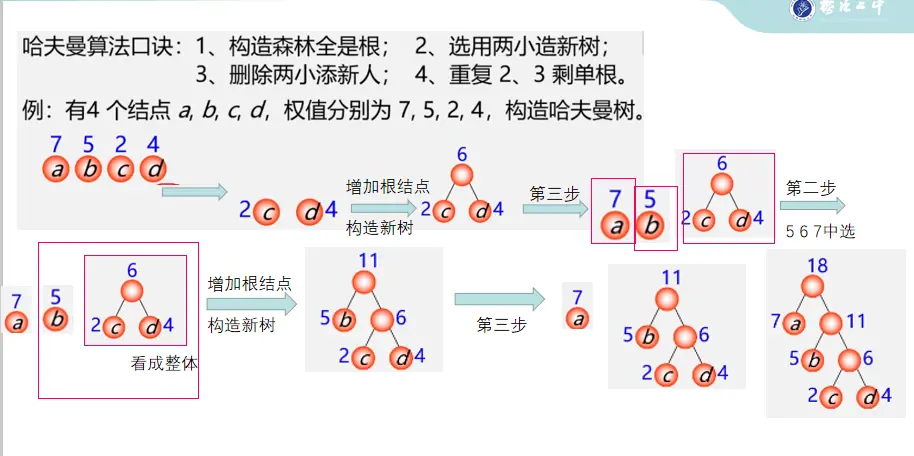
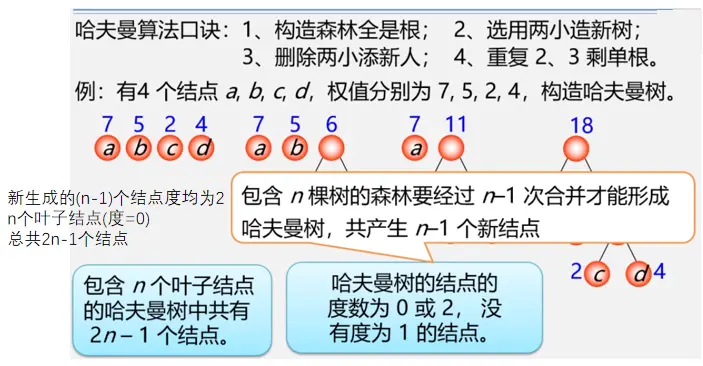
代码实现
顺序二叉树及相关遍历
Java实现
package com.drizzledrop.binaryTree;
public class ArrayBinaryTree {
int []data;
public ArrayBinaryTree(int []data){
this.data = data;
}
public void frontShow(){
frontShow(0);
}
public void midShow(){
midShow(0);
}
public void afterShow(){
afterShow(0);
}
// 前序遍历
public void frontShow(int index){
if(data == null || data.length == 0){
return;
}
// 先遍历当前节点的内容
System.out.print(data[index] + " ");
// 处理左子树
if(2 * index + 1 < data.length){
frontShow(2 * index + 1);
}
// 处理右子树
if(2 * index + 2 < data.length){
frontShow(2 * index + 2);
}
}
// 中序遍历
public void midShow(int index){
if(data == null || data.length == 0){
return;
}
// 左
if(2 * index + 1 < data.length) {
midShow(2 * index + 1);
}
// 根
System.out.print(data[index] + " ");
// 右
if(2 * index + 2< data.length){
midShow(2 * index + 2);
}
}
// 后序遍历
public void afterShow(int index){
if(data == null || data.length == 0){
return;
}
// 左
if(2 * index + 1 < data.length){
afterShow(2 * index + 1);
}
// 右
if(2 * index + 2< data.length){
afterShow(2 * index + 2);
}
// 根
System.out.print(data[index] + " ");
}
}
package com.drizzledrop.binaryTree;
public class TestArrayBinaryTree {
public static void main(String[] args) {
int []data = new int[]{1,2,3,4,5,6,7}; //创建二叉树方便,一般用于满二叉树
ArrayBinaryTree tree = new ArrayBinaryTree(data);
/* 顺序二叉树如下:
* 1
* 2 3
* 4 5 6 7
* */
System.out.print("先序遍历:");
tree.frontShow();// 先序遍历:1 2 4 5 3 6 7
System.out.println();
System.out.print("中序遍历:");
tree.midShow();// 中序遍历:4 2 5 1 6 3 7
System.out.println();
System.out.print("后序遍历:");
tree.afterShow();// 后序遍历:4 5 2 6 7 3 1
}
}
链表二叉树及相关遍历
C++实现
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
class TreeNode {
public:
int value;
TreeNode* leftNode;
TreeNode* rightNode;
public:
TreeNode(int value)
:value(value), leftNode(nullptr), rightNode(nullptr) {}
TreeNode() {}
~TreeNode() {
if (leftNode != nullptr)delete leftNode;
if (rightNode != nullptr)delete rightNode;
}
void setLeftNode(TreeNode* leftNode) {
this->leftNode = leftNode;
}
int getValue() {
return this->value;
}
void setRightNode(TreeNode* rightNode) {
this->rightNode = rightNode;
}
void frontShow() {
printf("%d ", value);
if (leftNode != nullptr) { leftNode->frontShow(); }
if (rightNode != nullptr) { rightNode->frontShow(); }
}
void midShow() {
if (leftNode != nullptr) { leftNode->midShow(); }
printf("%d ", value);
if (rightNode != nullptr) { rightNode->midShow(); }
}
void afterShow() {
if (leftNode != nullptr) { leftNode->afterShow(); }
if (rightNode != nullptr) { rightNode->afterShow(); }
printf("%d ", value);
}
TreeNode* frontSearch(int i) {
TreeNode* target = nullptr;
if (value == i) return this;
else {
if (leftNode != nullptr) target = leftNode->frontSearch(i);
if (target != nullptr) return target;
if (rightNode != nullptr) target = rightNode->frontSearch(i);
}
return target;
}
};
class ListBinaryTree {
private:
TreeNode* root;
public:
ListBinaryTree(TreeNode* root)
:root(root)
{}
ListBinaryTree() {}
void setRoot(TreeNode* root) {
this->root = root;
}
TreeNode* getRoot() {
return root;
}
void frontShow() {
if (root != nullptr) root->frontShow();
cout << endl;
}
void midShow() {
if (root != nullptr) root->midShow();
cout << endl;
}
void afterShow() {
if (root != nullptr) root->afterShow();
cout << endl;
}
TreeNode* frontSearch(int i) {
return root->frontSearch(i);
}
void frontStackShow() {
TreeNode* item = root;
stack<TreeNode*> s;
while (item != nullptr || !s.empty()) {
while (item != nullptr) {
cout << item->value << " ";
s.push(item);
item = item->leftNode;
}
if (!s.empty()) {
item = s.top();
s.pop();
item = item->rightNode;
}
}
cout << endl;
}
void midStackShow() {
TreeNode* item = root;
stack<TreeNode*> s;
while (item != nullptr || !s.empty()) {
while (item != nullptr) {
s.push(item);
item = item->leftNode;
}
if (!s.empty()) {
item = s.top();
cout << item->value << " ";
s.pop();
item = item->rightNode;
}
}
cout << endl;
}
void afterStackShow() {
TreeNode* item = root;
stack<TreeNode*> s;
stack<int> support;
while (item != nullptr || !s.empty()) {
while (item != nullptr) {
support.push(item->value);
s.push(item);
item = item->rightNode;
}
if (!s.empty()) {
item = s.top();
s.pop();
item = item->leftNode;
}
}
while (!support.empty()) {
cout << support.top() << " ";
support.pop();
}
cout << endl;
}
void levelShow() {
queue<TreeNode*> q;
TreeNode* item = root;
if (item == nullptr) return;
q.push(item);
while (!q.empty()) {
item = q.front();
q.pop();
cout << item->value << " ";
if (item->leftNode != nullptr) q.push(item->leftNode);
if (item->rightNode != nullptr) q.push(item->rightNode);
}
}
int getNodeNumb() {
int numb = 0;
TreeNode* item = root;
stack<TreeNode*> s;
while (item != nullptr || !s.empty()) {
while (item != nullptr) {
s.push(item);
item = item->leftNode;
}
if (!s.empty()) {
item = s.top();
numb++;
s.pop();
item = item->rightNode;
}
}
return numb;
}
int getLearNodeNumb() {
int numb = 0;
TreeNode* item = root;
stack<TreeNode*> s;
while (item != NULL || !s.empty()) {
while (item != nullptr) {
s.push(item);
item = item->leftNode;
}
if (!s.empty()) {
item = s.top();
if (item == nullptr) numb++;
s.pop();
item = item->rightNode;
}
}
return numb;
}
int getMaxDepth() {
if (root == nullptr) return 0;
queue<TreeNode*>q;
q.push(root);
int depth = 0;
while (!q.empty()) {
int levelNodeNumb = q.size();
while (levelNodeNumb > 0) {
TreeNode* node = q.front();
q.pop();
if (node->leftNode != nullptr) q.push(node->leftNode);
if (node->rightNode != nullptr) q.push(node->rightNode);
levelNodeNumb--;
}
depth++;
}
return depth;
}
void invertTree() {
TreeNode* goal = root;
stack<TreeNode*>s;
s.push(goal);
while (!s.empty()) {
goal = s.top();
s.pop();
if (goal == nullptr) continue;
if (goal->leftNode == nullptr && goal->rightNode == nullptr) continue;
s.push(goal->leftNode);
s.push(goal->rightNode);
TreeNode* temp = goal->leftNode;
goal->leftNode = goal->rightNode;
goal->rightNode = temp;
}
}
};
int main(void) {
ListBinaryTree* binTree = new ListBinaryTree();
TreeNode* root = new TreeNode(1);
binTree->setRoot(root);
TreeNode* rootL1 = new TreeNode(2);
TreeNode* rootR1 = new TreeNode(3);
root->setLeftNode(rootL1);
root->setRightNode(rootR1);
TreeNode* rootL2 = new TreeNode(4);
TreeNode* rootR2 = new TreeNode(5);
TreeNode* rootL3 = new TreeNode(6);
TreeNode* rootR3 = new TreeNode(7);
rootL1->setLeftNode(rootL2);
rootL1->setRightNode(rootR2);
rootR1->setLeftNode(rootL3);
rootR1->setRightNode(rootR3);
cout << "前序遍历如下:";
binTree->frontStackShow();
binTree->frontShow();
binTree->afterStackShow();
binTree->afterShow();
binTree->invertTree();
binTree->afterStackShow();
return 0;
}
JAVA实现
package com.drizzledrop.binaryTree;
// 树的节点
public class TreeNode {
int value;
TreeNode leftNode;
TreeNode rightNode;
public TreeNode(int value){
this.value = value;
}
// 设置左儿子
public void setLeftNode(TreeNode leftNode){
this.leftNode = leftNode;
}
// 设置右儿子
public void setRightNode(TreeNode rightNode){
this.rightNode = rightNode;
}
// 前序遍历
public void frontShow(){
System.out.print(value + " ");
if(leftNode != null){
leftNode.frontShow();
}
if(rightNode != null){
rightNode.frontShow();
}
}
// 中序遍历
public void midShow(){
if(leftNode != null){
leftNode.midShow();
}
System.out.print(value + " ");
if(rightNode != null){
rightNode.midShow();
}
}
// 后序遍历
public void afterShow(){
if(leftNode != null){
leftNode.afterShow();
}
if(rightNode != null){
rightNode.afterShow();
}
System.out.print(value + " ");
}
// 前序查找
public TreeNode frontSearch(int i){
TreeNode target = null;
if(this.value == i){
return this;
}
else{
if(leftNode != null){
target = leftNode.frontSearch(i);
}
if(target != null){
return target;
}
if(rightNode != null){
target = rightNode.frontSearch(i);
}
}
return target;
}
// 删除一棵子树
public void delete(int i){
TreeNode parent = this;
if(parent.leftNode != null && parent.leftNode.value == i){
parent.leftNode = null;
return;
}
if(parent.rightNode != null && parent.rightNode.value == i){
parent.rightNode = null;
return;
}
parent = leftNode;
if(parent != null){
parent.delete(i);
}
parent = rightNode;
if(parent != null){
parent.delete(i);
}
}
}
package com.drizzledrop.binaryTree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class ListBinaryTree {
TreeNode root;
// 设置根节点
public void setRoot(TreeNode root){
this.root = root;
}
// 返回根节点
public TreeNode getRoot(){
return root;
}
// 前序遍历(递归)
public void frontShow(){
if(root != null){
root.frontShow();
}
}
// 中序遍历
public void midShow(){
if(root != null){
root.midShow();
}
}
// 后序遍历
public void afterShow(){
if(root != null){
root.afterShow();
}
}
// 前序查找
public TreeNode frontSearch(int i){
return root.frontSearch(i);
}
// 前序遍历(非递归,采用栈)
public void frontStackShow(){
TreeNode item = root;
Stack<TreeNode> S = new Stack<>();
while (item != null || !S.isEmpty()) {
while(item != null){
System.out.print(item.value + " ");
S.push(item);
item = item.leftNode;
}
if(!S.isEmpty()){
item = S.pop();
item = item.rightNode;
}
}
}
// 中序遍历(非递归,采用栈)
public void midStackShow(){
TreeNode item = root;
Stack<TreeNode> S = new Stack<>();
while (item != null || !S.isEmpty()) {
while(item != null){
S.push(item);
item = item.leftNode;
}
if(!S.isEmpty()){
item = S.pop();
System.out.print(item.value + " ");
item = item.rightNode;
}
}
}
// 后续遍历(非递归,基于栈,相比于前序和中序的,这里需要以“根 右 左”的方式入栈,即需要一个辅助栈作判断)
public void afterStackShow(){
TreeNode item = root;
Stack<TreeNode> S = new Stack<>();
Stack<Integer> Support = new Stack<>();
while (item != null || !S.isEmpty()) {
while(item != null){
Support.push(item.value);
S.push(item);
item = item.rightNode;
}
if(!S.isEmpty()){
item = S.pop();
item = item.leftNode;
}
}
while(!Support.isEmpty()){
System.out.print(Support.pop() + " ");
}
}
// 层序遍历
public void levelShow(){
Queue<TreeNode> S = new LinkedList<>();
TreeNode item = root;
if(item == null) return;
S.add(root);
while(!S.isEmpty()){
item = S.poll();
System.out.print(item.value + " ");
if(item.leftNode != null){
S.add(item.leftNode);
}
if(item.rightNode != null){
S.add(item.rightNode);
}
}
}
//删除一棵子树
public void delete(int i){
if(root.value == i){
root = null;
}
else{
root.delete(i);
}
}
// 求二叉树结点个数
public int getNodeNumb(){
// 借助中序遍历来求结点个数
int numb = 0;
TreeNode item = root;
Stack<TreeNode> S = new Stack<>();
while (item != null || !S.isEmpty()) {
while(item != null){
S.push(item);
item = item.leftNode;
}
if(!S.isEmpty()){
item = S.pop();
numb++;
item = item.rightNode;
}
}
return numb;
}
// 求叶子结点个数
public int getLearNodeNumb(){
int numb = 0;
// 借由中序遍历来求叶子结点个数
TreeNode item = root;
Stack<TreeNode> S = new Stack<>();
while (item != null || !S.isEmpty()) {
while(item != null){
S.push(item);
item = item.leftNode;
}
if(!S.isEmpty()){
item = S.pop();
item = item.rightNode;
if(item == null) numb++;
}
}
return numb;
}
// 二叉树最大深度
public int getMaxDepth(){
if (root == null) return 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
// 借用层次遍历完成
while (!queue.isEmpty()){
//得到这一层的node个数
int levelNodeSize = queue.size();
//取完这一层,并下一层的node也就全部放进去
while (levelNodeSize > 0){
TreeNode node = queue.poll();
if(node.leftNode != null)
queue.offer(node.leftNode);
if(node.rightNode != null){
queue.offer(node.rightNode);
}
levelNodeSize--;
}
depth++;
}
return depth;
}
// 翻转二叉树
public void invertTree() {
TreeNode goal = root;
Stack<TreeNode> stack = new Stack<>();
stack.push(goal);
while(!stack.isEmpty()){
goal = stack.pop();
if(goal == null) continue;
if(goal.leftNode == null && goal.rightNode == null) continue;
stack.push(goal.rightNode);
stack.push(goal.leftNode);
TreeNode temp = goal.leftNode;
goal.leftNode = goal.rightNode;
goal.rightNode = temp;
}
}
}
package com.drizzledrop.binaryTree;
public class TestListBinaryTree {
public static void main(String[] args) {
ListBinaryTree binTree = new ListBinaryTree();
TreeNode root = new TreeNode(1);
binTree.setRoot(root);
TreeNode rootL1 = new TreeNode(2);
TreeNode rootR1 = new TreeNode(3);
root.setLeftNode(rootL1);
root.setRightNode(rootR1);
TreeNode rootL2 = new TreeNode(4);
TreeNode rootR2 = new TreeNode(5);
TreeNode rootL3 = new TreeNode(6);
TreeNode rootR3 = new TreeNode(7);
rootL1.setLeftNode(rootL2);
rootL1.setRightNode(rootR2);
rootR1.setLeftNode(rootL3);
rootR1.setRightNode(rootR3);
/*
* 1
* 2 3
* 4 5 6 7
*
* */
System.out.print("前序遍历:");
binTree.frontShow();// 前序遍历:1 2 4 5 3 6 7
System.out.println();
System.out.print("前序遍历(非递归,基于栈)");
binTree.frontStackShow();
System.out.println();
System.out.print("中序遍历:");
binTree.midShow();// 中序遍历:4 2 5 1 6 3 7
System.out.println();
System.out.print("中序遍历(非递归,基于栈):");
binTree.midStackShow();
System.out.println();
System.out.print("后序遍历:");
binTree.afterShow();// 后序遍历:4 5 2 6 7 3 1
System.out.println();
System.out.print("后序遍历(非递归,基于栈):");
binTree.afterStackShow();
System.out.println();
System.out.print("层序遍历(基于队列):");
binTree.levelShow();
System.out.println();
// System.out.print("前序查找:");
//// TreeNode result = binTree.frontSearch(6);// 前序查找:com.drizzledrop.binaryTree.TreeNode@1b6d3586
//// System.out.println(result);
//// binTree.delete(3);
//// System.out.print("删除3之后的前序遍历:");
//// binTree.frontShow();// 删除3之后的前序遍历:1 2 4 5
System.out.println(binTree.getNodeNumb()); // 获取结点总数
System.out.println(binTree.getLearNodeNumb()); // 获取叶子结点总数
System.out.println(binTree.getMaxDepth()); // 获取最大深度
binTree.invertTree(); // 翻转二叉树
binTree.frontStackShow(); // 前序遍历
}
}
哈夫曼树Java实现
package com.drizzledrop.HuffmanTree;
//为了让Node对象持续排序Collections集合排序,让Node对象实现Comparable接口
public class Node implements Comparable<Node>{
int value; //节点的权值
Node left; //指向左子节点
Node right; //指向右子节点
public Node() {
}
public Node(int value) {
this.value = value;
}
//写一个前序遍历哈夫曼树的方法
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
@Override
public int compareTo(Node o) {
//从小到大排序
return this.value - o.value;
}
}
package com.drizzledrop.HuffmanTree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
Node root = null;
public HuffmanTree(int[] arr) {
List<Node> nodes = new ArrayList<Node>();
//遍历arr数组,将arr数组中的每个元素构成一个Node对象,然后将Node放入到ArrayList中
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//排序,从小到大
Collections.sort(nodes);
//System.out.println(nodes);
//取出根节点权值最小的两颗二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//从ArrayList中删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
//将parent加入到nodes中
nodes.add(parent);
}
//System.out.println(nodes);
//返回哈夫曼树的根节点
this.root = nodes.get(0);
}
//前序遍历
public void preOrder() {
if (root != null) {
root.preOrder();
} else {
System.out.println("空树,无法遍历");
}
}
/**
* 创建一个HuffmanTree的方法
*
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好后哈夫曼树的根节点
*/
public Node huffmanTree(int[] arr) {
List<Node> nodes = new ArrayList<Node>();
//遍历arr数组,将arr数组中的每个元素构成一个Node对象,然后将Node放入到ArrayList中
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//排序,从小到大
Collections.sort(nodes);
//System.out.println(nodes);
//取出根节点权值最小的两颗二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//从ArrayList中删除处理过的二叉树
nodes.remove(leftNode);
//将parent加入到nodes中
nodes.remove(rightNode);
nodes.add(parent);
}
//System.out.println(nodes);
//返回哈夫曼树的根节点
return nodes.get(0);
}
}
package com.drizzledrop.HuffmanTree;
public class TestHuffmanTree {
public static void main(String[] args) {
int[] arr = {3,8,7,2,5};
HuffmanTree root = new HuffmanTree(arr);
root.preOrder();
}
}
哈夫曼编码实现
package com.drizzledrop.HuffmanTreeCode;
public class Node {
public String code = ""; // 节点的哈夫曼编码
public String data = ""; // 节点的数据
public int count; //节点的权值
public Node lChild;
public Node rChild;
public Node(){}
public Node(String data, int count){
this.data = data;
this.count = count;
}
public Node(int count, Node lChild, Node rChild){
this.count = count;
this.lChild = lChild;
this.rChild = rChild;
}
public Node(String data, int count, Node lChild, Node rChild){
this.data = data;
this.count = count;
this.lChild = lChild;
this.rChild = rChild;
}
}
package com.drizzledrop.HuffmanTreeCode;
import java.util.LinkedList;
public class HuffmanCode {
private String str; // 最初用于压缩的字符串
private Node root; // 哈夫曼二叉树的根节点
private boolean flag; // 最新的字符是否存在的标签
private LinkedList<CharData> charList; // 存储不同字符的队列 相同字符存在同一位
private LinkedList<Node> NodeList; // 储存节点的队列
private class CharData {
int num = 1; // 字符个数
char c; // 字符
public CharData(char ch) {
c = ch;
}
}
/**
* 统计出现的字符及其频率
*
* @param str
*/
private void getCharNum(String str) {
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i); // 从给定的字符串中取出字符
flag = true;
for (int j = 0; j < charList.size(); j++) {
CharData data = charList.get(j);
if (ch == data.c) {
// 字符对象链表中有相同字符则将个数加1
data.num++;
flag = false;
break;
}
}
if (flag) {
// 字符对象链表中没有相同字符则创建新对象加如链表
charList.add(new CharData(ch));
}
}
}
/**
* 将出现的字符创建成单个的结点对象
*/
private void creatNodes() {
for (int i = 0; i < charList.size(); i++) {
String data = charList.get(i).c + "";
int count = charList.get(i).num;
Node node = new Node(data, count); // 创建节点对象
NodeList.add(node); // 加入到节点链表
}
}
/**
* 升序排序
*
* @param nodelist
*/
private void Sort(LinkedList<Node> nodelist) {
for (int i = 0; i < nodelist.size() - 1; i++) {
for (int j = i + 1; j < nodelist.size(); j++) {
Node temp;
if (nodelist.get(i).count > nodelist.get(j).count) {
temp = nodelist.get(i);
nodelist.set(i, nodelist.get(j));
nodelist.set(j, temp);
}
}
}
}
/**
* 设置结点的哈夫曼编码
*
* @param root
*/
private void setCode(Node root) {
if (root.lChild != null) {
root.lChild.code = root.code + "0";
setCode(root.lChild);
}
if (root.rChild != null) {
root.rChild.code = root.code + "1";
setCode(root.rChild);
}
}
/**
* 遍历
*
* @param node 节点
*/
private void output(Node node) {
if (node.lChild == null && node.rChild == null) {
System.out.println(node.data + ": " + node.code);
}
if (node.lChild != null) {
output(node.lChild);
}
if (node.rChild != null) {
output(node.rChild);
}
}
/**
* 输出结果字符的哈夫曼编码
*/
public void output() {
output(root);
}
/**
* 构建哈夫曼树
*/
private void creatTree() {
while (NodeList.size() > 1) {// 当节点数目大于一时
// 4.取出权值最小的两个节点,生成一个新的父节点
// 5.删除权值最小的两个节点,将父节点存放到列表中
Node left = NodeList.poll();
Node right = NodeList.poll();
// 在构建哈夫曼树时设置各个结点的哈夫曼编码
left.code = "0";
right.code = "1";
setCode(left);
setCode(right);
int parentWeight = left.count + right.count;// 父节点权值等于子节点权值之和
Node parent = new Node(parentWeight, left, right);
NodeList.addFirst(parent); // 将父节点置于首位
Sort(NodeList); // 重新排序,避免新节点权值大于链表首个结点的权值
}
}
/*
* 构建哈夫曼编码树
* */
public void creatHuffmanTree(String str) {
this.str = str;
NodeList = new LinkedList<Node>();
charList = new LinkedList<CharData>();
// 1.统计字符串中字符以及字符的出现次数
// 以CharData类来统计出现的字符和个数
getCharNum(str);
// 2.根据第一步的结构,创建节点
creatNodes();
// 3.对节点权值升序排序
Sort(NodeList);
// 4.取出权值最小的两个节点,生成一个新的父节点
// 5.删除权值最小的两个节点,将父节点存放到列表中
creatTree();
// 6.重复第四五步,就是那个while循环
// 7.将最后的一个节点赋给根节点
root = NodeList.get(0);
}
/***********************以下是编解码的实现*************************/
private String hfmCodeStr = "";// 哈夫曼编码连接成的字符串
/**
* 编码
*
* @param str
* @return
*/
public String toHufmCode(String str) {
for (int i = 0; i < str.length(); i++) {
String c = str.charAt(i) + "";
search(root, c);
}
return hfmCodeStr;
}
/**
* @param root 哈夫曼树根节点
* @param c 需要生成编码的字符
*/
private void search(Node root, String c) {
if (root.lChild == null && root.rChild == null) {
if (c.equals(root.data)) {
hfmCodeStr += root.code; // 找到字符,将其哈夫曼编码拼接到最终返回二进制字符串的后面
}
}
if (root.lChild != null) {
search(root.lChild, c);
}
if (root.rChild != null) {
search(root.rChild, c);
}
}
// 保存解码的字符串
String result = "";
boolean target = false; // 解码标记
/**
* 解码
*
* @param codeStr
* @return
*/
public String CodeToString(String codeStr) {
int start = 0;
int end = 1;
while (end <= codeStr.length()) {
target = false;
String s = codeStr.substring(start, end);
matchCode(root, s); // 解码
// 每解码一个字符,start向后移
if (target) {
start = end;
}
end++;
}
return result;
}
/**
* 匹配字符哈夫曼编码,找到对应的字符
*
* @param root 哈夫曼树根节点
* @param code 需要解码的二进制字符串
*/
private void matchCode(Node root, String code) {
if (root.lChild == null && root.rChild == null) {
if (code.equals(root.code)) {
result += root.data; // 找到对应的字符,拼接到解码字符穿后
target = true; // 标志置为true
}
}
if (root.lChild != null) {
matchCode(root.lChild, code);
}
if (root.rChild != null) {
matchCode(root.rChild, code);
}
}
}
package com.drizzledrop.HuffmanTreeCode;
public class TestHuffmanCode {
public static void main(String[] args) {
HuffmanCode huff = new HuffmanCode();// 创建哈弗曼对象
String data ="将一个字符串中出现的字符生成其对应的哈夫曼编码,分为以下几步:\n" +
"1. 统计出现的字符及频率\n" +
"2. 将各个字符创建为叶子结点,频率为结点的权值,用链表保存这些叶子结点\n" +
"3. 将结点队列中的结点按权值升序排列\n" +
"4. 取出权值最小的两个结点构建父节点(要从链表中删除取出的结点),将新生成的父节点添加到结点链表,并从新排序\n" +
"5. 重复4步骤,直到只剩下一个结点\n" +
"6. 返回最后的结点,即为哈夫曼树的根节点。";
huff.creatHuffmanTree(data);// 构造树
huff.output(); // 显示字符的哈夫曼编码
// 将目标字符串利用生成好的哈夫曼编码生成对应的二进制编码
String hufmCode = huff.toHufmCode(data);
System.out.println("编码:" + hufmCode);
// 将上述二进制编码再翻译成字符串
System.out.println("解码:" + huff.CodeToString(hufmCode));
}
}
哈夫曼树C++实现
虽然思想一样,但c++的实现没那么复杂,参考了up主臣-信宏
// 哈夫曼编码
#include <iostream>
using namespace std;
// define node of huffman tree
struct HTNode {
int mParent{};
int mRChild{};
int mLChild{};
string data;
string code;
int mWeight{};
};
// define huffman tree
struct HTree {
HTNode *mHTree;
int mLength;
};
// init huffmanTree
void initHTree(HTree &HT, int num) {
int total = num * 2 - 1;
HT.mHTree = new HTNode[total];
if (!HT.mHTree) cout << "init fail" << endl;
HT.mLength = 0;
int i;
for (i = 0; i < num; i++) {
HT.mHTree[i].mLChild = -1;
HT.mHTree[i].mRChild = -1;
HT.mHTree[i].mParent = -1;
cout << "pls input the data and weight of " << i + 1 << endl;
int weight;
string data;
cin >> data >> weight;
HT.mHTree[i].mWeight = weight;
HT.mHTree[i].data = data;
HT.mLength++;
}
for (; i < total; i++) {
HT.mHTree[i].mLChild = -1;
HT.mHTree[i].mRChild = -1;
HT.mHTree[i].mParent = -1;
HT.mHTree[i].mWeight = 65535;
HT.mLength++;
}
cout << "init success" << endl;
}
// find two min node
void findTwoMinNode(HTree &HT, int pos, int &min1, int &min2) {
int i = 0;
int m1, m2;
int minWeight;
// find min1
while (HT.mHTree[i].mParent != -1) i++;
minWeight = HT.mHTree[i].mWeight;
m1 = i;
for (; i < pos; i++) {
if (HT.mHTree[i].mWeight < minWeight && HT.mHTree[i].mParent == -1) {
minWeight = HT.mHTree[i].mWeight;
m1 = i;
}
}
HT.mHTree[m1].mParent = 1;
min1 = m1;
// find min2
i = 0;
while (HT.mHTree[i].mParent != -1) i++;
minWeight = HT.mHTree[i].mWeight;
m2 = i;
for (; i < pos; i++) {
if (HT.mHTree[i].mWeight < minWeight && HT.mHTree[i].mParent == -1) {
minWeight = HT.mHTree[i].mWeight;
m2 = i;
}
}
HT.mHTree[m2].mParent = 1;
min2 = m2;
}
// create huffmanTree
void createHuffmanTree(HTree &HT, int num) {
if (!HT.mHTree) cout << "the tree is not exist" << endl;
int i, min1, min2;
for (i = num; i < HT.mLength; i++) {
findTwoMinNode(HT, i, min1, min2);
HT.mHTree[min1].mParent = i;
HT.mHTree[min2].mParent = i;
HT.mHTree[i].mLChild = min1;
HT.mHTree[i].mRChild = min2;
HT.mHTree[i].mWeight = HT.mHTree[min1].mWeight + HT.mHTree[min2].mWeight;
}
}
//function of huffmanCode
void huffmanCoding(HTree &HT) {
int numOfCode = (HT.mLength + 1) / 2;
char *code = new char[numOfCode];
int cur = HT.mLength - 1;
int codeLen = 0;
//visit state 0:not visited 1:1child visited 2:all visited
int i;
for (i = 0; i < HT.mLength; i++) {
HT.mHTree[i].mWeight = 0;
}
while (cur != -1) {
if (HT.mHTree[cur].mWeight == 0) {
HT.mHTree[cur].mWeight = 1;
if (HT.mHTree[cur].mLChild != -1) {
code[codeLen++] = '0';
cur = HT.mHTree[cur].mLChild;
} else {
code[codeLen] = '\0';
HT.mHTree[cur].code = code;
}
} else {
if (HT.mHTree[cur].mWeight == 1) {
HT.mHTree[cur].mWeight = 2;
if (HT.mHTree[cur].mRChild != -1) {
code[codeLen++] = '1';
cur = HT.mHTree[cur].mRChild;
}
}
else {
HT.mHTree[cur].mWeight = 0;
cur = HT.mHTree[cur].mParent;
--codeLen;
}
}
}
delete[]code;
}
// search data of code
int searchDataOfCode(HTree &HT, string code){
int length = (HT.mLength + 1) / 2;
for(int i = 0; i < length; i++){
if(code == HT.mHTree[i].code) return i;
}
return -1;
}
// decoding code to information
void huffmanDecoding(HTree &HT, string data){
int begin = 0, size, length = data.length();
if(data.length() != 0) size = 1;
while(begin < data.length()){
int goal = searchDataOfCode(HT, data.substr(begin, size));
if(goal != -1) {
cout <<HT.mHTree[goal].data;
begin += size;
size = 1;
}
else size++;
}
}
// show code
void showHuffmanCode(HTree &HT,int numOfCode) {
for (int j = 0; j < numOfCode; j++) {
cout << "the code of " << HT.mHTree[j].data << " is " << HT.mHTree[j].code << endl;
}
}
// list huffmanTree
void showTree(HTree &HT) {
if (HT.mLength != NULL) {
cout << "show the node of huffmanTree " << endl;
for (int i = 0; i < HT.mLength; i++) {
cout << " " << HT.mHTree[i].mParent;
cout << " " << HT.mHTree[i].mLChild;
cout << " " << HT.mHTree[i].mRChild;
cout << " " << HT.mHTree[i].data;
cout << " " << HT.mHTree[i].mWeight << endl;
}
}
}
int main() {
cout << "pls input the num of leaf node\n";
int num;
cin >> num;
HTree myTree{};
initHTree(myTree, num);
createHuffmanTree(myTree, num);
showTree(myTree);
cout << "**************************************************\n";
huffmanCoding(myTree);
showHuffmanCode(myTree, num);
cout << "pls input your code:";
string data;
cin >> data;
huffmanDecoding(myTree, data);
return 0;
}
图
定义
前置知识
整体框架

具体定义
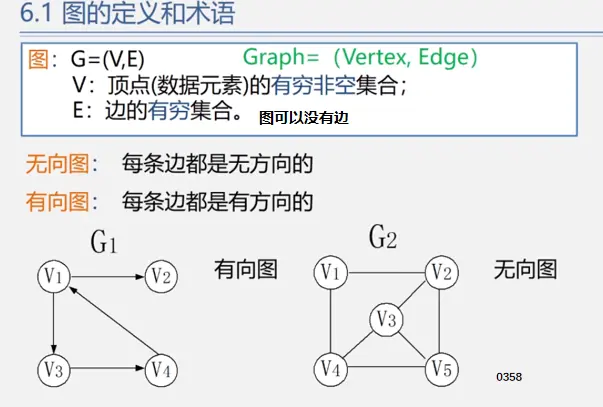
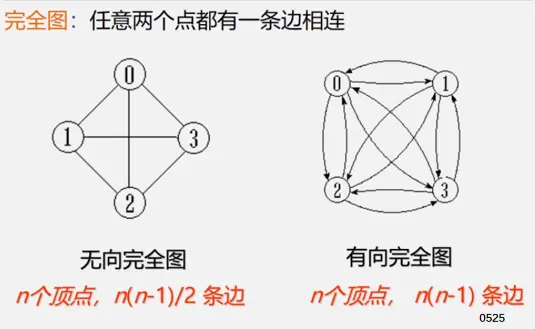

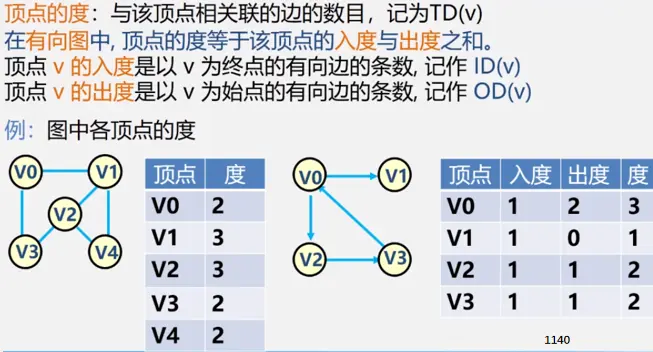
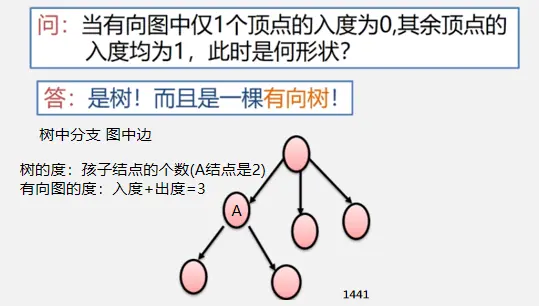
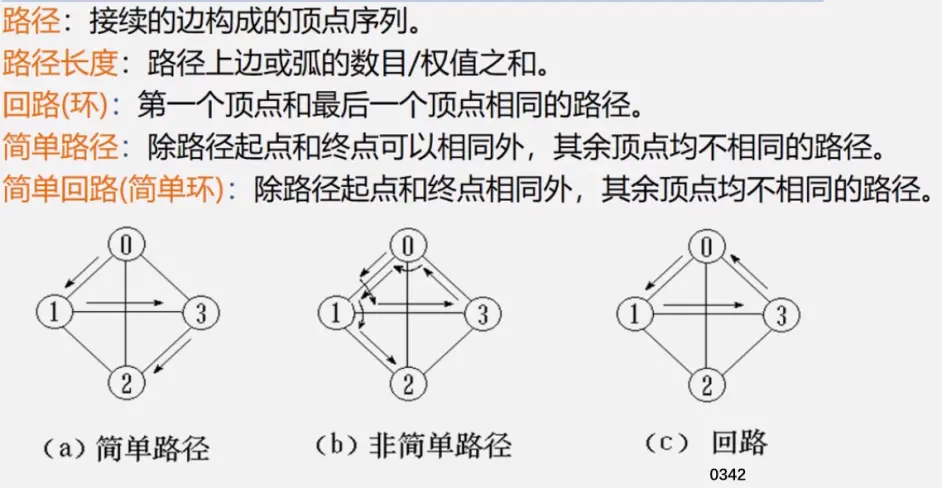
简单路径:好马不吃回头草
简单回路:南辕北辙
连通图指图,强连通图指网

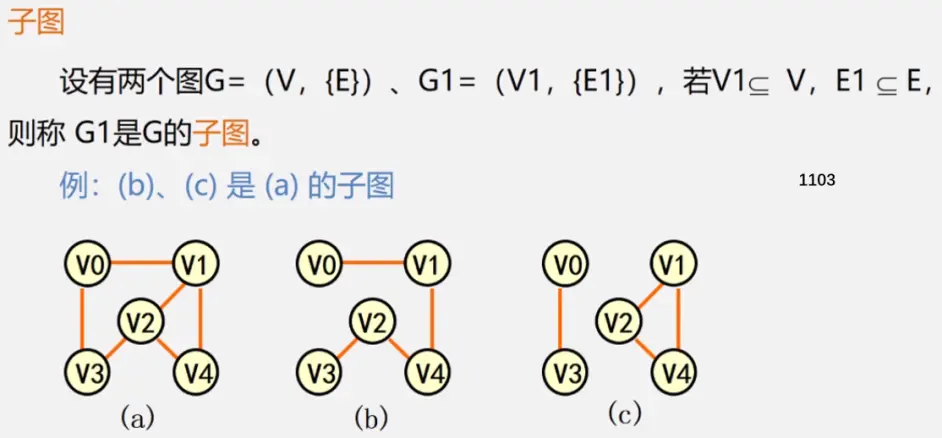
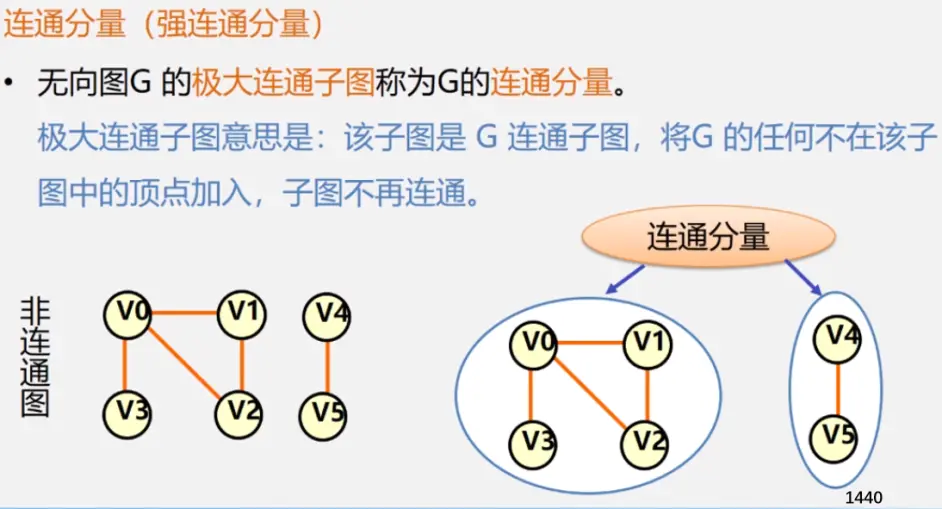
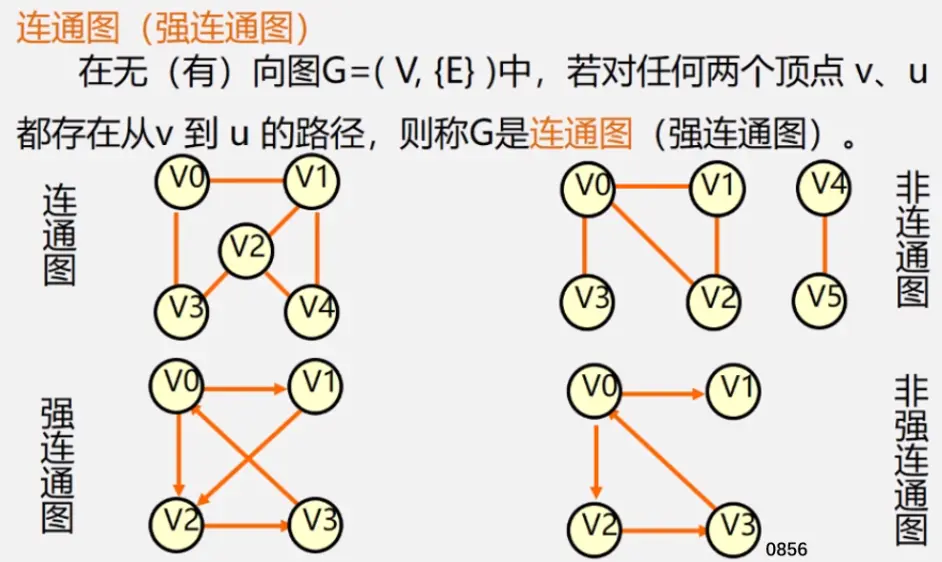
注:极大连通子图要注意是顶点数达到最大,再加一个顶点就不再连通了
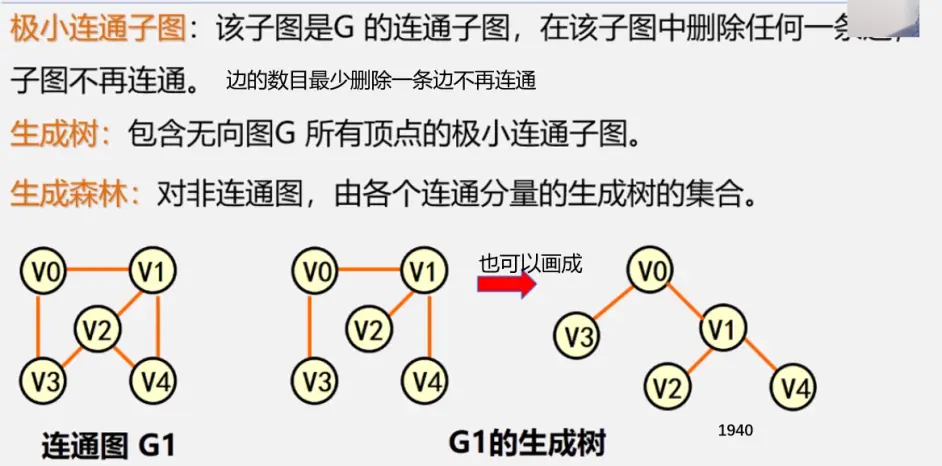
生成树:即该无向图保持连通的边最少的状态
给以上内容的补充:数据结构:图(Graph)【详解】
引例


储存结构
领接矩阵
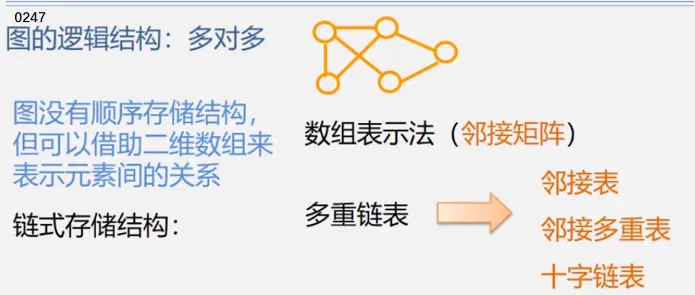
链式:图有多个前驱和多个后继需要多个指针域但图不像线性表一个前驱一个后继用pre和next两个域(双向链表)二叉树一个前驱两个后继用lch和rch(二叉链表)有必要时候可以增加parent(三叉链表)图前驱和后继数量不确定(重点介绍邻接矩阵和邻接表)
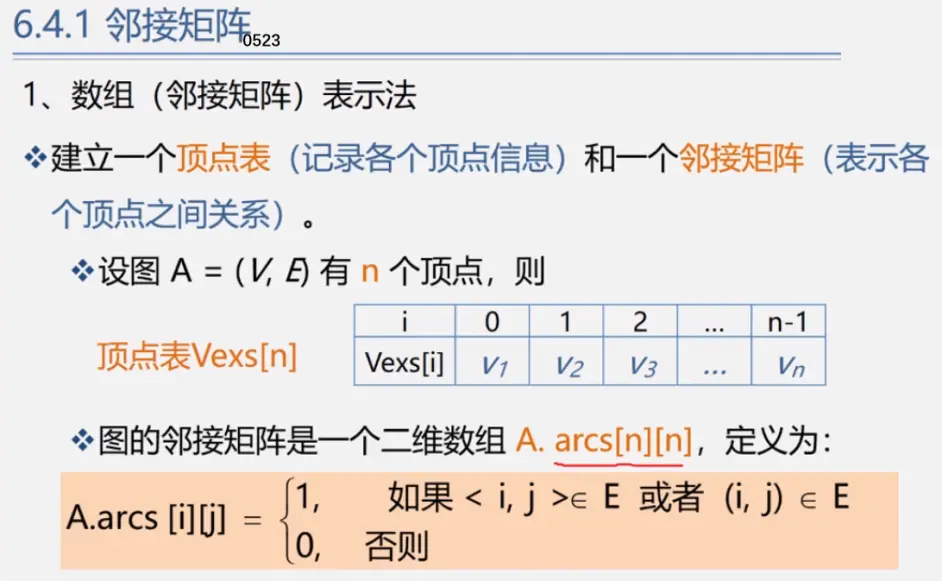
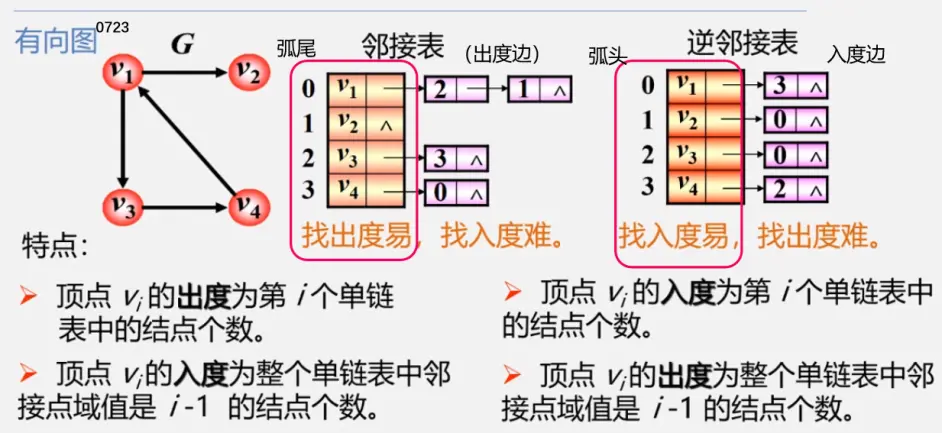
注:()无方向不区分起始端点和终止端点<>有向i(弧尾)-->j(弧头)i出发指向j
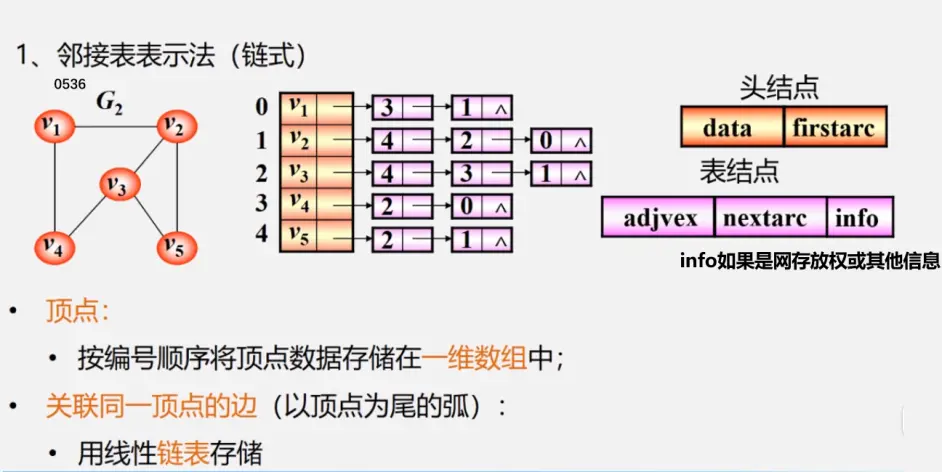
邻接表示两个顶点之间的关系:(有边/弧相连的两个顶点之间的关系)

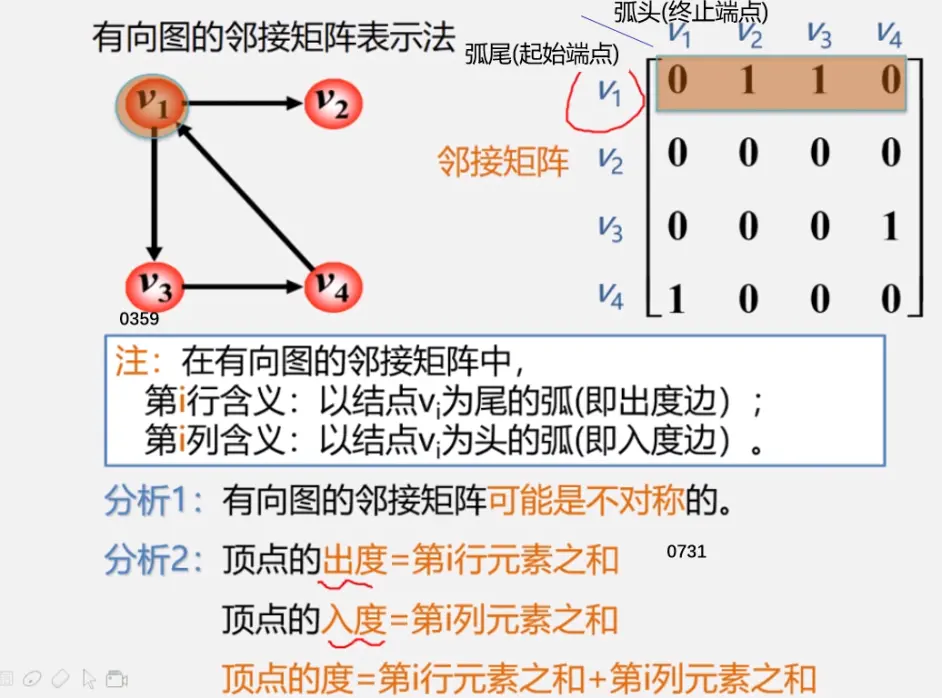
注:行为出度
列为出度
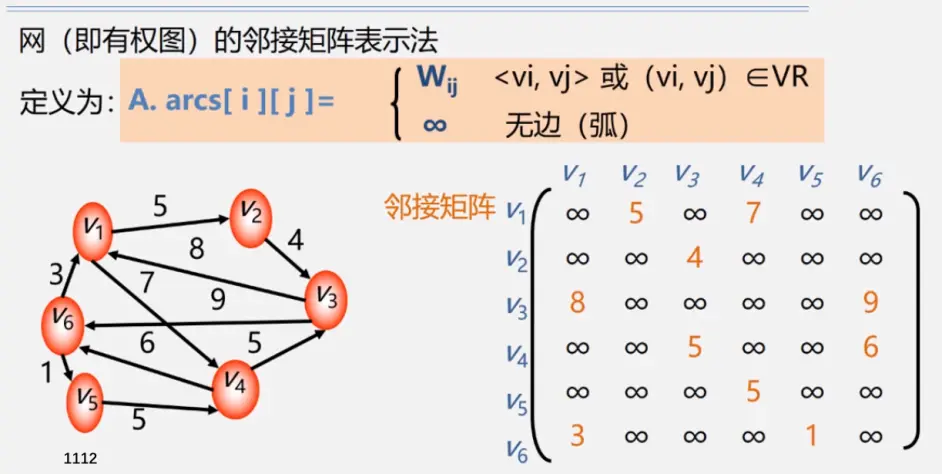


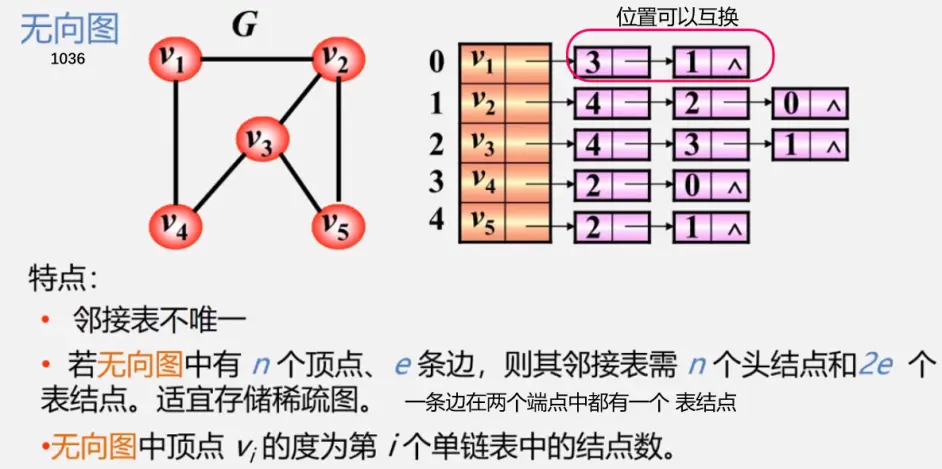
邻接表
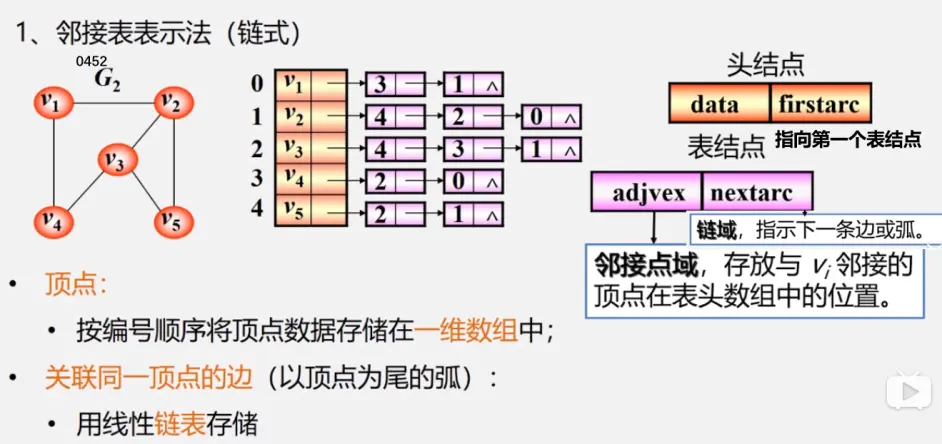
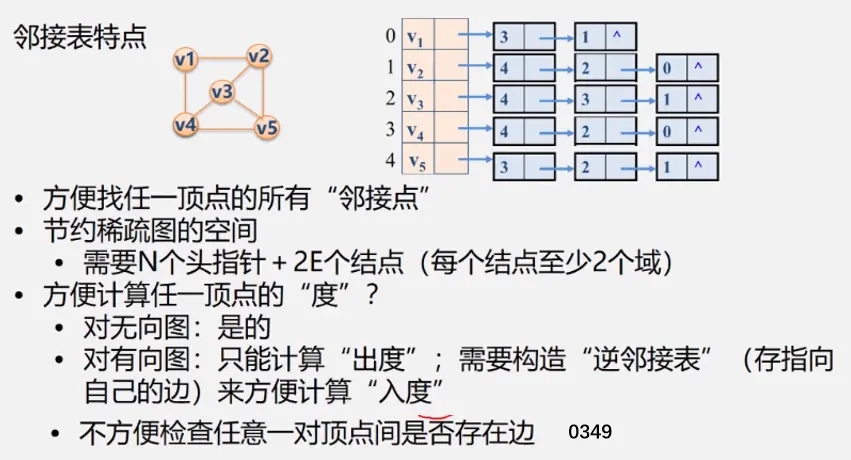
两者关系
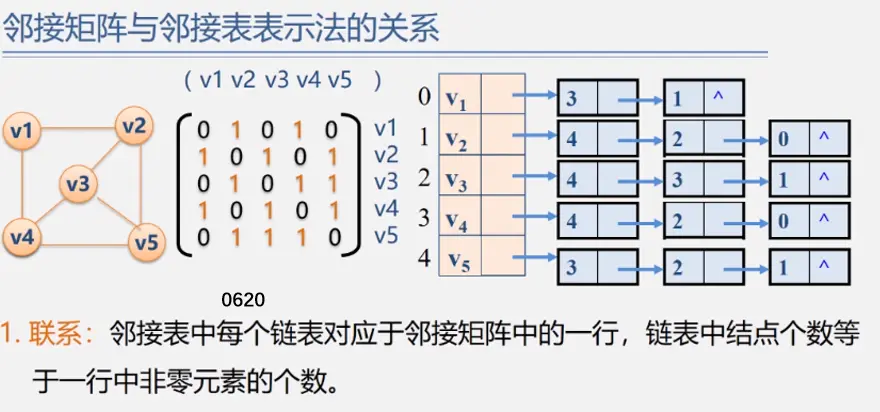

十字链表
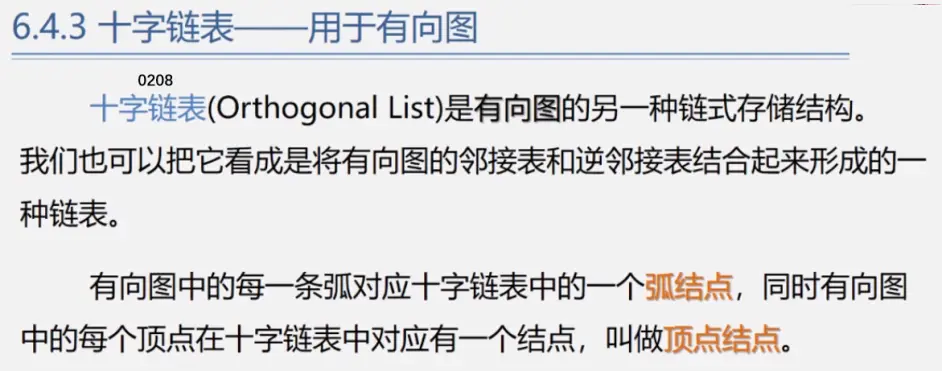
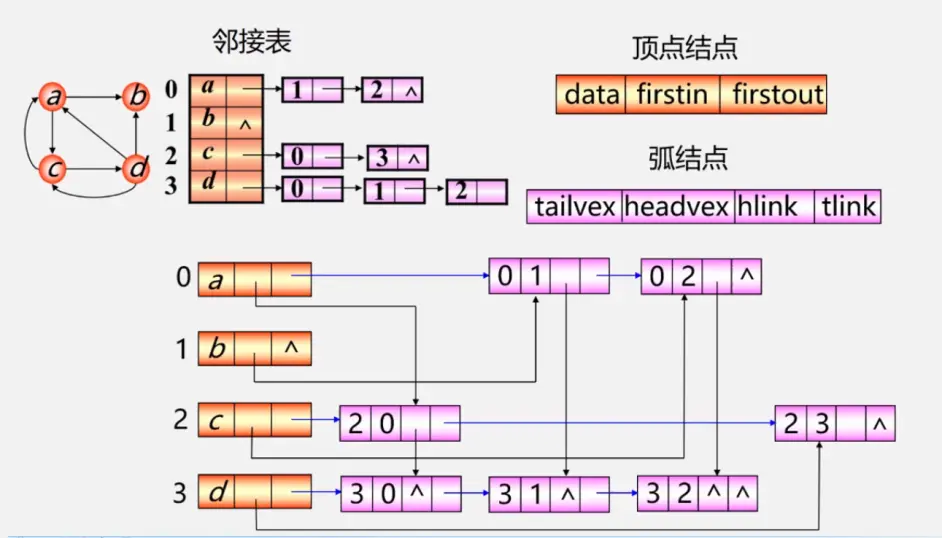
tailvex:弧尾的位置
headvex:弧头的位置
hlink:弧头相同的下一条弧
tlink:弧尾相同的下一条弧
弧节点这些都是啥意思呢?
四个域,第一个弧尾位置,即存放指向来的弧的尾位置
第二个弧头位置类似,即存放指向来的弧的头位置
第三个弧头相同下一条弧,就是指向头相同的下一个弧节点第四个弧尾相同下一条弧,就是指向头相同的下一个弧节点
一定要区分清楚顶点节点和弧节点、搞明白顶点节点和弧节点的每个域都在干啥,画图理解挺好,这里也有一个up主的画图思路 数据结构|十字链表|简单粗暴零失误画出十字链表
邻接多重表
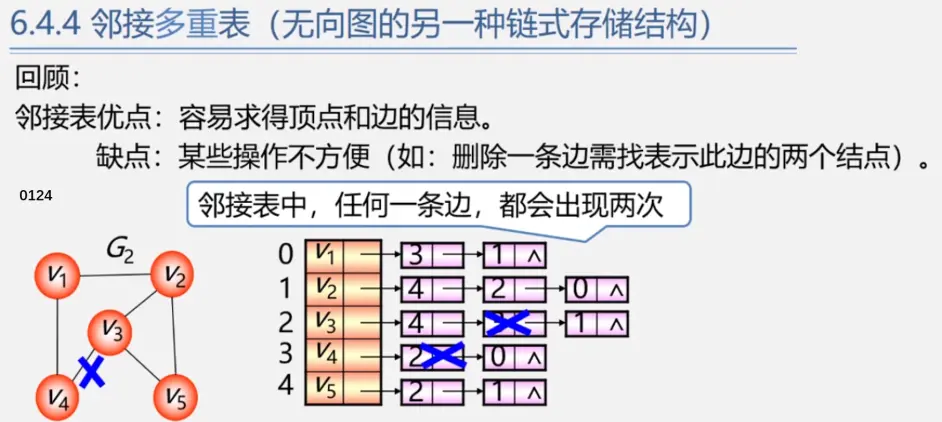
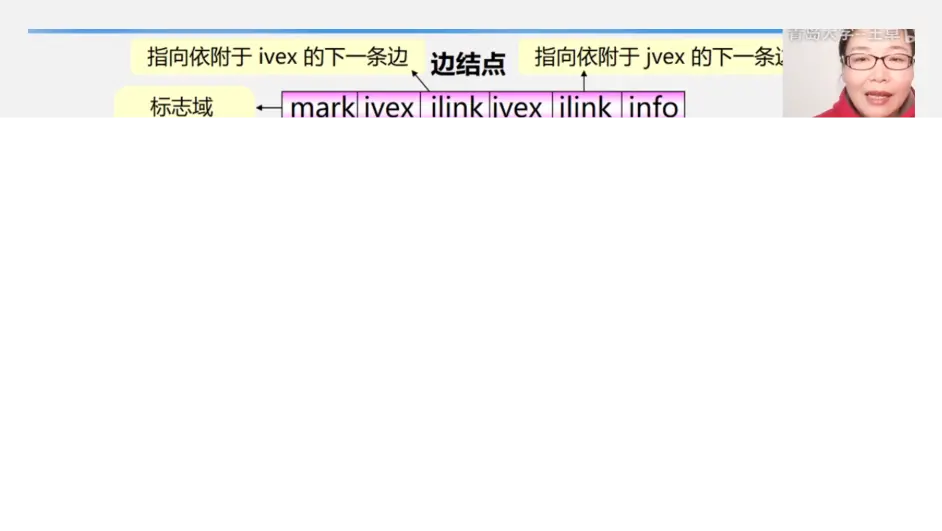
同样是弄清楚顶点节点和边节点各个域在干啥
参考 数据结构---邻接多重表 的画法
遍历
前置知识
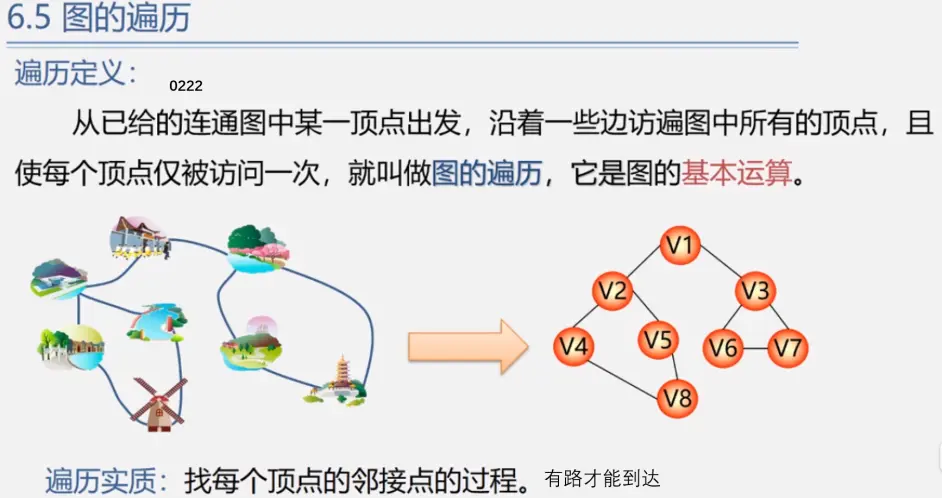

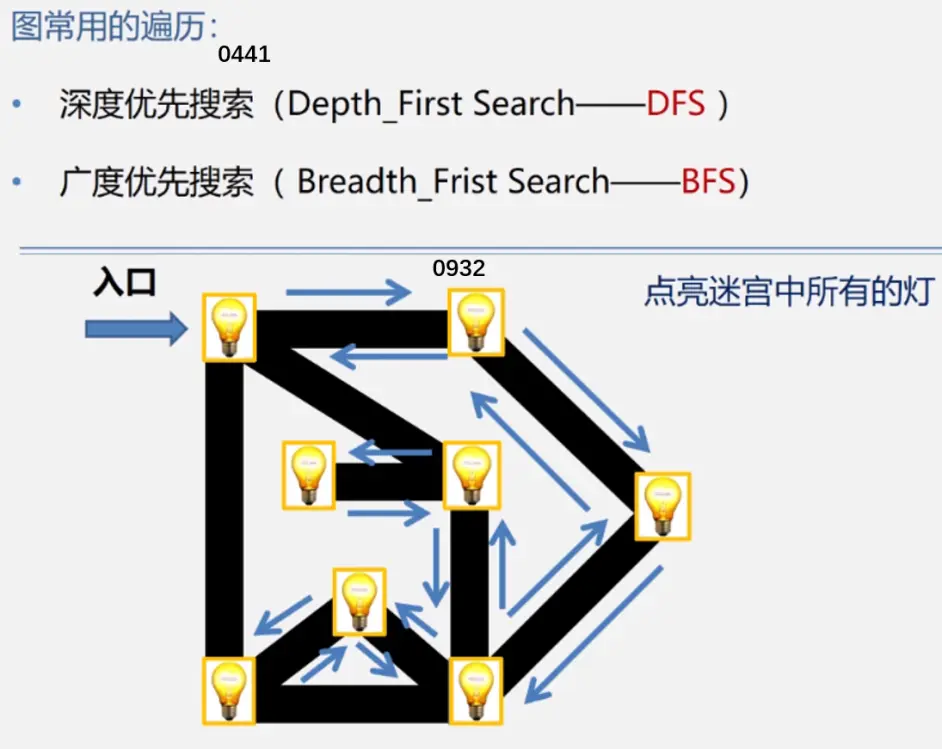
深度优先遍历(DFS)


- 深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点, 可以这样理解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
- 这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。
- 深度优先搜索是一个递归的过程
遍历步骤
- 访问初始结点v,并标记结点v为已访问。
- 查找结点v的第一个邻接结点w。
- 若w存在,则继续执行4,如果w不存在,则回到第1步,将从v的下一个结点继续。
- 若w未被访问,对w进行深度优先遍历递归(即把w当做另一个v,然后进行步骤123)。
- 查找结点v的w邻接结点的下一个邻接结点,转到步骤3。
即:一条路走到黑
广度优先遍历(BFS)
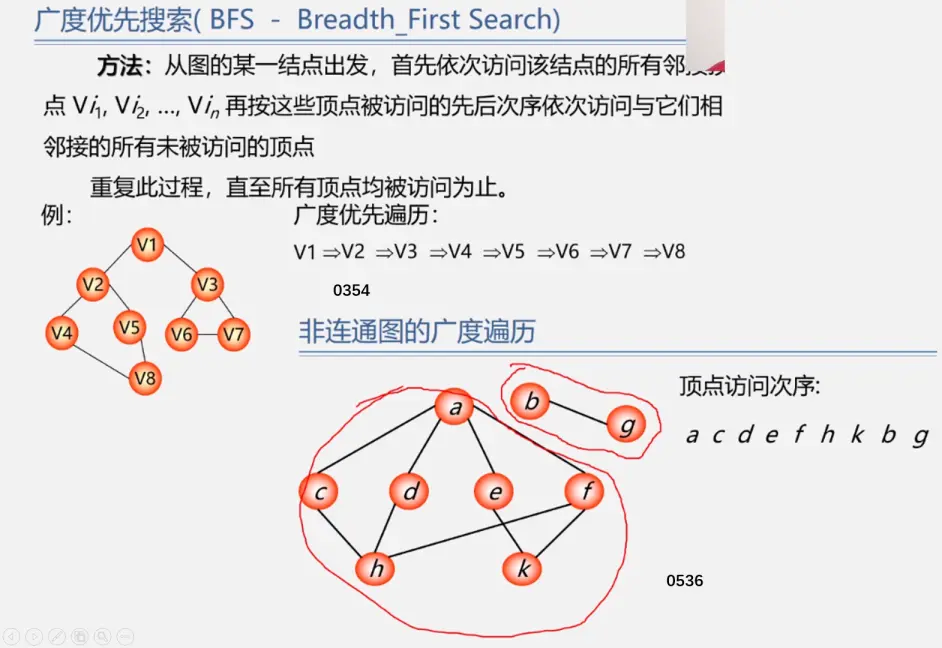
类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点(类似于树的层次遍历?)
遍历步骤
访问初始结点v并标记结点v为已访问。
结点v入队列
当队列非空时,继续执行,否则算法结束。
出队列,取得队头结点u。
查找结点u的第一个邻接结点w。
若结点u的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
6.1 若结点w尚未被访问,则访问结点w并标记为已访问。
6.2 结点w入队列
6.3 查找结点u的继w邻接结点后的下一个邻接结点w,转到步骤6。
即:条条大路找牛马
最小生成树
定义
生成树:即该无向图保持连通的边最少的状态
一个图中可能存在多条相连的边,我们一定可以从一个图中挑出一些边生成一棵树。这仅仅是生成一棵树,还未满足最小,当图中每条边都存在权重时,这时候我们从图中生成一棵树(n - 1 条边)时,生成这棵树的总代价就是每条边的权重相加之和。
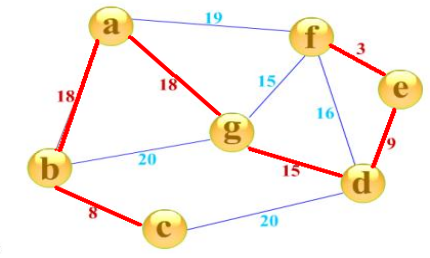
一个有N个点的图,边一定是大于等于N-1条的。图的最小生成树,就是在这些边中选择N-1条出来,连接所有的N个点。这N-1条边的边权之和是所有方案中最小的。
生活应用
- 以有线电视电缆的架设为例,若只能沿著街道布线,则以街道为边,而路口为顶点,其中必然有一最小生成树能使布线成本最低。
最小生成树的两种算法
prim算法
思路:prim算法的核心信仰是:从已知扩散寻找最小。它的实现方式和Dijkstra算法相似但稍微有所区别,Dijkstra是求单源最短路径,而每计算一个点需要对这个点重新更新距离,而prim不用更新距离。直接找已知点的邻边最小加入即可!prim和kruskal算法都是从边入手处理。
除了Kruskal算法以外,普里姆算法(Prim算法)也是常用的最小生成树算法。虽然在效率上差不多。但是贪心的方式和Kruskal完全不同。
算法具体步骤为:
- 寻找图中任意点,以它为起点,它的所有边V加入集合(优先队列)q1,设置一个boolean数组bool[]标记该位置(边有两个点,每次加入没有被标记那个点的所有边)。
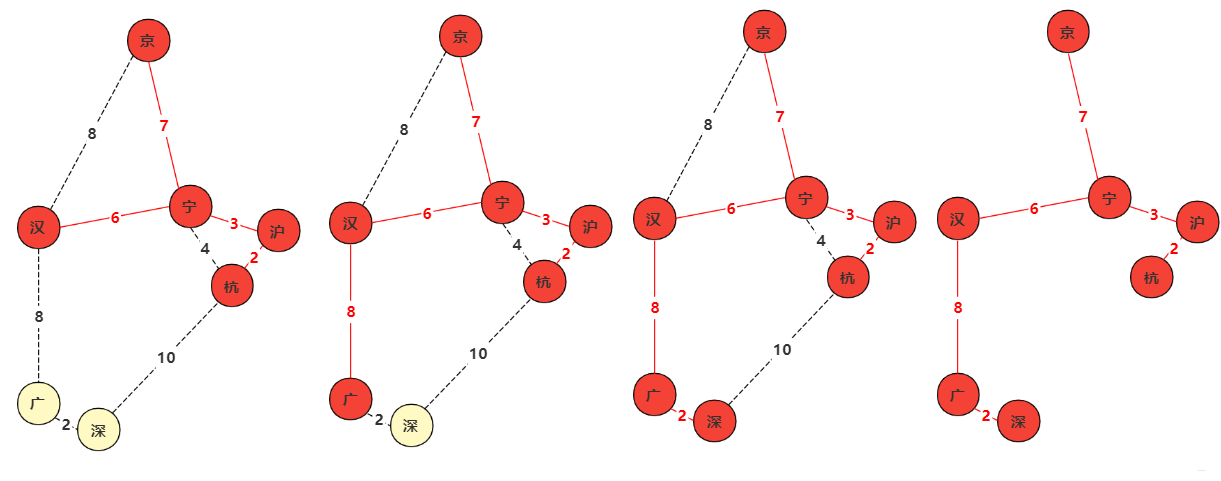
- 从集合q1找到距离最小的那个边v1并 判断边是否存在未被标记的一点p ,如果p不存在说明已经确定过那么跳过当前边处理,如果未被标(访问)记那么标记该点p,并且与p相连的未知点(未被标记)构成的边加入集合q1, 边v1(可以进行计算距离之类,该边构成最小生成树) .
- 重复1,2直到q1为空,构成最小生成树 !
例图如下

Kruskal算法
思路:先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
简而言之,
Kruskal算法进行调度的单位是边,它的信仰为:所有边能小则小,算法的实现方面要用到并查集判断两点是否在同一集合。
算法的具体步骤为:
- 将图中所有边对象(边长、两端点)依次加入集合(优先队列)q1中。初始所有点相互独立。
- 取出集合(优先队列)q1最小边,判断边的两点是否联通。
- 如果联通说明两个点已经有其它边将两点联通了,跳过,如果不连通,则使用union(并查集合并)将两个顶点合并,这条边被使用(可以储存或者计算数值)。
- 重复2,3操作直到集合(优先队列)q1为空。此时被选择的边构成最小生成树。
例图如下
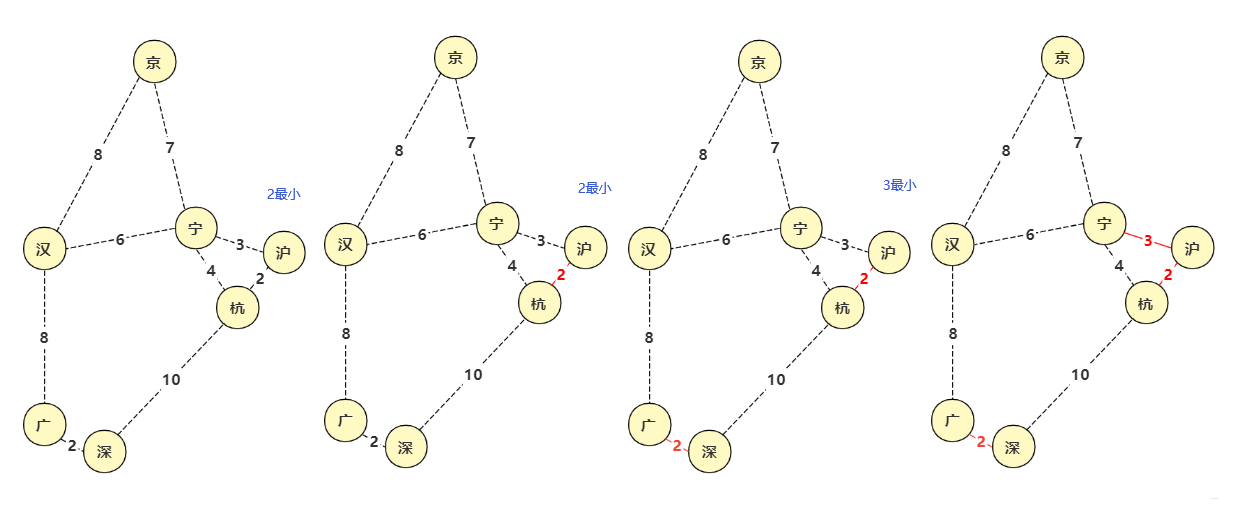
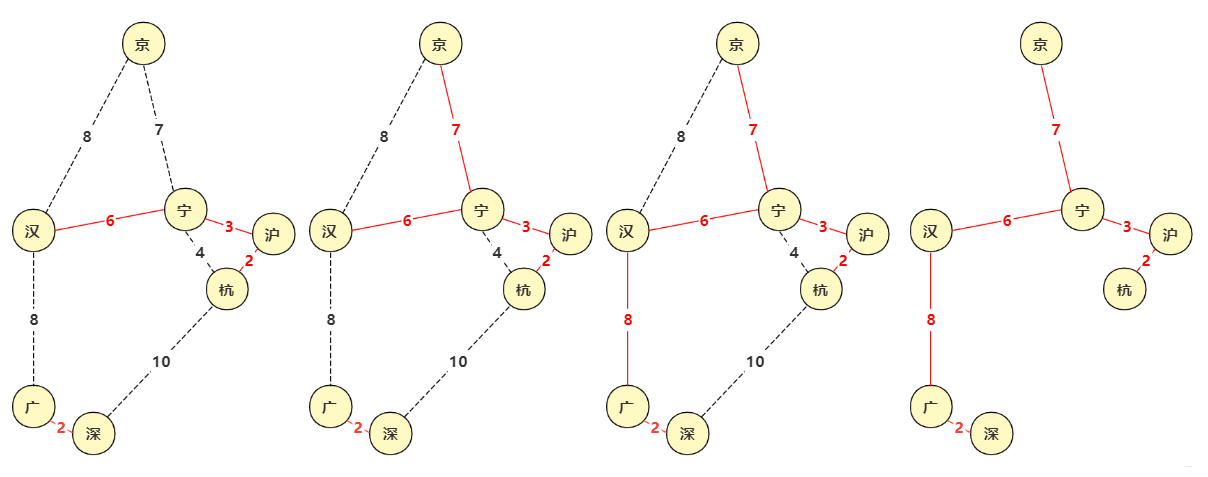
因为prim从开始到结束一直是一个整体在扩散,所以不需要考虑两棵树合并的问题,在这一点实现上稍微方便了一点。
当然,要注意的是最小生成树并不唯一,甚至同一种算法生成的最小生成树都可能有所不同,但是相同的是无论生成怎样的最小生成树:
- 能够保证所有节点连通(能够满足要求和条件)
- 能够保证所有路径之和最小(结果和目的相同)
- 最小生成树不唯一,可能多样的
最短路径
定义
从图的一个点到另一个点到路径不止一条,每条路径的长度可能不同,把路径长度最短的那条叫做最短路径。
有权图中,应该考虑各边的权值。无权图中,可以将每条边的权值看作是1。
最短路径问题可分为两方面:
- 图中一个点到其余各点的最短路径(单源点最短路径问题)
- 图中每对点之间到最短路径(所有顶点之间最短路径)
生活应用
交通网络问题:从甲地到乙地有多条通路,哪一条最短?
对于单源点最短路径问题,采用Dijkstra算法(现在路由器中路由算法有部分也采用这种方法)
对于多源路径最短问题,采用Floyd算法(其实也可以用Dijkstra算法对每个源点遍历)
最短路径的两种算法
Dijkstra算法
思路:狄克斯特拉算法解决图中一点到其余各点到最短路径的问题。其基本思想位:图G=(V,E)是一个有权有向图,把顶点V分成两组,第一组为已求出最短路径的点的集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径v,…k,就将k加入到集合S中,直到全部到点都加入S集合中,算法结束),第二组为其余未确定最短路径的点的集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入到S中。
给出一种算法可视化过程 【算法】最短路径查找—Dijkstra算法
Floyd算法
思路:Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。
从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
过程描述:
- 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
- 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
给出一种算法可视化过程 最短路径Floyd算法
还可以参考博客 图最短路径算法之弗洛伊德算法(Floyd)
代码实现
注:思路和具体的代码实现相去甚远,在图中尤为明显,一定要自己敲试试,每行代码都需要试着理解
C++实现
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
class MatrixGraph {
// dijkstra 辅助结点
class DijMatirx {
public:
bool best = false;
int distance = INT_MAX;
int before = -1;
DijMatirx() {}
};
protected:
int vexNum, edgeNum, maxVexNumb;
int** matrix;
int* elems;
bool* flag;
public:
// 初始化图大小(顶点个数)
MatrixGraph(int size) {
vexNum = 0;
edgeNum = 0;
maxVexNumb = size;
matrix = new int* [size];
for (int i = 0; i < size; i++) {
matrix[i] = new int[size];
for (int j = 0; j < size; j++) {
// if (i == j) matrix[i][j] = 0;
// else matrix[i][j] = -1;
matrix[i][j] = 0;
}
}
elems = new int[size];
flag = new bool[size];
}
// 析构
~MatrixGraph() {
delete flag;
delete elems;
delete matrix;
}
// 插入顶点
void insertVertex(int vertex) {
if (vexNum < maxVexNumb) {
elems[vexNum] = vertex;
vexNum++;
}
else cout << "顶点已满,请重新初始化图!" << endl;
}
// 插入边
void insertEdge(int v1, int v2, int weight) {
matrix[v1][v2] = weight;
matrix[v2][v1] = weight;
edgeNum++;
}
// 显示邻接矩阵
void showGraph() {
for (int i = 0; i < maxVexNumb; i++) {
for (int j = 0; j < maxVexNumb; j++) {
printf("%3d ", matrix[i][j]);
}
cout << endl;
}
}
private:
// 获取当前顶点个数
int getNumbOfVertex() {
return vexNum;
}
// 获取下标为i的顶点元素
int getValueByIndex(int i) {
return elems[i];
}
//清除访问信息
void clearIsVisited() {
for (int i = 0; i < vexNum; i++) flag[i] = false;
}
// 获取邻接结点下标
int getFirstNeighbor(int index) {
for (int j = 0; j < vexNum; j++) {
if (matrix[index][j] > 0) return j;
}
return -1;
}
// 根据前一个邻接结点下标获取下一个邻接结点
int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vexNum; j++) {
if (matrix[v1][j] > 0) return j;
}
return -1;
}
// 深度优先遍历 辅助
void depthFirstSearch(int i) {
cout << "->" << getValueByIndex(i);
flag[i] = true;
int w = getFirstNeighbor(i);
while (w != -1) {
if (!flag[w]) {
depthFirstSearch(w);
}
w = getNextNeighbor(i, w);
}
}
// 广度优先遍历 辅助
void breadthFirstSearch(int i) {
if (flag[i]) return;
cout << "->" << getValueByIndex(i);
flag[i] = true;
breadthFirstSearch(getFirstNeighbor(i));
}
// dijkstra设置最小距离
void setDistance(vector<DijMatirx*> dij, int i) {
for (int j = 0; j < vexNum; j++) {
if (matrix[i][j] > 0) {
if (!dij[j]->best) {
if (dij[j]->distance > matrix[i][j] + dij[i]->distance) {
dij[j]->distance = matrix[i][j] + dij[i]->distance;
dij[j]->before = i;
}
}
}
}
}
// 获取dij结点中distance最小的点下标
int getNextMinDistance(vector<DijMatirx*> dij) {
int temp = INT_MAX;
int goal = -1;
for (int i = 0; i < vexNum; i++) {
if (temp > dij[i]->distance && !dij[i]->best) {
temp = dij[i]->distance;
goal = i;
}
}
return goal;
}
public:
// 深度优先遍历
void depthFirstSearch() {
clearIsVisited();
cout << "DFS_开始遍历";
for (int i = 0; i < vexNum; i++) {
if (!flag[i]) depthFirstSearch(i);
}
cout << endl;
}
// 广度优先遍历
void breadthFirstSearch() {
clearIsVisited();
cout << "BFS_开始遍历";
for (int i = 0; i < vexNum; i++) {
if (!flag[i]) breadthFirstSearch(i);
}
cout << endl;
}
// prime
void prime() {
int* visitedVertex = new int[vexNum];
for (int i = 0; i < vexNum; i++) visitedVertex[i] = -1;
int** newMatrix = new int* [vexNum];
for (int i = 0; i < vexNum; i++) {
newMatrix[i] = new int[vexNum];
for (int j = 0; j < vexNum; j++) newMatrix[i][j] = 0;
}
int trueBegan = 0, began = 0, end = -1;
clearIsVisited();
visitedVertex[0] = 0;
flag[0] = true;
int weight = 0, goal = 1;
cout << "Prime算法最小生成树如下:" << endl;
while (goal < vexNum) {
int numb = INT_MAX;
for (int i = 0; i < vexNum; i++) {
if (visitedVertex[i] == -1) break;
began = visitedVertex[i];
for (int j = 0; j < vexNum; j++) {
if (matrix[began][j] > 0 && numb > matrix[began][j] && !flag[j]) {
numb = matrix[began][j];
end = j;
trueBegan = began;
}
}
}
visitedVertex[goal] = end;
flag[end] = true;
weight += matrix[trueBegan][end];
newMatrix[trueBegan][end] = matrix[trueBegan][end];
goal++;
}
cout << "权重为:" << weight << endl;
for (int i = 0; i < maxVexNumb; i++) {
for (int j = 0; j < maxVexNumb; j++) {
printf("%3d ", newMatrix[i][j]);
}
cout << endl;
}
}
// dijkstra
void dijkstra(int began, int end) {
cout << "dijkstra:" << began << "至" << end << "最短路径如下:" << endl;
vector<DijMatirx*> dij;
for (int i = 0; i < vexNum; i++) {
DijMatirx* item = new DijMatirx();
dij.push_back(item);
}
dij[began]->distance = 0;
for (int i = 0, item = began; i < vexNum; i++) {
setDistance(dij, item);
dij[item]->best = true;
item = getNextMinDistance(dij);
}
stack<int> stack;
int temp = end;
while (temp != began) {
stack.push(elems[temp - 1]);
temp = dij[temp]->before;
}
cout << elems[began];
while (!stack.empty()) {
cout << " ->" << elems[stack.top()];
stack.pop();
}
cout << endl;
for (int i = 0; i < vexNum; i++) {
DijMatirx* temp = dij.back();
delete temp;
dij.pop_back();
}
}
};
int main() {
MatrixGraph* graph = new MatrixGraph(8);
for (int i = 1; i < 9; i++) graph->insertVertex(i);
graph->insertEdge(0, 1, 1);
graph->insertEdge(0, 2, 2);
graph->insertEdge(1, 3, 4);
graph->insertEdge(1, 4, 3);
graph->insertEdge(2, 5, 1);
graph->insertEdge(2, 6, 4);
graph->insertEdge(3, 7, 2);
graph->insertEdge(4, 7, 5);
graph->insertEdge(5, 6, 2);
graph->showGraph();
graph->depthFirstSearch();
graph->breadthFirstSearch();
graph->dijkstra(0, 6);
graph->dijkstra(0, 7);
graph->prime();
return 0;
}
Java实现
邻接矩阵
package com.drizzledrop.Graph;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Stack;
public class MatrixGraph {
// 存储顶点集合
private ArrayList<String> vertexList;
// 存储图对应的邻接矩阵
private int[][] edges;
// 总边数
private int numOfEdges;
// 某个结点是否被访问过
private boolean[] isVisited;
// 构造器,进行初始化
public MatrixGraph(int vertexSize) {
edges = new int[vertexSize][vertexSize];
vertexList = new ArrayList<>(vertexSize);
}
// 添加顶点/结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
/**
* 添加边
*
* @param v1 第一个顶点的下标
* @param v2 第二个顶点的下标
* @param weight 权值
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
// 显示图的对应矩阵
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
/**
* 以下是深度优先搜索和广度优先搜索需要用到的基础方法
* 得到第一个临接结点的下标
*
* @param index 第几个结点
* @return 存在则返回下标,否则返回-1
*/
private int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0) {
return j;
}
}
return -1;
}
/**
* 根据前一个邻接结点的下标来获取从下一个邻接结点
*
* @param v1 要查找的结点的下标
* @param v2 开始的下标
* @return 存在则返回下标,否则返回-1
*/
private int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) {
return j;
}
}
return -1;
}
// 获取返回结点个数
private int getNumOfVertex() {
return vertexList.size();
}
// 获取边的数量
private int getNumOfEdges() {
return numOfEdges;
}
// 获取结点i(下标)的值
private String getValueByIndex(int i) {
return vertexList.get(i);
}
// 返回v1 和 v2 的权值
private int getWeight(int v1, int v2) {
return edges[v1][v2];
}
// 清除访问信息
private void clearIsVisited() {
isVisited = new boolean[vertexList.size()];
for (int i = 0; i < isVisited.length; i++) isVisited[i] = false;
}
// 深度优先遍历算法——辅助
private void depthFirstSearch(int i) {
//输出当前结点
System.out.print("->" + getValueByIndex(i));
//将结点设置为已访问
isVisited[i] = true;
//查找结点i 的第一个邻接结点 w
int w = getFirstNeighbor(i);
while (w != -1) {
if (!isVisited[w]) {
depthFirstSearch(w);
}
w = getNextNeighbor(i, w);
}
}
// 深度优先遍历算法
public void depthFirstSearch() {
clearIsVisited();
System.out.print("开始遍历");
//遍历所有节点
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
depthFirstSearch(i);
}
}
System.out.println();
}
// 广度优先算法——辅助
private void breadthFirstSearch(int i) {
//队列头结点的下标
int headIndex;
//邻接节点
int neighborIndex;
//记录节点访问的顺序
LinkedList queue = new LinkedList();
//输出结点信息
System.out.print("->" + getValueByIndex(i));
//标记已访问
isVisited[i] = true;
//将结点加入队列
queue.addLast(i);
while (!queue.isEmpty()) {
//取出队列的头结点下标
headIndex = (Integer) queue.removeFirst();
//得到第一个邻接结点的下标
neighborIndex = getFirstNeighbor(headIndex);
//不断进入下一层
while (neighborIndex != -1) {
//判断是否访问过
if (!isVisited[neighborIndex]) {
System.out.print("->" + getValueByIndex(neighborIndex));
//标记已访问
isVisited[neighborIndex] = true;
//将结点加入队列
queue.addLast(neighborIndex);
}
neighborIndex = getNextNeighbor(headIndex, neighborIndex);
}
}
}
// 广度优先遍历算法
public void breadthFirstSearch() {
clearIsVisited();
System.out.print("开始遍历");
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
breadthFirstSearch(i);
}
}
System.out.println();
}
// floyd
public void Floyd(int began, int end) {
int size = vertexList.size();
int[][] graph = new int[size][size];
int[][] path = new int[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
path[i][j] = -1;
if (i == j) graph[i][i] = 0;
else {
graph[i][j] = edges[i][j] > 0 ? edges[i][j] : 65535;
}
}
}
for (int v = 0; v < size; v++) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (graph[i][j] > graph[i][v] + graph[v][j]) {
graph[i][j] = graph[i][v] + graph[v][j];
path[i][j] = v;
}
}
}
}
System.out.println("各点最短路径如下:");
for (int[] array : graph) {
System.out.println(Arrays.toString(array));
}
System.out.println("其中" + began + "至" + end + "最短路线如下:");
Stack<Integer> stack = new Stack<>();
stack.push(end);
int goal = path[began][end];
while (goal != -1) {
stack.push(goal);
goal = path[began][goal];
}
System.out.print(began);
while (!stack.isEmpty()) {
System.out.print("->" + stack.pop());
}
System.out.println();
}
// 获取非值数目
private int[] isVisitedNumb(boolean[] isVisited) {
int numb = 0;
for (boolean b : isVisited) {
if (b) numb++;
}
int[] numbArray = new int[numb];
int j = 0;
for (int i = 0; i < isVisited.length; i++) {
if (isVisited[i]) numbArray[j++] = i;
}
return numbArray;
}
// prime算法辅助
private int setPrimeNumb(int[][] graph, boolean[] isVisited) {
int weight = 0;
for (int i = 0; i < isVisited.length; i++) {
int id = 0;
int temp = 65535;
int answer = 0;
int[] numb = isVisitedNumb(isVisited);
for (int value : numb) {
for (int j = 0; j < isVisited.length; j++) {
if (edges[value][j] != 0 && edges[value][j] < temp && !isVisited[j]) {
id = j;
temp = edges[value][j];
answer = value;
}
}
}
graph[answer][id] = edges[answer][id];
weight += graph[answer][id];
isVisited[id] = true;
}
return weight;
}
// Prime算法
public void Prime() {
int size = vertexList.size();
boolean[] isVisited = new boolean[size];
int[][] graph = new int[size][size];
int goal = 0;
isVisited[goal] = true;
System.out.println("最小生成树权重为:" + setPrimeNumb(graph, isVisited));
for (int[] link : graph) {
System.out.println(Arrays.toString(link));
}
}
}
package com.drizzledrop.Graph;
public class TestMatrixGraph {
public static void main(String[] args) {
// 创建结点
String []Vertex = {"1", "2", "3", "4", "5", "6", "7", "8"};
MatrixGraph graph = new MatrixGraph(Vertex.length);
// 添加结点
for(String vertex : Vertex){
graph.insertVertex(vertex);
}
// 添加边
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 2);
graph.insertEdge(1, 3, 4);
graph.insertEdge(1, 4, 3);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 4);
graph.insertEdge(3, 7, 2);
graph.insertEdge(4, 7, 5);
graph.insertEdge(5, 6, 2);
// 显示邻接矩阵
graph.showGraph();
// 深度优先遍历
graph.depthFirstSearch();
// 广度优先遍历
graph.breadthFirstSearch();
// Floyd 最短路径
graph.Floyd(0, 6);
graph.Floyd(0,7);
// Prime 最小生成树
graph.Prime();
}
}
邻接表
package com.drizzledrop.Graph;
import java.util.ArrayList;
import java.util.Stack;
public class ListGraph {
// 边节点
private class ENode {
int indexVertex;
int weight;
ENode nextENode;
public ENode(int index, int weight, ENode next) {
indexVertex = index;
this.weight = weight;
nextENode = next;
}
}
// 顶点节点
private class VNode {
String data;
ENode firstENode;
public VNode(String str, ENode fNode) {
data = str;
firstENode = fNode;
}
}
// dijkstra节点
private class DjNode {
VNode dVNode;
int max = 65535;
int prve = -1;
boolean isMin = false;
public DjNode(VNode node){
dVNode = node;
}
}
// 顶点数组
private ArrayList<VNode> Vertex;
// 顶点总数
private int vertexNumb = 0;
// 某个结点是否被访问过
private boolean[] isVisited;
// 顶点初始化
public ListGraph(String[] vertex) {
Vertex = new ArrayList<>(vertex.length);
for (int i = 0; i < vertex.length; i++) {
Vertex.add(new VNode(vertex[i], null));
vertexNumb++;
}
}
// 添加顶点
public void insertVertex(String vertex) {
Vertex.add(new VNode(vertex, null));
vertexNumb++;
}
// 添加边
public boolean insertEdge(int v1, int v2, int weight) {
ENode temp = Vertex.get(v1).firstENode;
if (temp == null) {
Vertex.get(v1).firstENode = new ENode(v2, weight, null);
return true;
}
ENode tempBefore = temp;
while (temp != null) {
if (temp.indexVertex == v2) return false;
tempBefore = temp;
temp = temp.nextENode;
}
tempBefore.nextENode = new ENode(v2, weight, null);
return true;
}
// 显示顶点的边信息
public void showGraph() {
for (VNode v : Vertex) {
System.out.print(v.data + ":");
if (v.firstENode != null) {
ENode temp = v.firstENode;
while (temp != null) {
int tempInt = temp.indexVertex + 1;
System.out.print("->" + tempInt + ("(权重为 ") + temp.weight + ")");
temp = temp.nextENode;
}
}
System.out.println();
}
}
// 获取边结点 顶点信息
public int getIndexVertex(ENode node) {
return node.indexVertex;
}
// 清除访问信息
private void clearIsVisited() {
isVisited = new boolean[vertexNumb];
for (int i = 0; i < isVisited.length; i++) isVisited[i] = false;
}
// 深度优先遍历——辅助
private void depthFirstSearch(int i) {
System.out.print("->" + Vertex.get(i).data);
isVisited[i] = true;
ENode temp = Vertex.get(i).firstENode;
while (temp != null) {
int item = getIndexVertex(temp);
if (!isVisited[item]) {
depthFirstSearch(item);
}
temp = temp.nextENode;
}
}
// 深度优先遍历
public void depthFirstSearch() {
clearIsVisited();
System.out.print("开始遍历");
for (int i = 0; i < vertexNumb; i++) {
if (!isVisited[i])
depthFirstSearch(i);
}
System.out.println();
}
// 广度优先遍历——辅助
private void breadthFirstSearch(int i) {
if (!isVisited[i]) {
System.out.print("->" + Vertex.get(i).data);
isVisited[i] = true;
} else {
ENode temp = Vertex.get(i).firstENode;
while (temp != null) {
int item = getIndexVertex(temp);
if (!isVisited[item]) {
System.out.print("->" + Vertex.get(item).data);
isVisited[item] = true;
}
temp = temp.nextENode;
}
}
}
// 广度优先遍历
public void breadthFirstSearch() {
clearIsVisited();
System.out.print("开始遍历");
// 遍历所有顶点
for (int i = 0; i < vertexNumb; i++) {
breadthFirstSearch(i);
}
System.out.println();
}
// 辅助获取未标记中离源点最近的点
private int getMinMax(DjNode[] dij) {
int min = 65535;
int goal = -1;
for (int i = 0; i < dij.length; i++) {
if (dij[i].max < min && !dij[i].isMin) {
min = dij[i].max;
goal = i;
}
}
return goal;
}
// dijkstra 辅助
private void Dijkstra(int prve, DjNode[] dij) {
ENode node = dij[prve].dVNode.firstENode;
while (node != null) {
int id = node.indexVertex;
if (dij[id].max > dij[prve].max + node.weight) {
dij[id].prve = prve;
dij[id].max = dij[prve].max + node.weight;
}
node = node.nextENode;
}
}
// dijkstra
public void Dijkstra(int start, int goal) {
DjNode[] dij = new DjNode[vertexNumb];
for (int i = 0; i < vertexNumb; i++) {
dij[i] = new DjNode(Vertex.get(i));
}
dij[start].isMin = true;
dij[start].max = 0;
dij[start].prve = 0;
Dijkstra(start, dij);
int temp = getMinMax(dij);
while (temp != -1) {
dij[temp].isMin = true;
Dijkstra(temp, dij);
temp = getMinMax(dij);
}
Stack<Integer> stack = new Stack<>();
stack.push(goal);
while (goal != start) {
stack.push(dij[goal].prve);
goal = dij[goal].prve;
}
System.out.print("最短路径为");
while(!stack.isEmpty()){
System.out.print("->" + dij[(stack.pop())].dVNode.data);
}
System.out.println();
}
}
package com.drizzledrop.Graph;
public class TestListVertex {
public static void main(String[] args) {
// 创建结点
String[] Vertex = {"1", "2", "3", "4", "5", "6", "7", "8"};
ListGraph graph = new ListGraph(Vertex);
// 添加边
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 2);
graph.insertEdge(1, 3, 4);
graph.insertEdge(1, 4, 3);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 4);
graph.insertEdge(3, 7, 2);
graph.insertEdge(4, 7, 5);
graph.insertEdge(5, 6, 2);
// 显示邻接表
graph.showGraph();
// 深度优先遍历
graph.depthFirstSearch();
// 广度优先遍历
graph.breadthFirstSearch();
// dijkstra 最短路径
graph.Dijkstra(0, 6); // 1到7最优:1->3->6->7
graph.Dijkstra(0, 7); // 1到8最优:1->2->4->8
}
}
从两种存储结构代码可知,深度优先遍历都用到了递归实现,而广度优先遍历有队列的思想在里面,而由于邻接表的实现方式,邻接表在广度优先遍历上更容易
Kruskal算法
为什么把Kruskal算法单列出来呢...因为前面用自己写的领接矩阵或者邻接表想过去实现,但发现要排序了,这样的结构做排序,先遍历读入一次,排序一次,再遍历一次获取或者核对边的头尾,直接给我整懵了,特别是前面在邻接矩阵里面写Prime算法,差点给我写出四层循环了(过于离谱,当时都不想丢进来),这个时候才真正体会到好的数据结构在算法应用上的作用(指写出四层循环时已经不想再优化的心情)
package com.drizzledrop.Graph;
public class Kruskal {
private int edgNum; //边的个数
private char[] vertexs; //顶点数组
private int[][] martix; //邻接矩阵
//使用INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//克鲁斯卡尔算法的邻接矩阵
int[][] matrix = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ {0, 12, INF, INF, INF, 16, 14},
/*B*/ {12, 0, 10, INF, INF, 7, INF},
/*C*/ {INF, 10, 0, 3, 5, 6, INF},
/*D*/ {INF, INF, 3, 0, 4, INF, INF},
/*E*/ {INF, INF, 5, 4, 0, 2, 8},
/*F*/ {16, 7, 6, INF, 2, 0, 9},
/*G*/ {14, INF, INF, INF, 8, 9, 0}};
//创建KruskalCase 对象实例
Kruskal kruskal = new Kruskal(vertexs, matrix);
//输出构建的
kruskal.showMartix();
/*EData[] edges = kruskalCase.getEdges();
System.out.println("未排序:" + Arrays.toString(edges));
kruskalCase.sortEdges(edges);
System.out.println("已排序:" + Arrays.toString(edges));*/
kruskal.kruskal();
}
//构造器
public Kruskal(char[] vertexs, int[][] martix) {
//初始化结点的个数
int vlen = vertexs.length;
//初始化顶点,复制的方式
this.vertexs = new char[vlen];
for (int i = 0; i < vlen; i++) {
this.vertexs[i] = vertexs[i];
}
//初始化边
this.martix = new int[vlen][vlen];
for (int i = 0; i < vlen; i++) {
for (int j = 0; j < vlen; j++) {
this.martix[i][j] = martix[i][j];
}
}
//统计边数
for (int i = 0; i < vlen; i++) {
for (int j = i + 1; j < vlen; j++) {
if (martix[i][j] != INF) {
edgNum++;
}
}
}
}
public void kruskal() {
//用于保存"已有最小生成树"中每个顶点在最小生成树中的终点
//如果一条边没有加入最小生成树则它的两个顶点的终点就是自身,用0表示
int[] ends = new int[edgNum];
//结果数组的索引,用于将某条符合条件的边加入结果数组
int index = 0;
EData[] res = new EData[edgNum];
//获取图中所有的边
EData[] edges = getEdges(); //共12条边
//将所有的边按照权值从小到大进行排序
sortEdges(edges);
//遍历edges数组,将符合条件的边添加到最小生成树中,如果准备加入的边没有形成回路则加入最小生成树,否则判断下一条边
for (int i = 0; i < edgNum; i++) {
//得到第i条边的顶点
int p1 = getPosition(edges[i].start); //该边的起点
int p2 = getPosition(edges[i].end); //该边的终点
//获取p1 和p2 在已有最小生成树中的终点
int m = getEnd(ends, p1);
int n = getEnd(ends, p2);
//判断是否构成回路
if (m != n) { //没有构成回路
ends[m] = n; //设置m在最小生成树中的终点
res[index++] = edges[i];//将该没有构成回路的边加入res中
}
}
System.out.println("最小生成树为:");
//<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
for (int i = 0; i < index; i++) {
System.out.println(res[i]);
}
}
//打印邻接矩阵
public void showMartix() {
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
System.out.printf("%-12d", martix[i][j]);
}
System.out.println();
}
}
/**
* 对边进行排序(冒泡排序)
*
* @param edges 边的集合
*/
public void sortEdges(EData[] edges) {
for (int i = 0; i < edges.length - 1; i++) {
for (int j = 0; j < edges.length - i - 1; j++) {
if (edges[j].weight > edges[j + 1].weight) {
EData temp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = temp;
}
}
}
}
/**
* 获取ch对应的下标
*
* @param ch
* @return
*/
public int getPosition(char ch) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == ch) { //找到了
return i;
}
}
//没有找到
return -1;
}
//获取图中的所有边
public EData[] getEdges() {
int index = 0;
EData[] edges = new EData[edgNum];
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
if (martix[i][j] != INF) {
edges[index++] = new EData(vertexs[i], vertexs[j], martix[i][j]);
}
}
}
return edges;
}
/**
* 获取下标为i顶点的终点,用于后面判断两个顶点的终点是否相同,最开始的是够ends[]都为0,则结点的中点就是本身
*
* @param ends 记录了各个顶点对应的终点是哪个,这个是在遍历过程中动态生成的
* @param i 顶点对应的下标
* @return 下标为i的顶点对应的终点的下标
*/
public int getEnd(int ends[], int i) {
//下面这个while循环,很重要
// 在本例中第三步,最小生成树中加入了<D,E>这条边,但是顶点C对应的终点还是D
// 在第四步加入<B,F>之前,会判断<C,E>这条边能否加入该最小生成树(不能加入,因为会构成回路),
// 该循环就能够让在判断<C,E>能否加入最小生成树时让顶点C对应的终点变为F,不懂在DEBUG下
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
}
//创建一个类EData,用于表示一条边(包括两个顶点和一个权值)
class EData {
char start; //一天边的起始点
char end; //一条边的终点
int weight; // 该条边的权值
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">= " + weight + "]";
}
}
搜索
树表的查找


二叉排序树
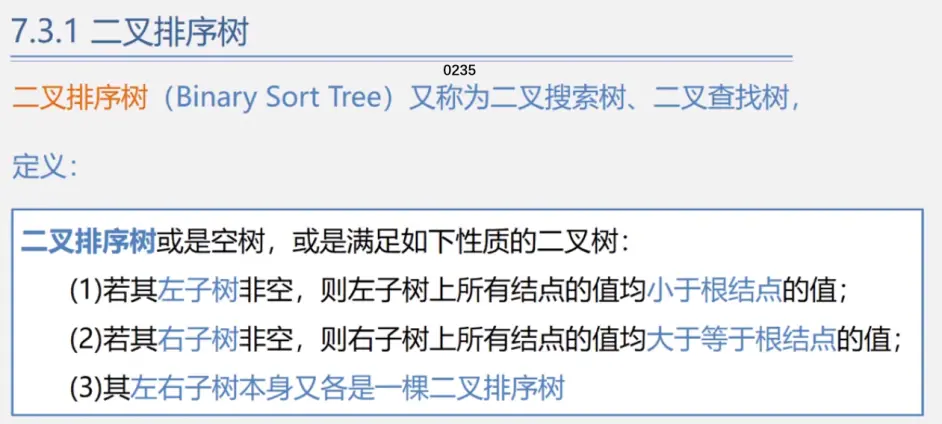
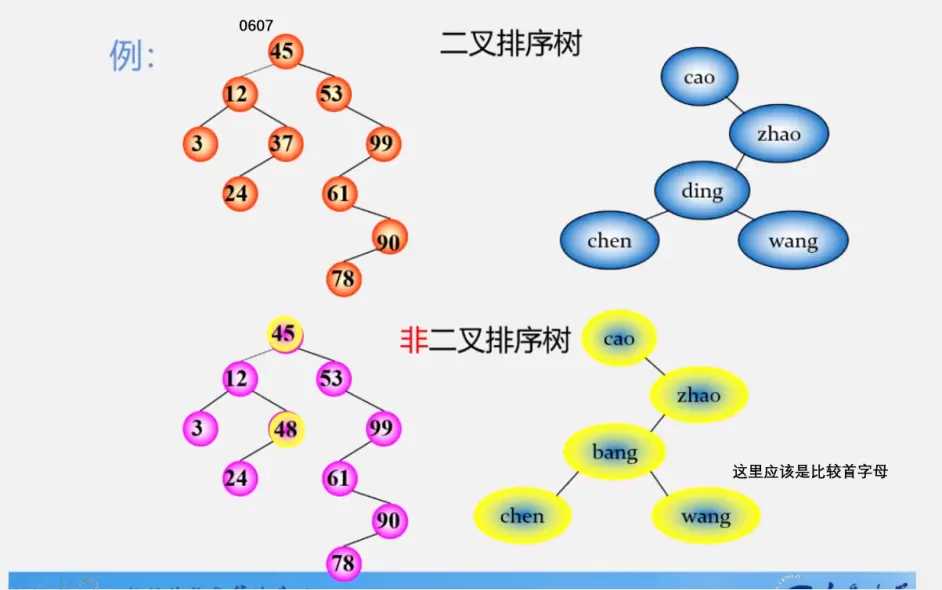
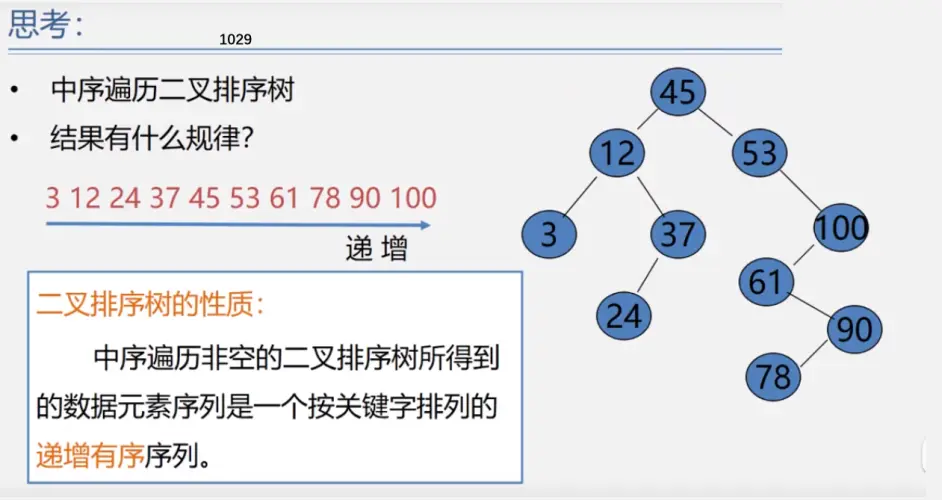
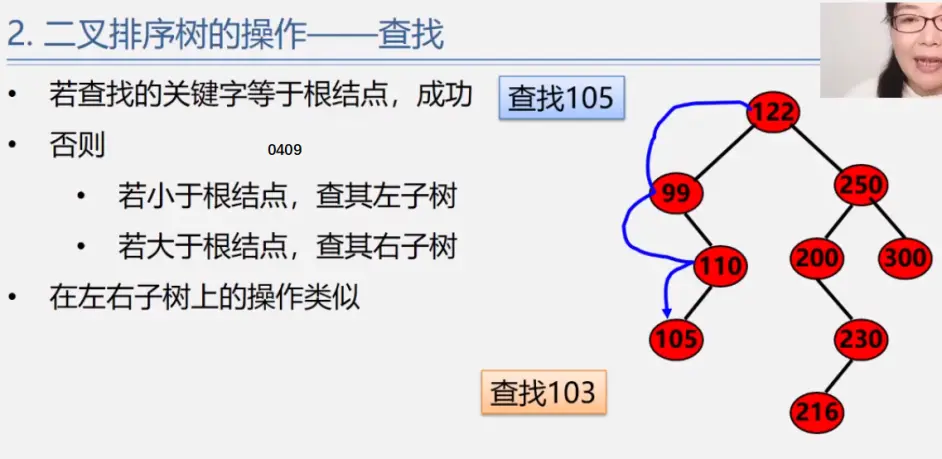

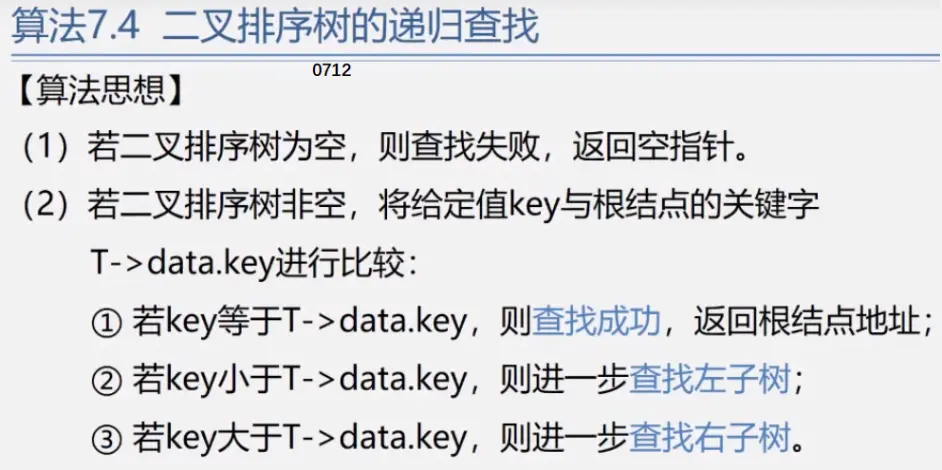


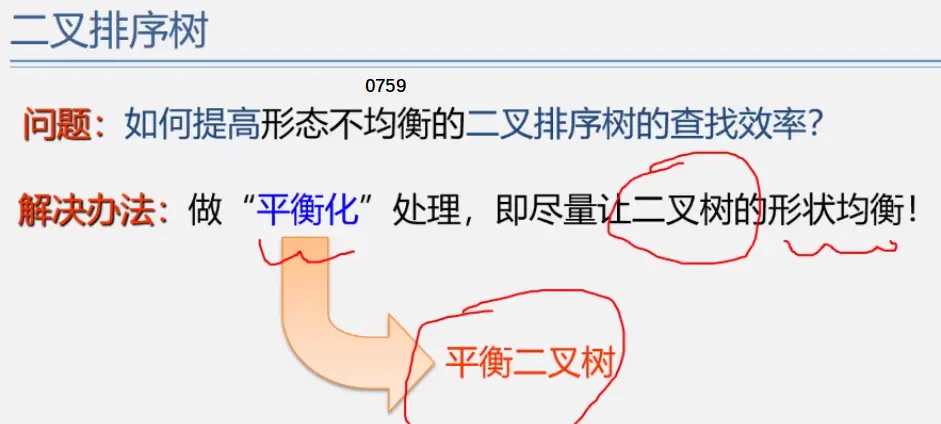
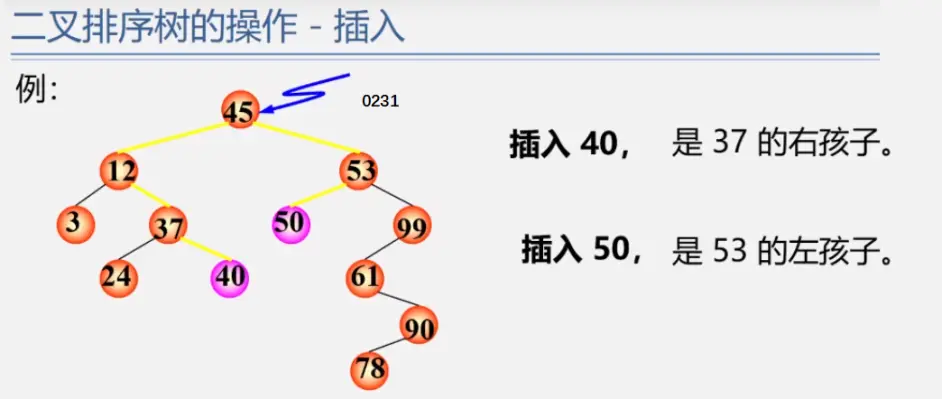


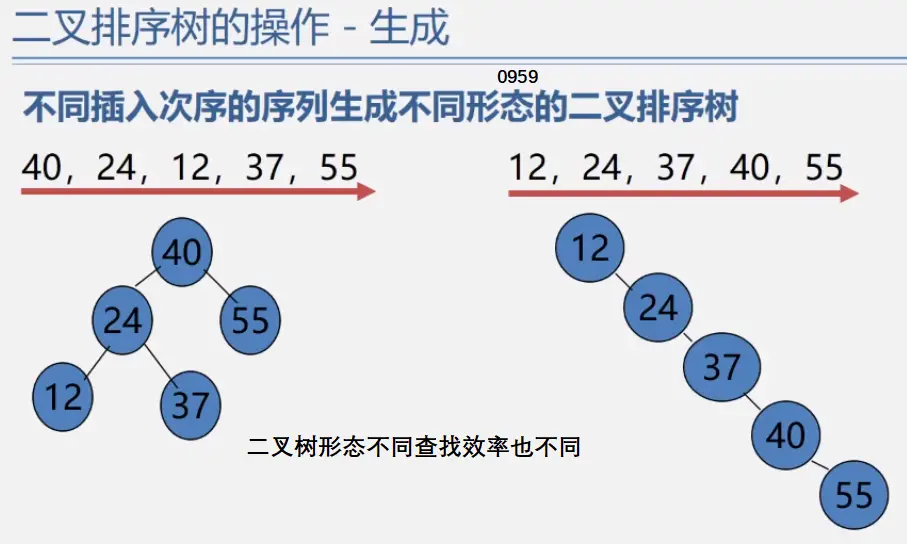
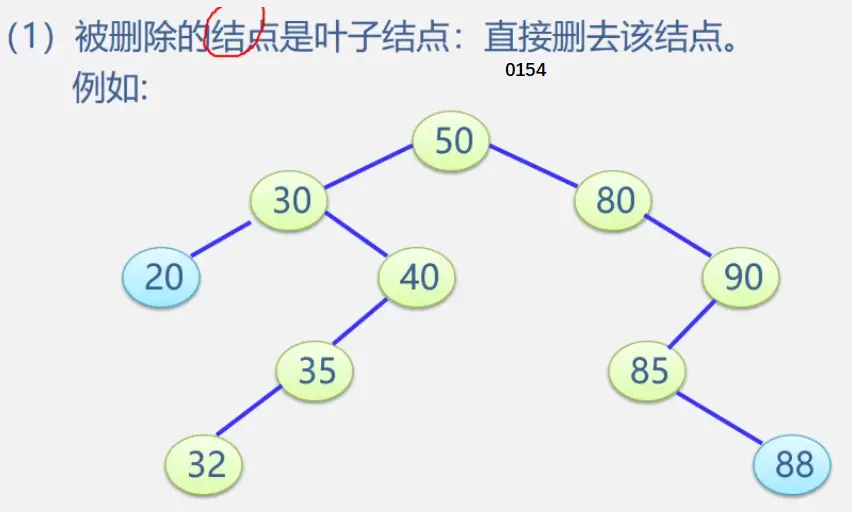
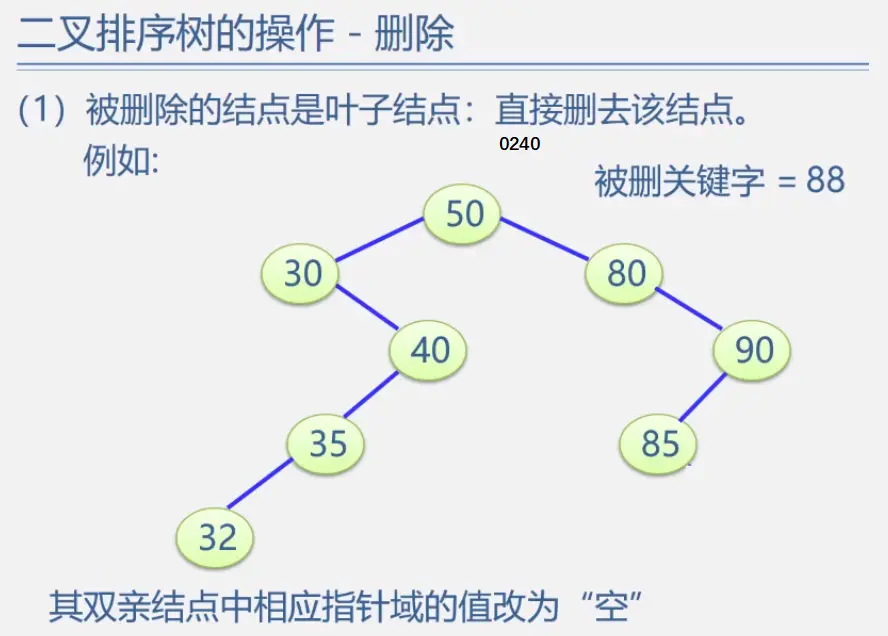
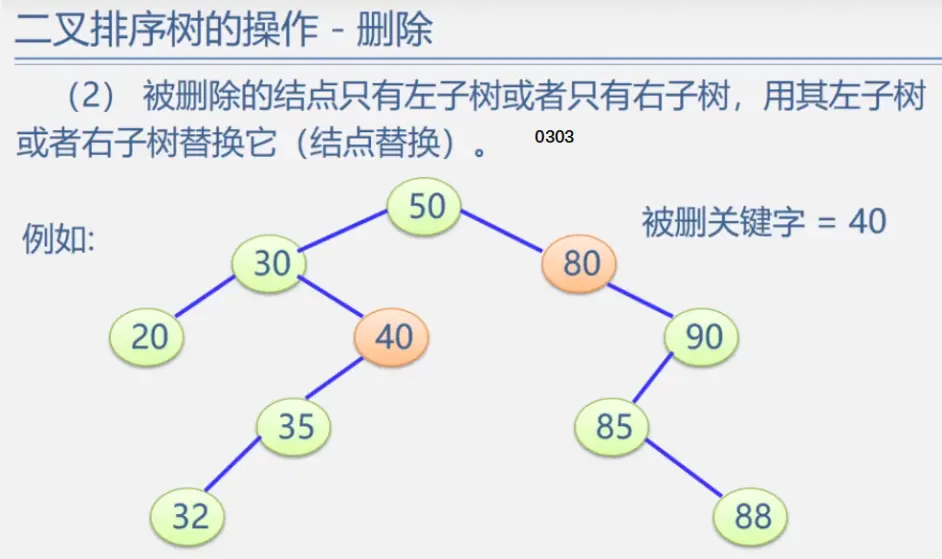
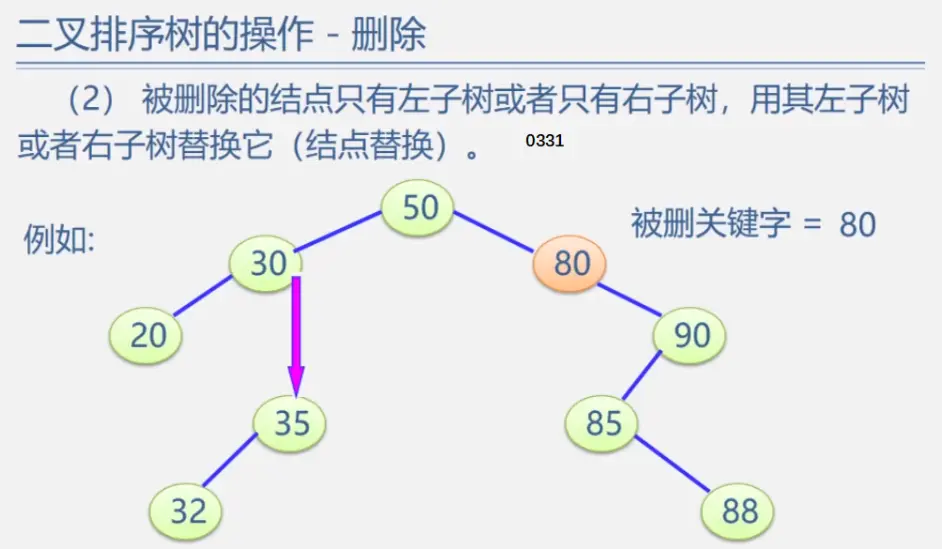
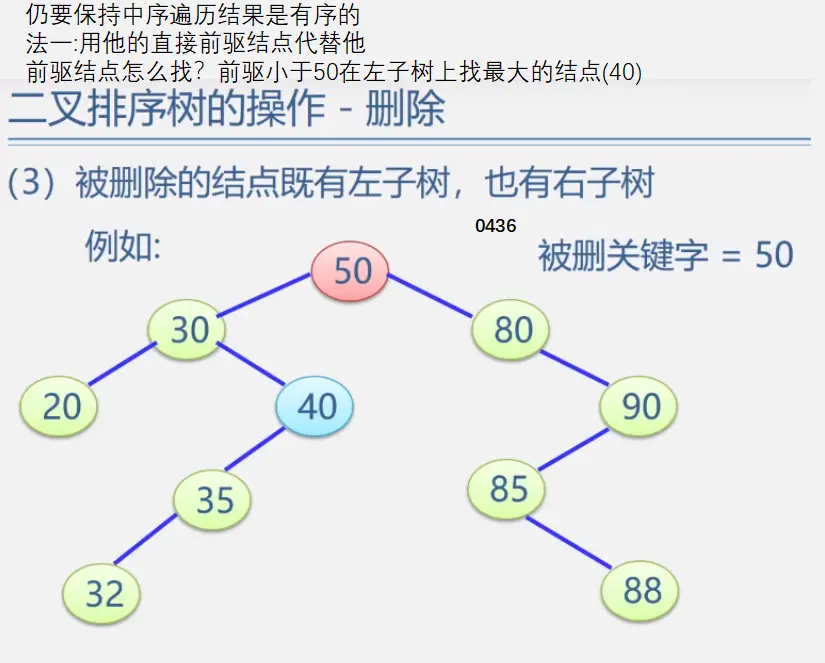
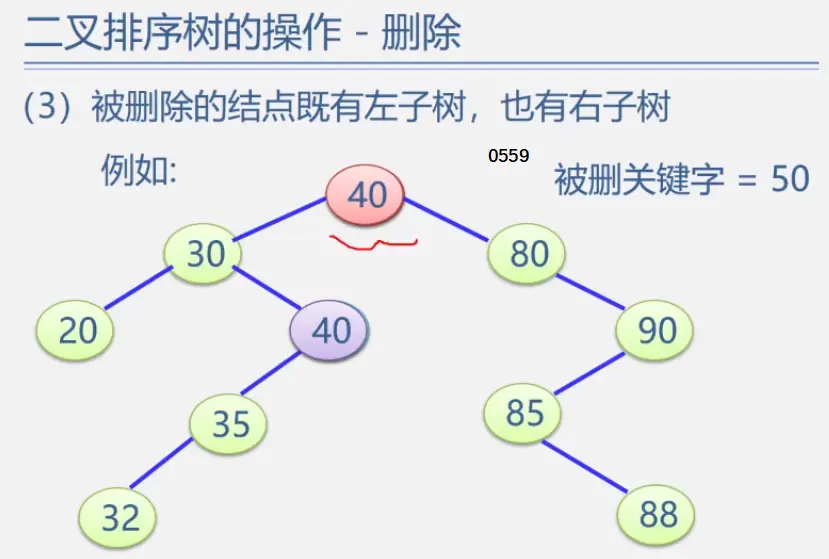
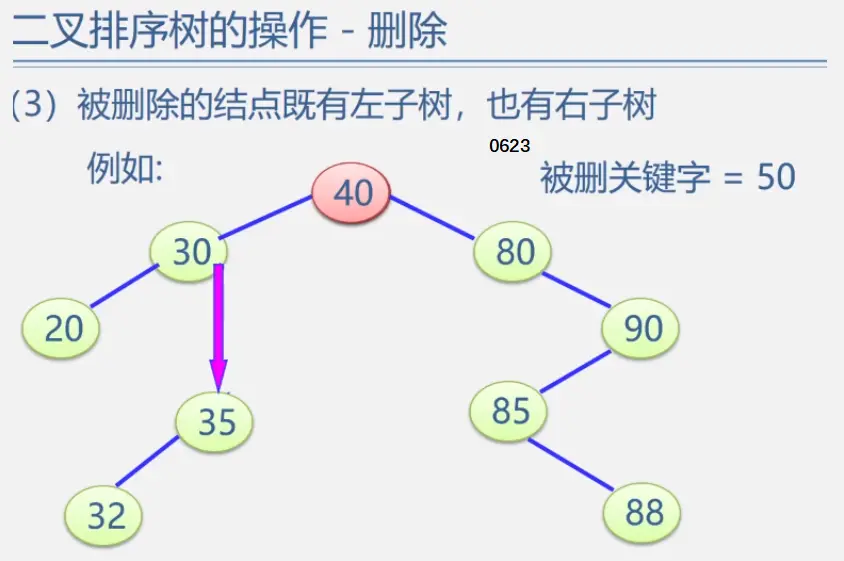
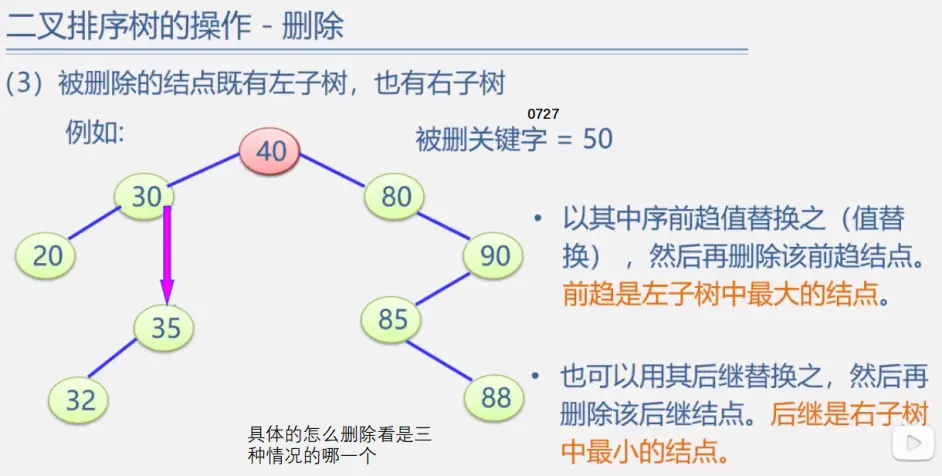
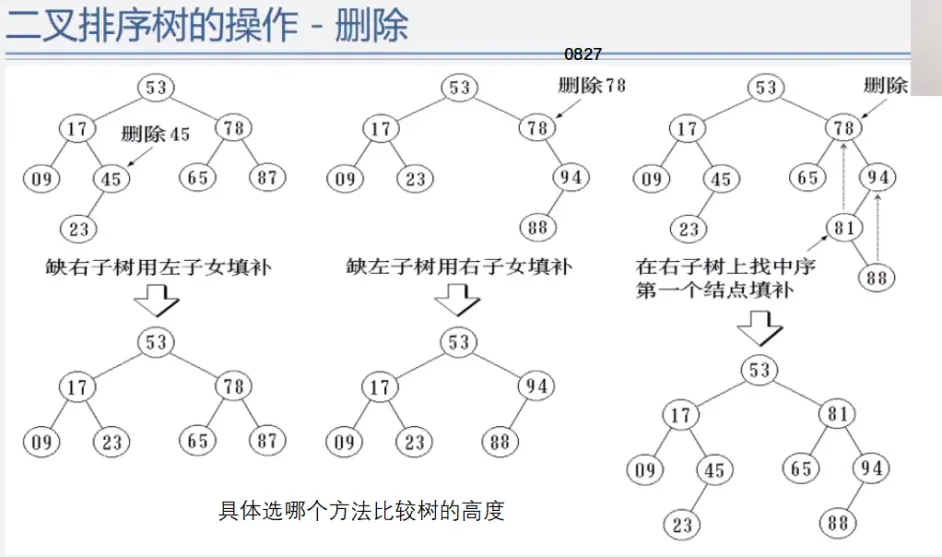

平衡二叉树


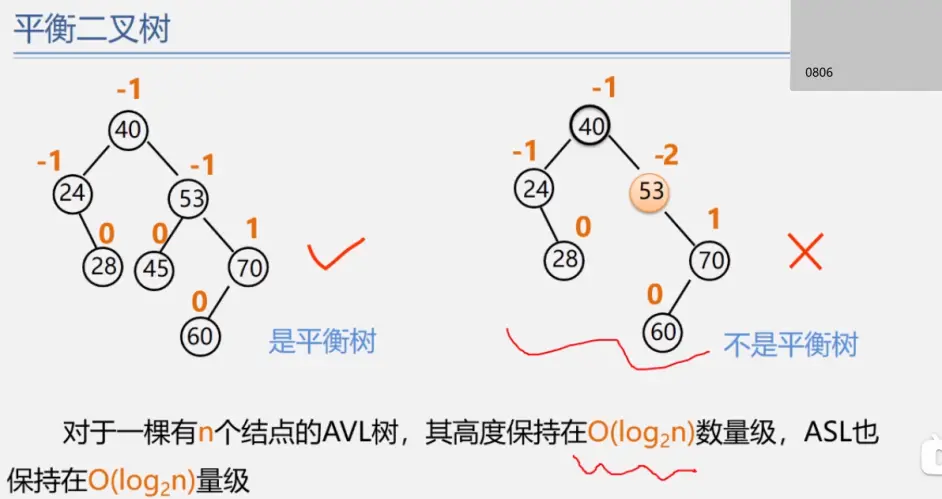
平衡二叉树的调整方法
平衡调整方法1
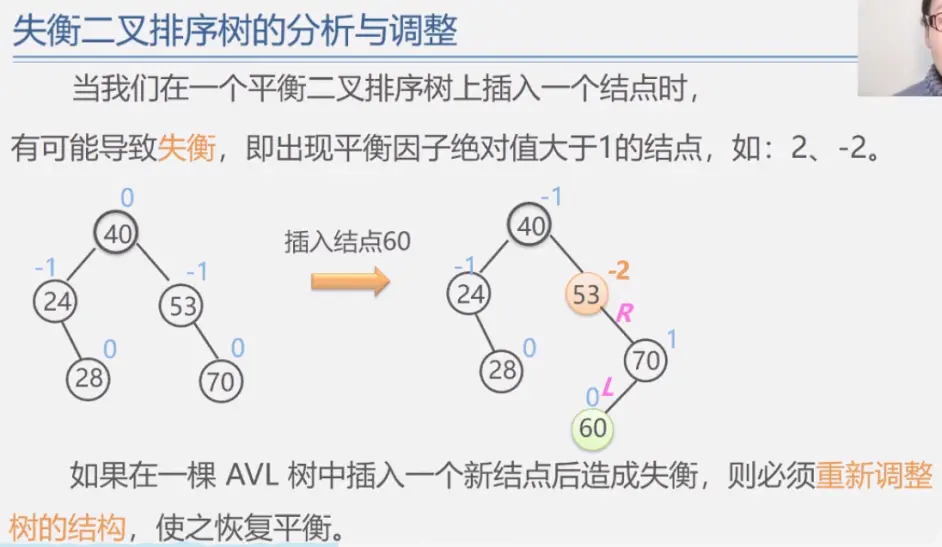
-
60比根结点大 插入到右子树 60比53大 插入到右子树 60比70小 插入其左子树
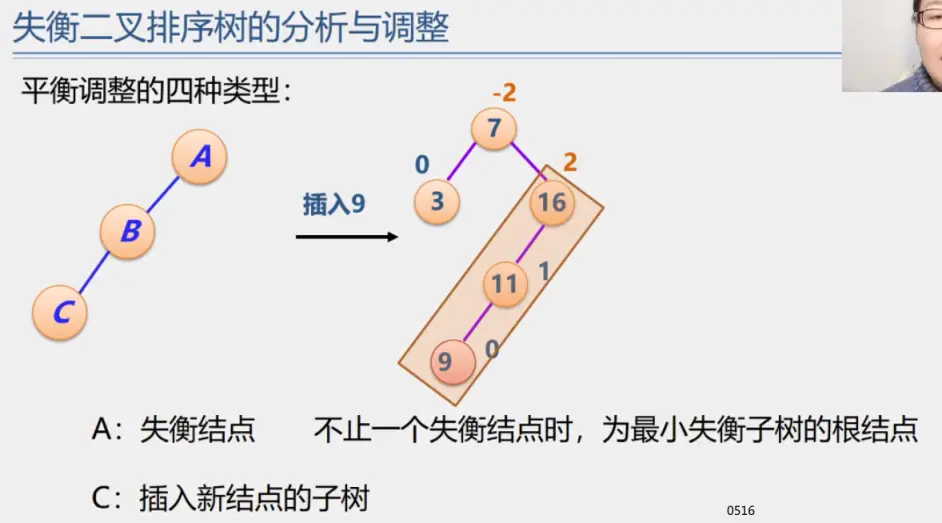
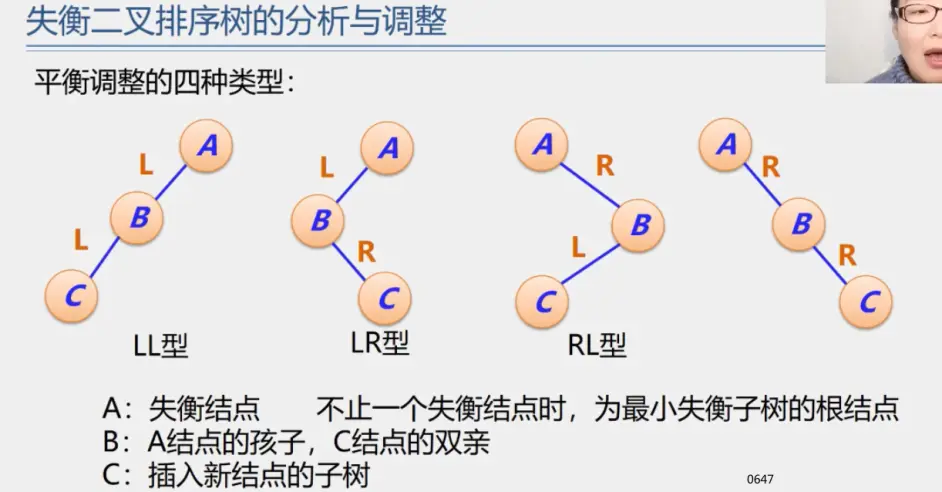
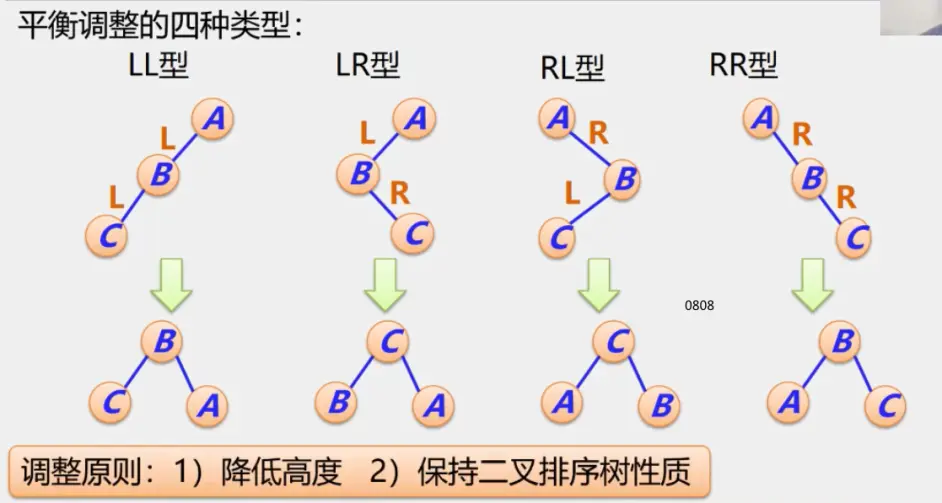
性质:左子树<根节点<右子树
所谓:找老二...
调整方法2
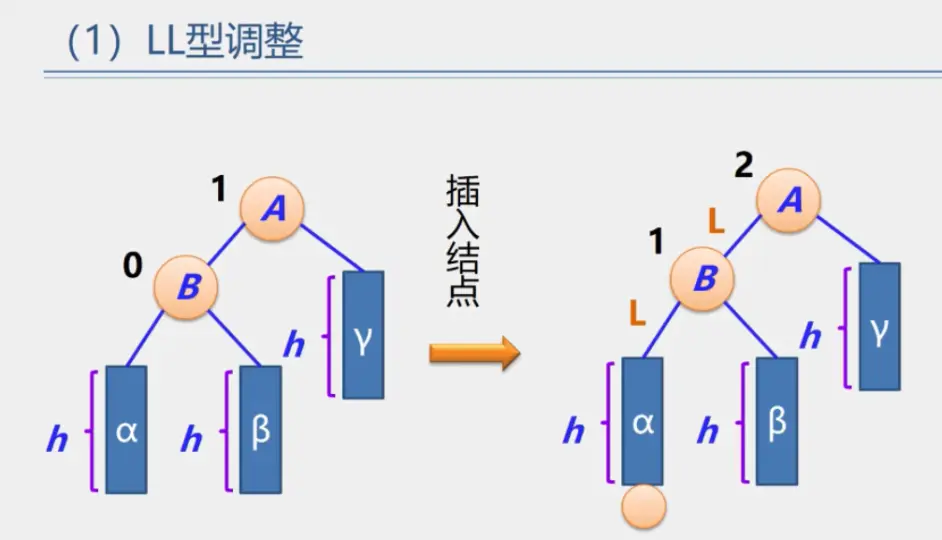
- LL型删除的结点在左子树的左子树上
- (把A转下来 平衡旋转)
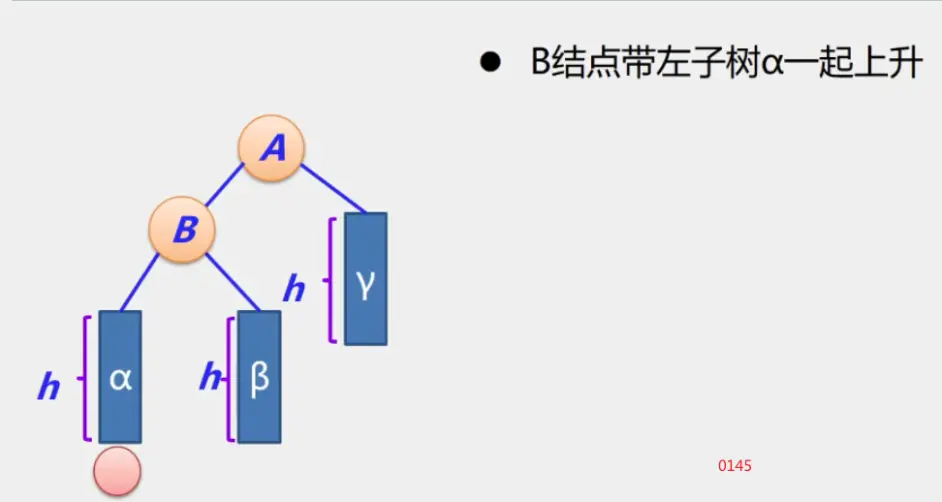
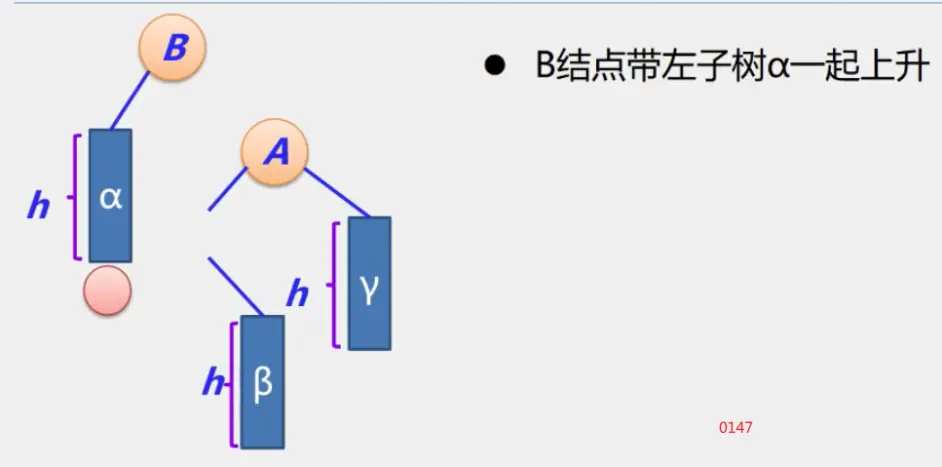
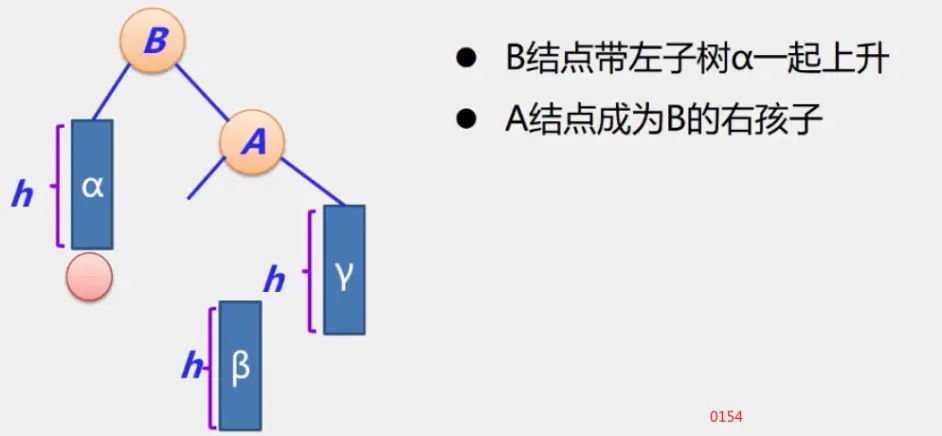

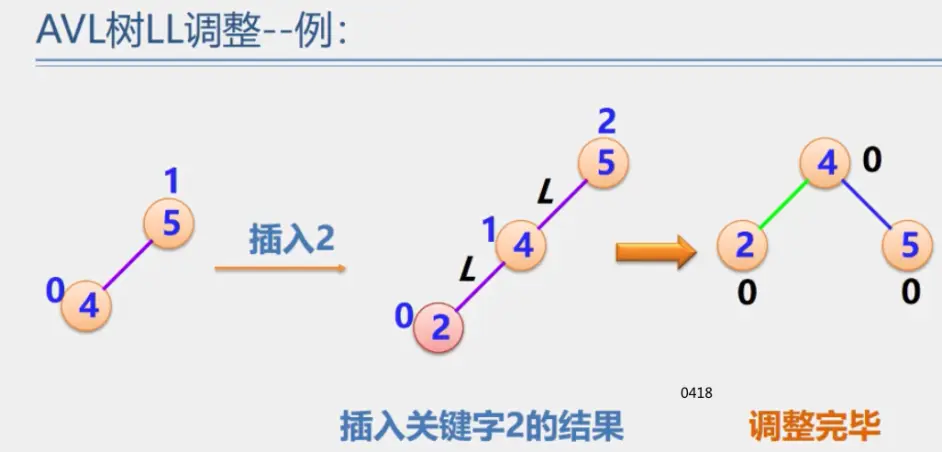
-
2<5 左子树 2<4 左子树
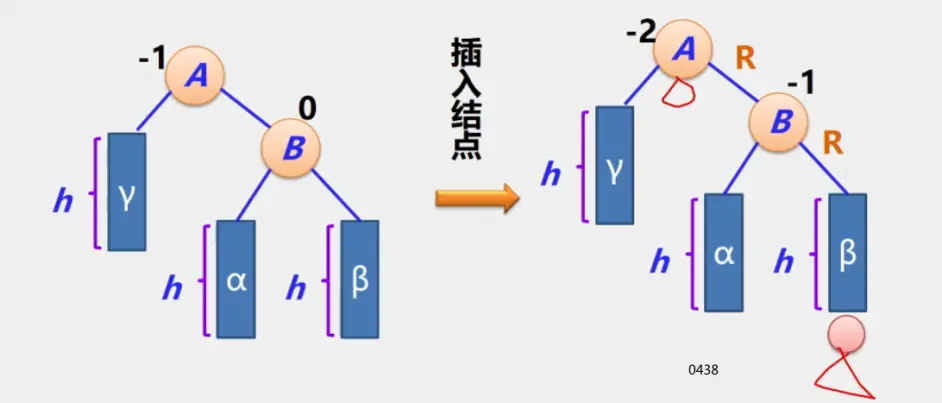
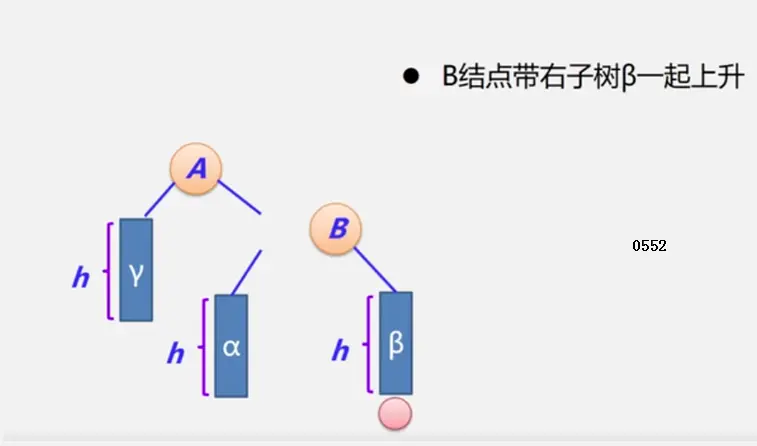
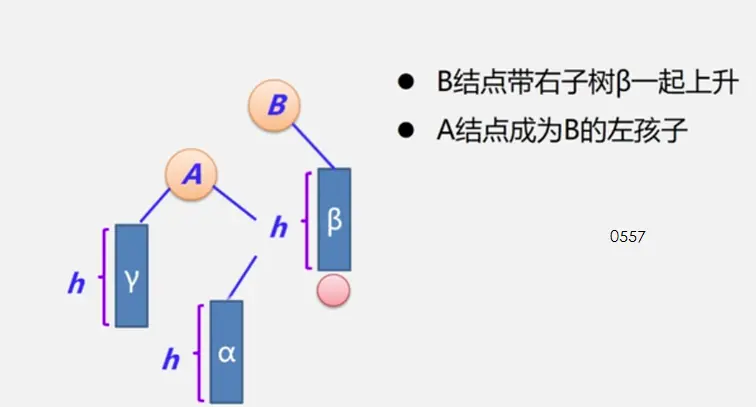
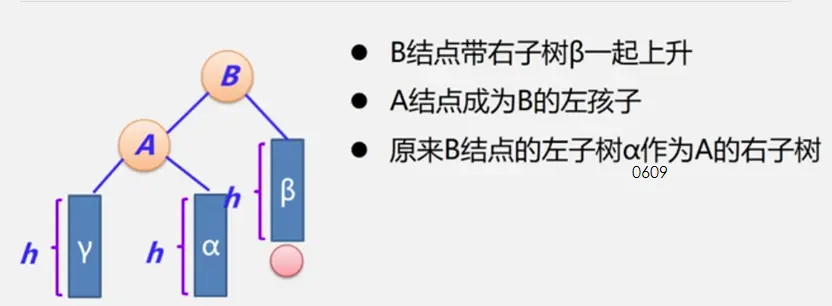
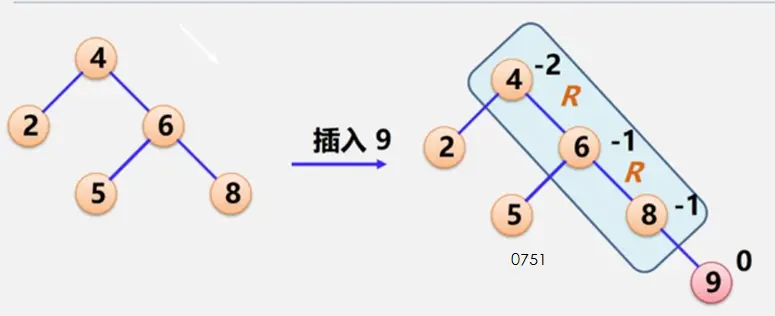
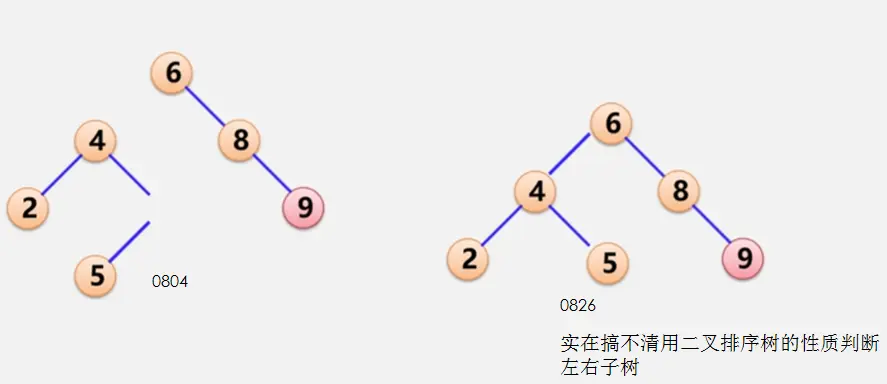
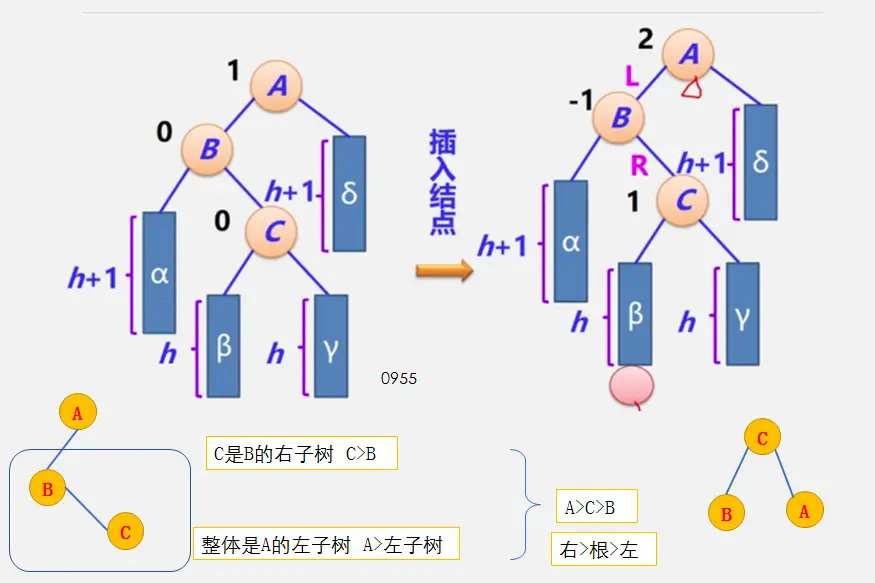
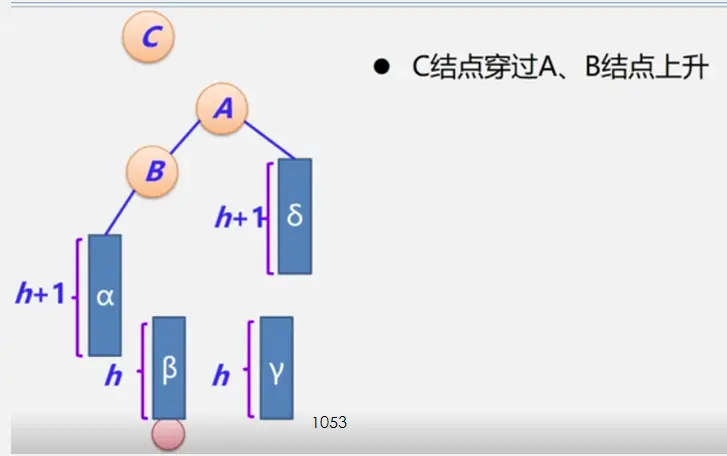
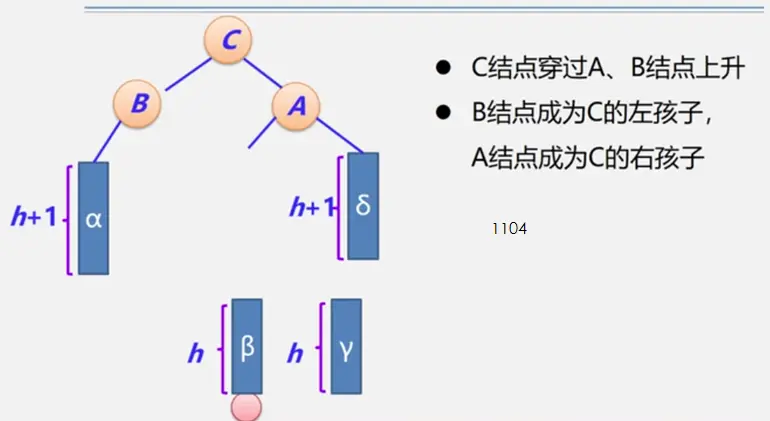
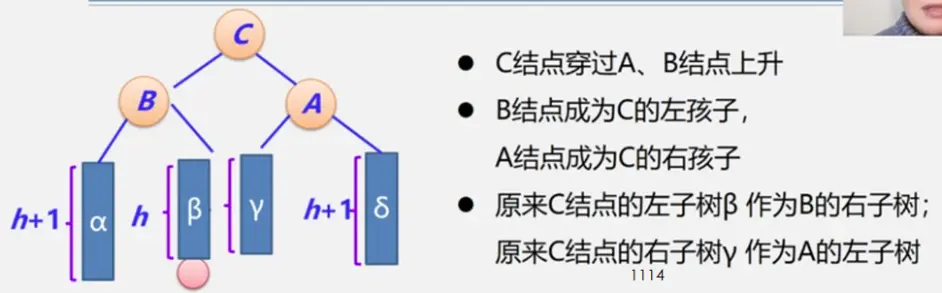
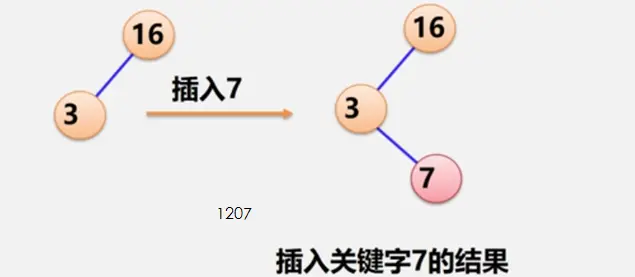
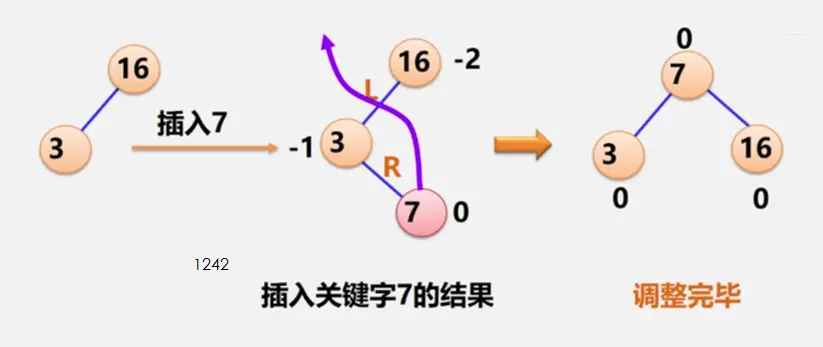
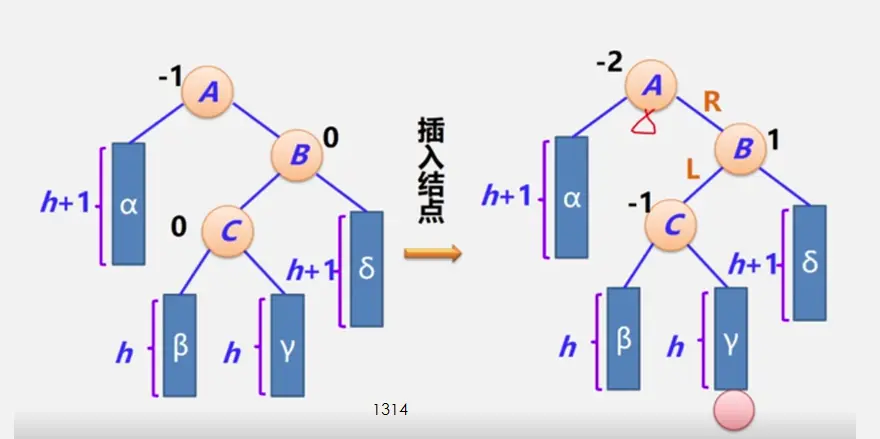
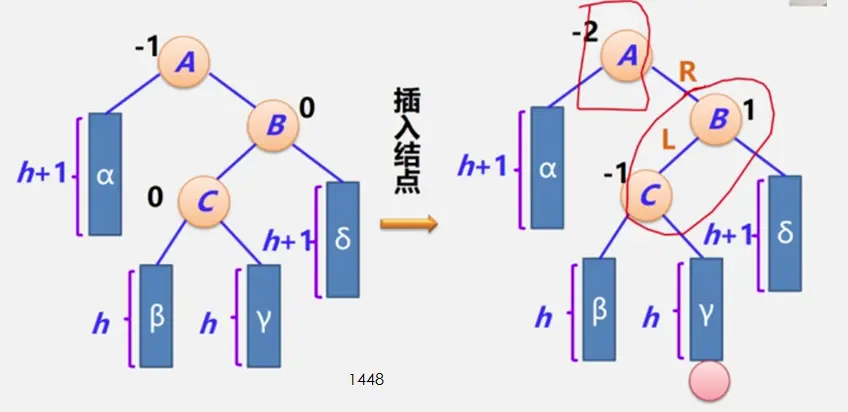
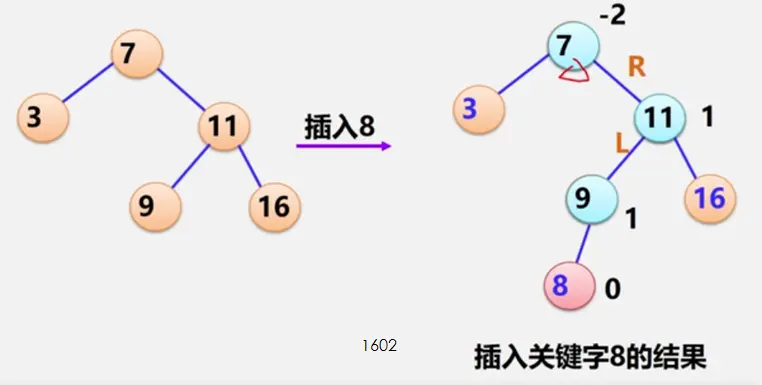
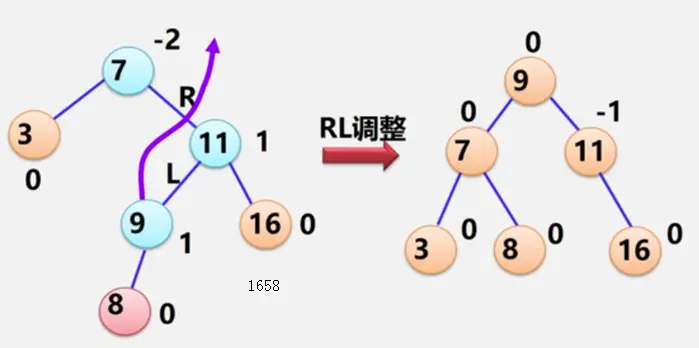
调整方法——例题
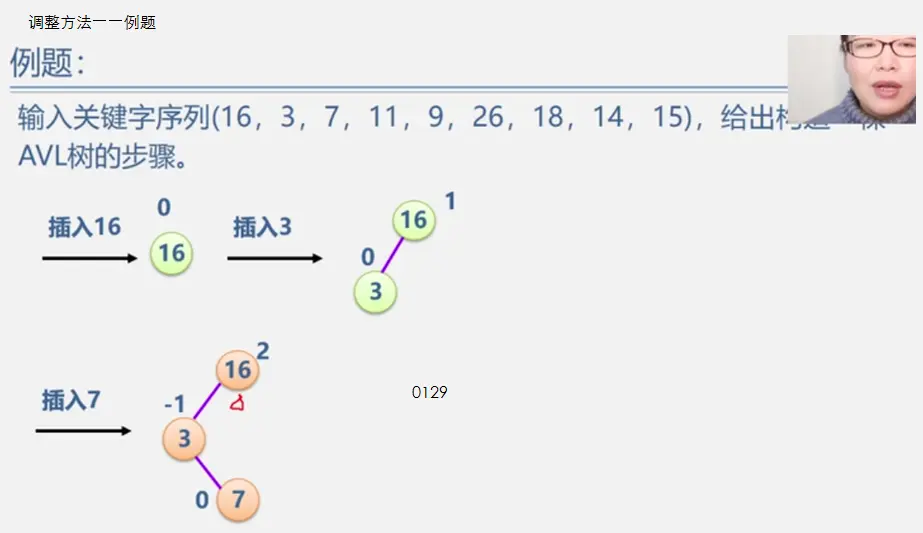
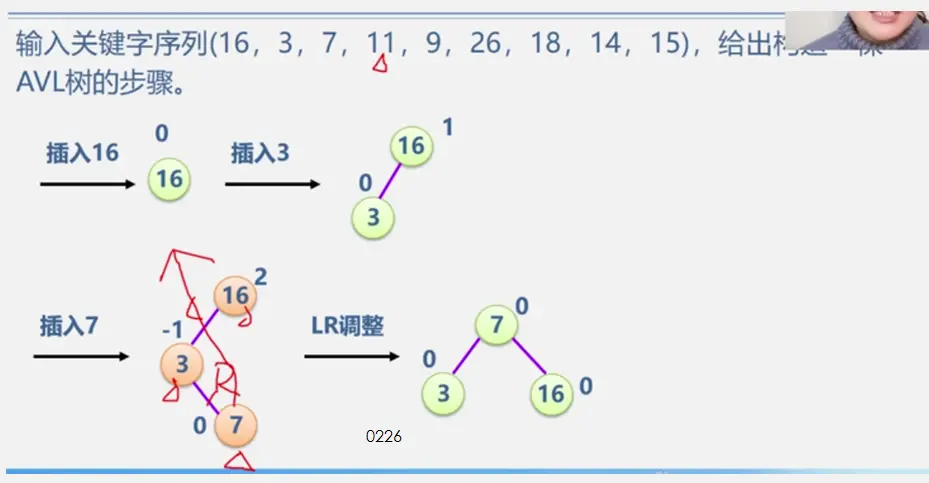
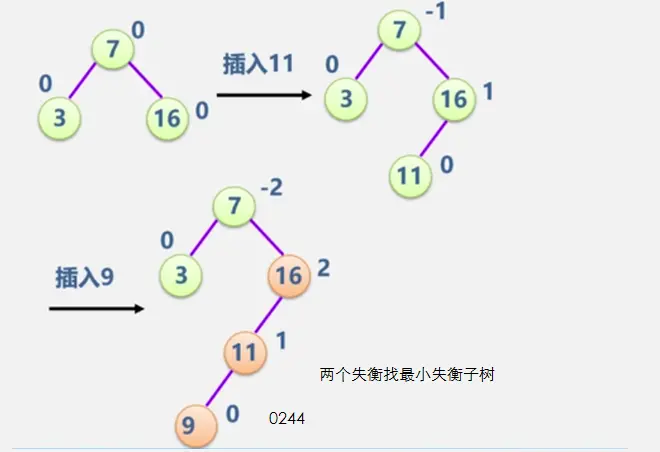
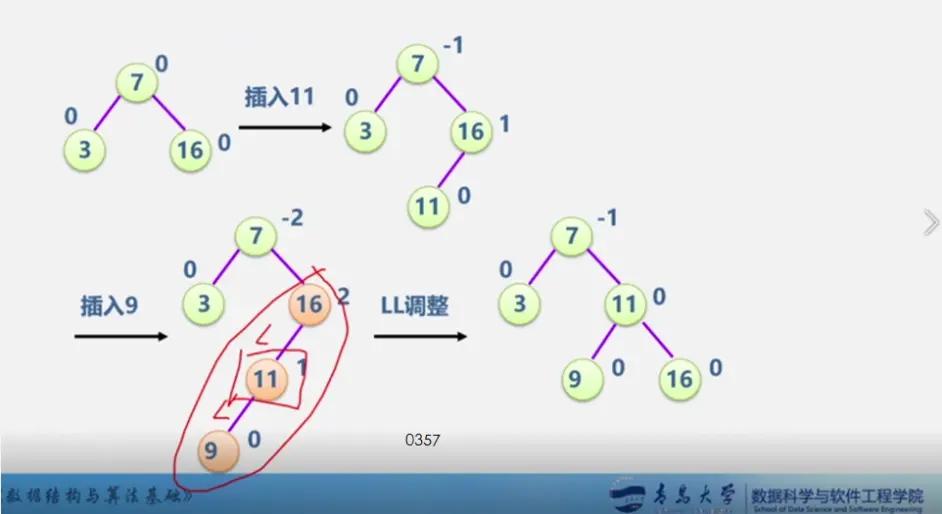
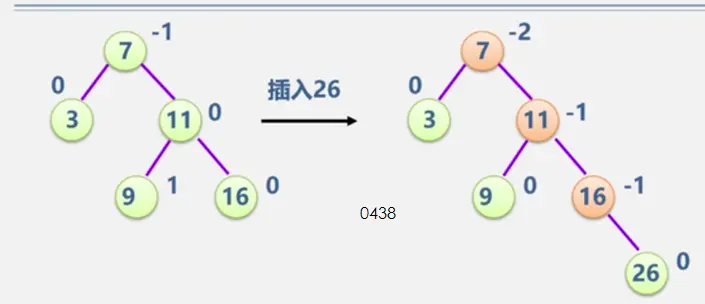
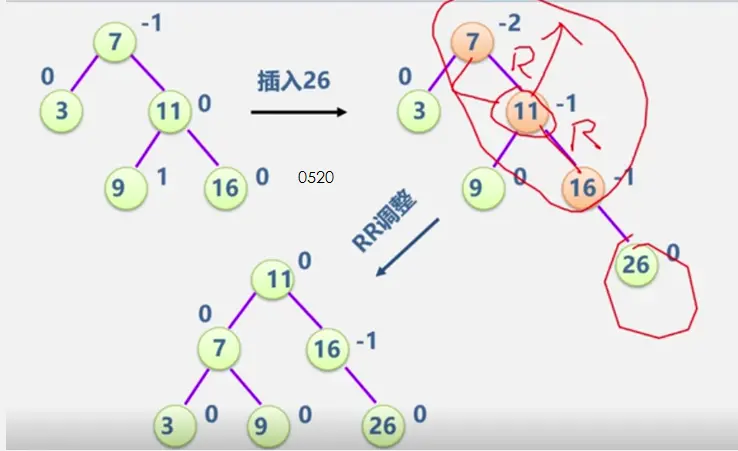
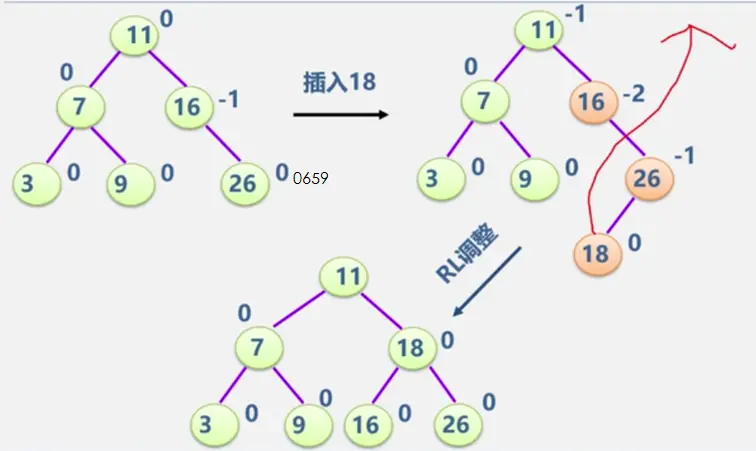
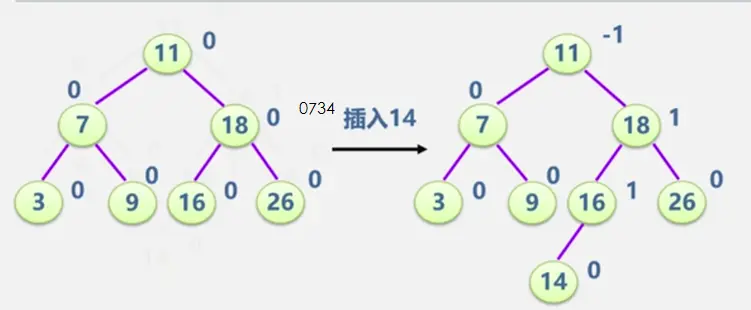
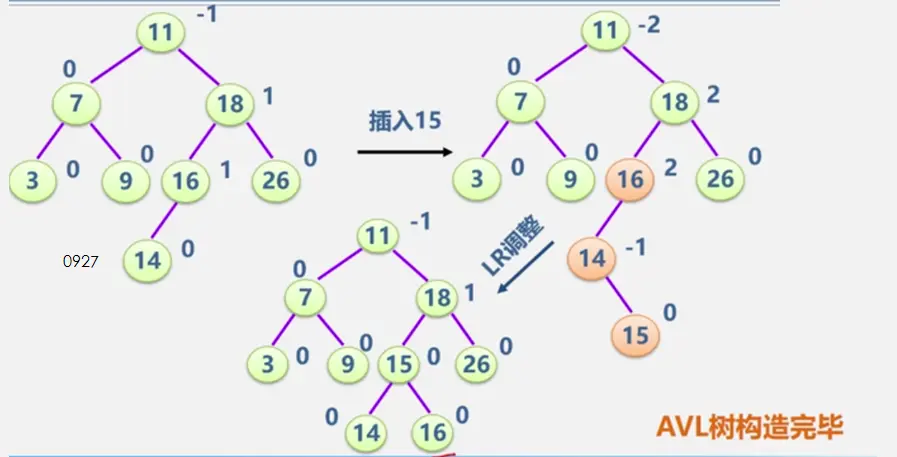
哈希表
散列表的基本概念
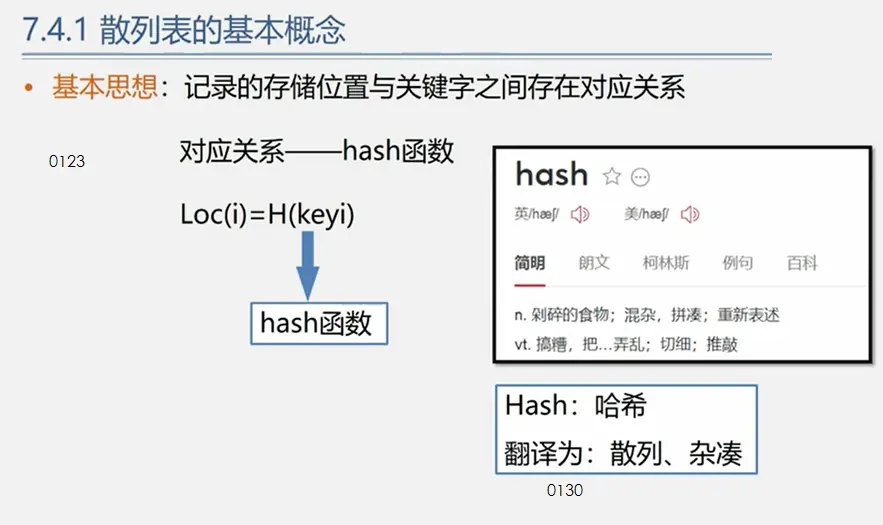
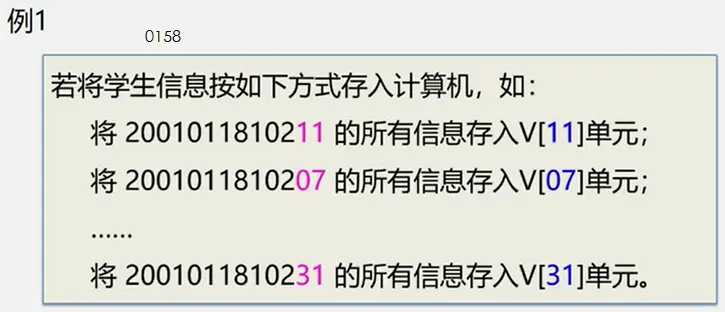

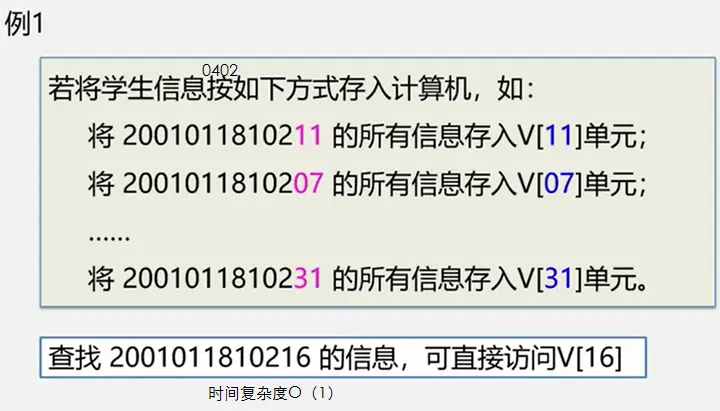
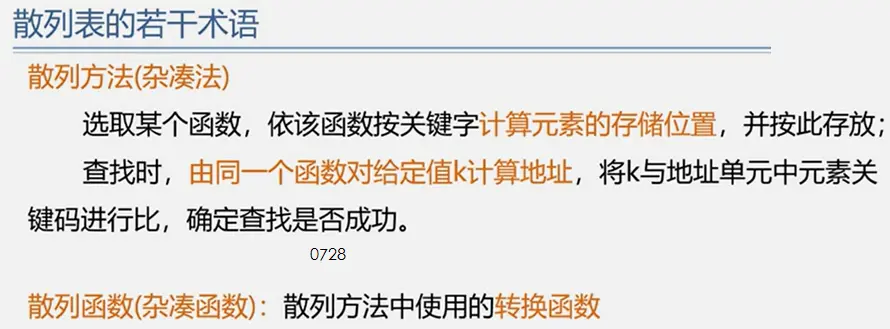
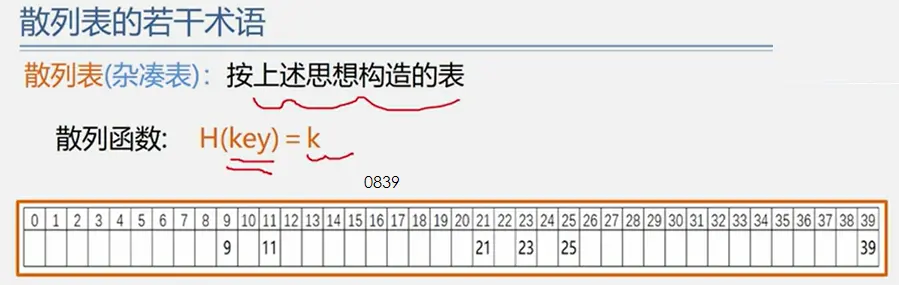
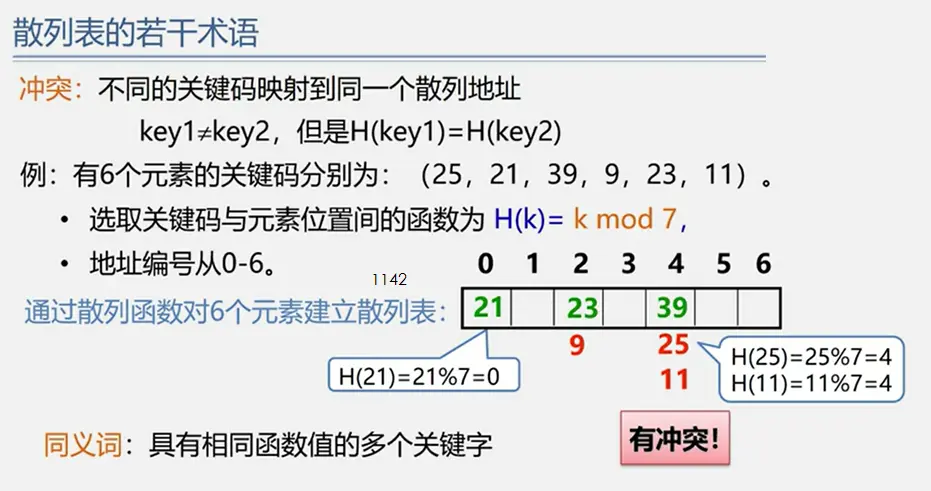
散列函数的构造



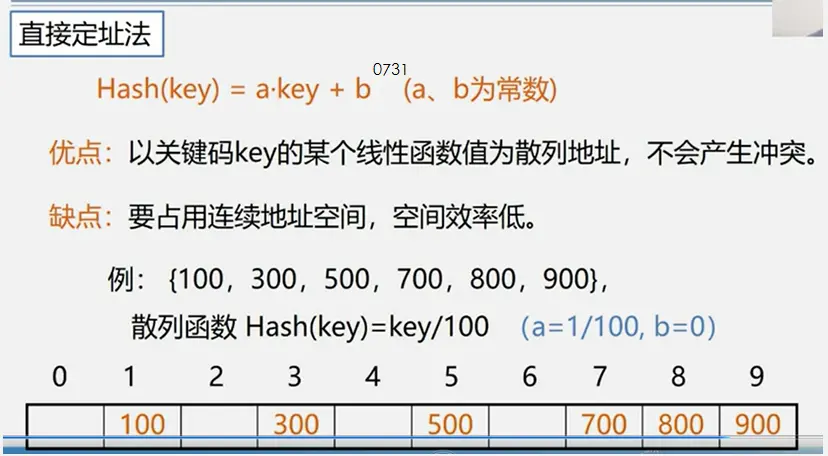

直接寻址法:直接定址法是以数据元素关键字k本身或它的线性函数作为它的哈希地址, 实际生活中,关键字的元素很少是连续的。用该方法产生的哈希表会造成空间大量的浪费,因此这种方法适应性并不强
数字分析法:数字分析法是取数据元素关键字中某些取值较均匀的数字位作为哈希地址的方法。即当关键字的位数很多时,可以通过对关键字的各位进行分析,丢掉分布不均匀的位,作为哈希值它只适合于所有关键字值已知的情况。通过分析分布情况把关键字取值区间转化为一个较小的关键字取值区间。
平方取中法:这是一种常用的哈希函数构造方法。这个方法是先取关键字的平方,然后根据可使用空间的大小,选取平方数是中间几位为哈希地址。
哈希函数 H(key)=key^2的中间几位”因为这种方法的原理是通过取平方扩大差别,平方值的中间几位和这个数的每一位都相关,则对不同的关键字得到的哈希函数值不易产生冲突,由此产生的哈希地址也较为均匀。
折叠法,所谓折叠法是将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位),这方法称为折叠法。
随机数法,
除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取,素数,质数,或m,若p选的不好,容易产生同义词 摘自:哈希表
那么对p 的选择,关键字不仅可以通过直接对取模,还可以在上述数字分析,平方取中,折叠之后,在进行取模。这样使得关键字在通过hash函数映射到内存单元的任意地址是均匀的,减少冲突。
在取模的过程中对P为什么要使用质数或素数呢?
因为质数是只有1和他本身的因子。而合数除了1和他本身外还有其他因子。这样在取模的时候,就会出现相同的hash地址,进而增加冲突。 b = ak +n n为取余之后的值,那么当a为合数的时候,同样是n,k的取值或b的取值是密集,增加冲突。
处理冲突的方法
开地址法


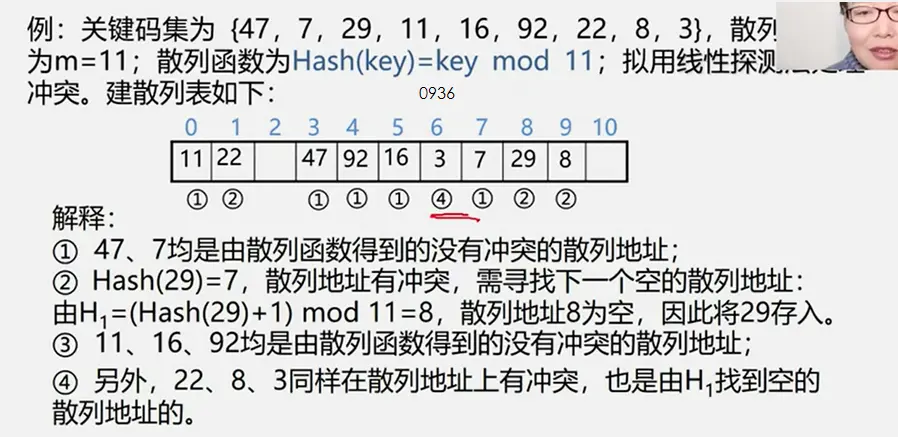
当前位置不行就增加1 加1不行就加2
查找11 11mod11 =0 先去0号位置 结果找到了
查找22 22mod11=0 先去0号位置 结果没找到 去1(0+1)号找 1号找不到去2(0+2)号找[线性探测的增量是 1 2 3 ...]
平均查找长度(1+2+1+1+1+4+1+2+2)/9(假设概率相同P=1/9)=1.67
地址对任何元素都开放(可用)

黑色字体 直接存



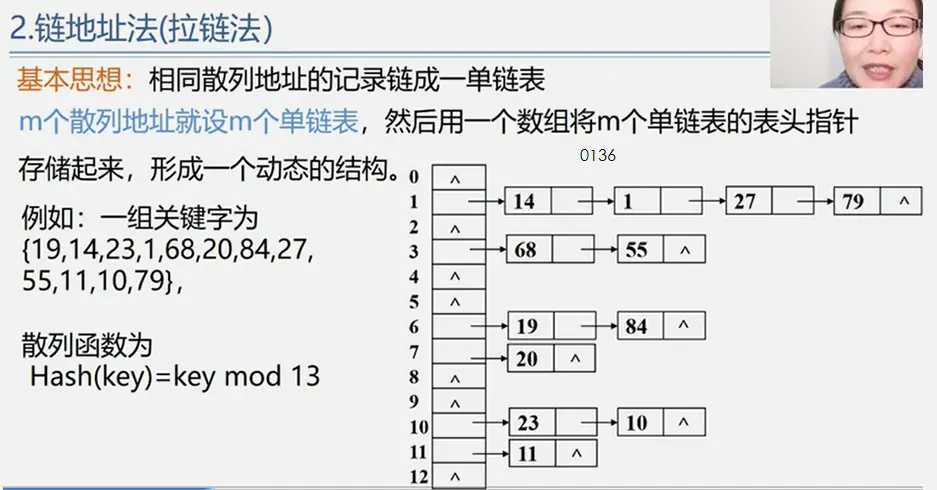

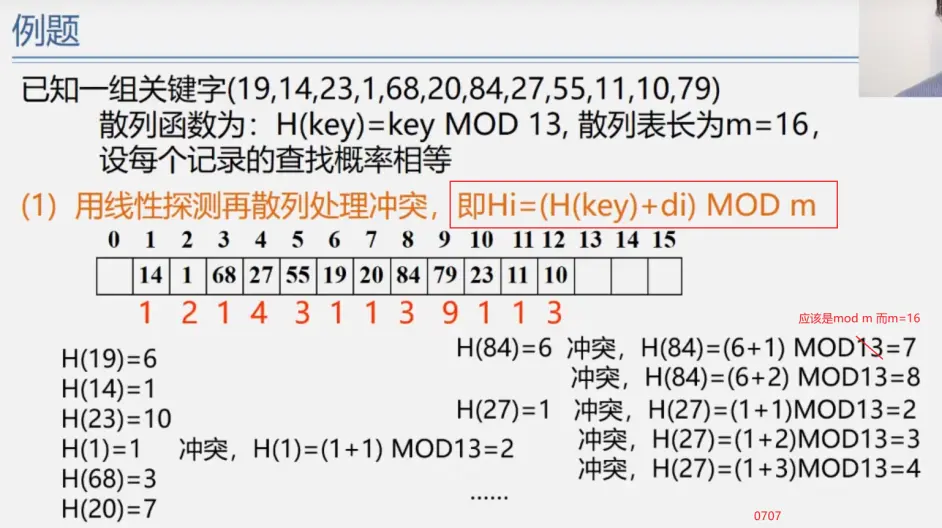
除留余数法
- 先构造散列表
- 查找方法 查找19 H(19)=19 mod 13 = 6
- 查找84 H(84)=84 mod 13 = 6 到6号位置上不是84 接着去7号也不是84 再去8号位置 是84 比较3次
- 红色字是找到这个元素需要比较的次数
- 平均查找长度:ASL=(16+2+33+4+9)/12=2.5

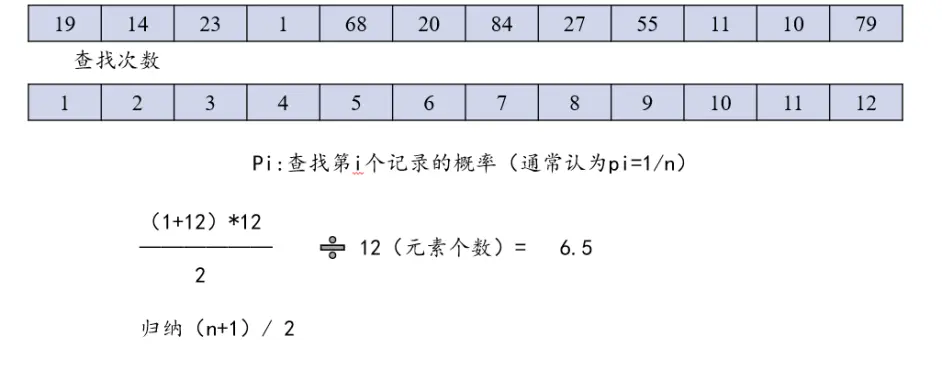
有序表折半查找的ASL log2(n+1) - 1 =二点多
散列表上查找的ASL 如果完全没有冲突可能达到 O(1)
散列表的效率分析:
ASL取决于
散列函数:能否让关键字均匀的排列在散列表中
处理冲突的方法:

散列表的填装因子α(alpha): n=12 哈希表的长度=16 α=12/16 = 0.75

哈希表C++实现(极其偷懒的一种实现,大致思想如示,深入可以参考STL中HashTable的实现)
#include <iostream>
using namespace std;
class HashItem {
private:
string val; // 数据
int key; // 碰撞次数
public:
HashItem(string val, int key)
: key(key), val(val) {}
const string &getVal() const { return val; }
const int &getKey() const { return key; }
};
class HashTable {
int SIZE;
HashItem **table;
public:
explicit HashTable(int size) {
this->SIZE = size;
table = new HashItem *[SIZE]();
}
void set(int key, string val) {
int idx = key % SIZE;
while (table[idx] && table[idx]->getKey() != key)
idx = (idx + 1) % SIZE;
table[idx] = new HashItem(val, key);
}
string get(int key) {
int idx = key % SIZE;
while (table[idx] && table[idx]->getKey() != key)
idx = (idx + 1) % SIZE;
return table[idx] ? table[idx]->getVal() : "nullptr";
}
~HashTable() {
for (int i = 0; i < SIZE; i++)
if (table[i]) delete table[i];
delete[] table;
}
};
int main() {
HashTable ht(11);
ht.set(47, "创新_智科");
ht.set(7, "21");
ht.set(29, "数据结构");
ht.set(11, "散列表");
ht.set(16, "线性探测再散列");
ht.set(92, "除留余数法");
ht.set(22, "纯混子");
ht.set(8, "的");
ht.set(3, "实现");
cout << ht.get(7) << ht.get(47) << ht.get(22)
<< ht.get(8) << ht.get(29) << ht.get(11)
<< ht.get(92) << ht.get(16) << ht.get(3);
return 0;
}
排序
直接插入排序
1、算法思想:直接插入排序是指,将一个新记录插入到已经排序好的有序表当中,然后得到一个新的有序表。
即:先将有序表序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
2、算法要点:要注意设立哨兵,让哨兵充当临时存储和判断数组边界的使者。
3、算法稳定性:直接插入算法是稳定的。
4、算法top:如果执行一个和插入元素相等的数据进行插入排序,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序。
5、直接插入算法的时间复杂度:
public class StraightInsertion {
static void straightInsertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int e = array[i];
int j;
for (j = i - 1; j > 0 && e < array[j]; j--) {
array[j + 1] = array[j];
}
array[j + 1] = e;
}
}
}
shell排序
定义一个呈递减变化的步长gap,假设数组长度为size,最开始定义的步长为gap=size/2,并从第0个元素开始,将数组中间隔为gap的元素构成子数组,共构成gap个子数组,之后对每个子数组进行排序(排序方法任意),此时第一步就算完成了;然后定义第二步的步长为gap=gap/2,并做与第一步相同的操作;以此类推,每次取步长为gap=gap/2,直到对gap为1的数组进行排序后,整个排序过程结束。
为了更好地理解该排序算法的思想,我们来看下面的图片:
从上图可以知道,原始数组为:10 8 6 20 4 3 22 1 0 15 16,以排升序为例,接下来进行分步操作。
第一步:由于数组长度size=11,故gap=11/2=5,故共分为5个子数组,分别对这5个子数组进行排序后,数组变化为:3 8 1 0 4 10 22 6 20 15 16。
第二步:由于第一步的gap为5,故该步骤的gap=5/2=2,但可以看到图片上的gap为3,这是由于图片作者失误导致的,在后面的算法实现中,本文作者不会出现类似的错误,读者大可放心。但这不影响我们来掌握希尔排序的思想,我们根据图片中的gap为3,故共分成3个子数组,分别对这3个子数组进行排序后,数组变化为:0 4 1 3 6 10 15 8 20 22 16。
第三步:由于第二步的gap为3,故该步骤的gap=3/2=1,故共分为1个子数组,对这1个子数组进行排序后,数组变化为:0 1 3 4 6 8 10 15 16 20 22。
public class ShellSort {
private static void shellInSort(int[] array, int incr){
for(int i = incr; i < array.length; i++){
int e = array[i];
int j;
for(j = i - incr ; j >= 0 && e < array[j]; j -= incr){
array[j +incr] = array[j];
}
array[j + incr] = e;
}
}
public static void shellSort(int[] array, int inc[]){
for (int j : inc) {
shellInSort(array, j);
}
}
}
冒泡排序
基本思想是对所有相邻记录的关键字值进行比效,如果是逆顺(a[j]>a[j+1]),则将其交换,最终达到有序化;
其处理过程为:
(1)将整个待排序的记录序列划分成有序区和无序区,初始状态有序区为空,无序区包括所有待排序的记录。
(2)对无序区从前向后依次将相邻记录的关键字进行比较,若逆序将其交换,从而使得关键字值小的记录向上”飘浮”(左移),关键字值大的记录好像石块,向下“堕落”(右移)。 每经过一趟冒泡排序,都使无序区中关键字值最大的记录进入有序区,对于由n个记录组成的记录序列,最多经过n-1趟冒泡排序,就可以将这n个记录重新按关键字顺序排列。
public class BubbleSort {
public static void bubbleSort(int[] array){
for(int i = 1; i < array.length; i++){
for(int j = 0; j < array.length - i; j++){
if(array[j] > array[j + i]){
array[j] = array[j] ^ array[j + 1];
array[j + 1] = array[j] ^ array[j + 1];
array[j] = array[j] ^ array[j + 1];
}
}
}
}
}
快速排序
1、快速排序的基本思想:
快速排序使用分治的思想,通过一趟排序将待排序列分割成两部分,其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
2、快速排序的三个步骤:
(1)选择基准:在待排序列中,按照某种方式挑出一个元素,作为 "基准"(pivot)
(2)分割操作:以该基准在序列中的实际位置,把序列分成两个子序列。此时,在基准左边的元素都比该基准小,在基准右边的元素都比基准大
(3)递归地对两个序列进行快速排序,直到序列为空或者只有一个元素。
3、选择基准的方式
对于分治算法,当每次划分时,算法若都能分成两个等长的子序列时,那么分治算法效率会达到最大。也就是说,基准的选择是很重要的。选择基准的方式决定了两个分割后两个子序列的长度,进而对整个算法的效率产生决定性影响。
最理想的方法是,选择的基准恰好能把待排序序列分成两个等长的子序列
public class QuickSort {
public static void quickSort(int[] array, int begin, int end){
if(begin > end) return;
int temp = array[begin];
int i = begin;
int j = end;
while(i != j){
while(array[j] >= temp && j > i) j--;
while(array[i] <= temp && j > i) i++;
if(j > i){
array[i] = array[i]^array[j];
array[j] = array[i]^array[j];
array[i] = array[i]^array[j];
}
}
array[begin] = array[i];
array[i] = temp;
quickSort(array, begin, i - 1);
quickSort(array, i + 1, end);
}
}
归并排序
归并排序算法实现
-
归并排序的核心思想其实很简单,如果要排序一个数组,我们先把数组从中间分成前后两部分,然后分别对前后两部分进行排序,再将排好序的两部分数据合并在一起就可以了。
-
归并排序使用的是分治思想,分治也即是分而治之,将一个大问题分解为小的子问题来解决。分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧。
-
如果要对数组区间 [p, r] 的数据进行排序,我们先将数据拆分为两部分 [p, q] 和 [q+1, r],其中 q 为中间位置。对两部分数据排好序后,我们再将两个子数组合并在一起。当数组的起始位置小于等于终止位置时,说明此时只有一个元素,递归也就结束了。
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解
- 对两个子数组进行合并的过程如下所示,我们先建立一个临时数组,然后从两个子数组的起始位置开始比较,将较小的元素一个一个放入临时数组,直到其中一个子数组比较完毕,再将剩下的另一个子数组余下的值全部放到临时数组后面。最后我们需要将临时数组中的数据拷贝到原数组对应的位置。

算法分析
-
归并排序是一个稳定的排序算法,在进行子数组合并的时候,我们可以设置当元素大小相等时,先将前半部分的数据放入临时数组,这样就可以保证相等元素在排序后依然保持原来的顺序。
-
从我们的分析可以看出,归并排序的执行效率与原始数据的有序程度无关,其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
-
归并排序有一个缺点,那就是它不是原地排序算法。在进行子数组合并的时候,我们需要临时申请一个数组来暂时存放排好序的数据。因为这个临时空间是可以重复利用的,因此归并排序的空间复杂度为 O(n),最多需要存放 n 个数据。
代码实现
package com.drizzledrop.Sort;
public class MergeSort {
public static void mergeSort(int[] array){
int []temArray = new int[array.length];
mergeSortHelp(array, temArray, 0, array.length - 1);
}
private static void mergeSortHelp(int[] array, int[] tempArray, int low, int high){
if(low < high){
int mid = low + ((high - low) >> 1);
mergeSortHelp(array,tempArray, low, mid);
mergeSortHelp(array,tempArray, mid + 1, high);
merge(array, tempArray, low, mid, high);
}
}
private static void merge(int[] array, int[] tempArray, int low, int mid, int high){
int i, j, k;
for(i = low, j = mid + 1, k = low; i <= mid && j <= high; k++){
if(array[i] <= array[j]){ // array[i]较小,先归并
tempArray[k] = array[i];
i++;
}
else{
tempArray[k] = array[j]; // array[j]较小,先归并
j++;
}
}
for(; i <= mid; i++, k++){ // 归并array[low..mid]中剩余元素
tempArray[k] = array[i];
}
for(; j <= high; j++, k++){// 归并array[mid+1..high]中剩余元素
tempArray[k] = array[j];
}
for(i = low; i <= high; i++){// 将tempArray[low..high]复制到array[low..high]
array[i] = tempArray[i];
}
}
}
堆排序
大小根堆
性质:每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆。如下图
我们对上面的图中每个数都进行了标记,上面的结构映射成数组就变成了下面这个样子
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
1.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2**i*+1
3.右孩子索引:2**i*+2
所以上面两个数组可以脑补成堆结构,因为他们满足堆的定义性质:
大根堆:arr(i)>arr(2i+1) && arr(i)>arr(2i+2)
小根堆:arr(i)<arr(2i+1) && arr(i)<arr(2i+2)
堆排序基本步骤
基本思想:
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
2.1 构造堆
将无序数组构造成一个大根堆(升序用大根堆,降序就用小根堆)
假设存在以下数组
主要思路:第一次保证00位置大根堆结构(废话),第二次保证01位置大根堆结构,第三次保证02位置大根堆结构...直到保证0n-1位置大根堆结构(每次新插入的数据都与其父结点进行比较,如果插入的数比父结点大,则与父结点交换,否则一直向上交换,直到小于等于父结点,或者来到了顶端)
插入6的时候,6大于他的父结点3,即arr(1)>arr(0),则交换;此时,保证了0~1位置是大根堆结构,如下图:
-
(注:待交换的数为蓝色,交换后的数为绿色)
插入8的时候,8大于其父结点6,即arr(2)>arr(0),则交换;此时,保证了0~2位置是大根堆结构,如下图
插入5的时候,5大于其父结点3,则交换,交换之后,5又发现比8小,所以不交换;此时,保证了0~3位置大根堆结构,如下图
插入7的时候,7大于其父结点5,则交换,交换之后,7又发现比8小,所以不交换;此时整个数组已经是大根堆结构
2.2 固定最大值再构造堆
此时,我们已经得到一个大根堆,下面将顶端的数与最后一位数交换,然后将剩余的数再构造成一个大根堆
- (注:黑色的为固定好的数字,不再参与排序)
此时最大数8已经来到末尾,则固定不动,后面只需要对顶端的数据进行操作即可,拿顶端的数与其左右孩子较大的数进行比较,如果顶端的数大于其左右孩子较大的数,则停止,如果顶端的数小于其左右孩子较大的数,则交换,然后继续与下面的孩子进行比较
下图中,5的左右孩子中,左孩子7比右孩子6大,则5与7进行比较,发现5<7,则交换;交换后,发现5已经大于他的左孩子,说明剩余的数已经构成大根堆,后面就是重复固定最大值,然后构造大根堆
如下图:顶端数7与末尾数3进行交换,固定好7,
剩余的数开始构造大根堆 ,然后顶端数与末尾数交换,固定最大值再构造大根堆,重复执行上面的操作,最终会得到有序数组
关于筛选,完整过程见:【排序算法】之堆排序
代码如下:
//堆排序
public static void heapSort(int[] arr) {
//构造大根堆
heapInsert(arr);
int size = arr.length;
while (size > 1) {
//固定最大值
swap(arr, 0, size - 1);
size--;
//构造大根堆
heapify(arr, 0, size);
}
}
//构造大根堆(通过新插入的数上升)
public static void heapInsert(int[] arr) {
for (int i = 0; i < arr.length; i++) {
//当前插入的索引
int currentIndex = i;
//父结点索引
int fatherIndex = (currentIndex - 1) / 2;
//如果当前插入的值大于其父结点的值,则交换值,并且将索引指向父结点
//然后继续和上面的父结点值比较,直到不大于父结点,则退出循环
while (arr[currentIndex] > arr[fatherIndex]) {
//交换当前结点与父结点的值
swap(arr, currentIndex, fatherIndex);
//将当前索引指向父索引
currentIndex = fatherIndex;
//重新计算当前索引的父索引
fatherIndex = (currentIndex - 1) / 2;
}
}
}
//将剩余的数构造成大根堆(通过顶端的数下降)
public static void heapify(int[] arr, int index, int size) {
int left = 2 * index + 1;
int right = 2 * index + 2;
while (left < size) {
int largestIndex;
//判断孩子中较大的值的索引(要确保右孩子在size范围之内)
if (arr[left] < arr[right] && right < size) {
largestIndex = right;
} else {
largestIndex = left;
}
//比较父结点的值与孩子中较大的值,并确定最大值的索引
if (arr[index] > arr[largestIndex]) {
largestIndex = index;
}
//如果父结点索引是最大值的索引,那已经是大根堆了,则退出循环
if (index == largestIndex) {
break;
}
//父结点不是最大值,与孩子中较大的值交换
swap(arr, largestIndex, index);
//将索引指向孩子中较大的值的索引
index = largestIndex;
//重新计算交换之后的孩子的索引
left = 2 * index + 1;
right = 2 * index + 2;
}
}
//交换数组中两个元素的值
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}

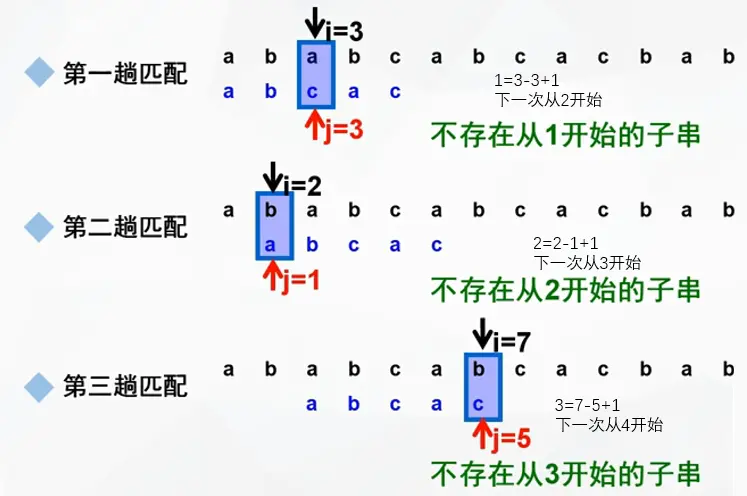
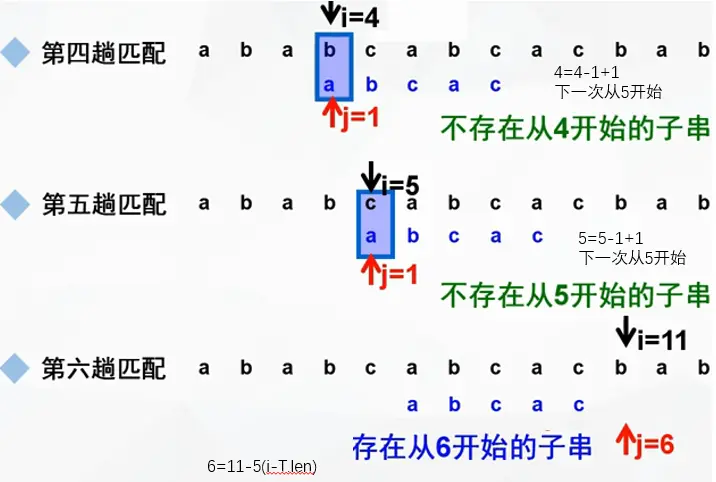
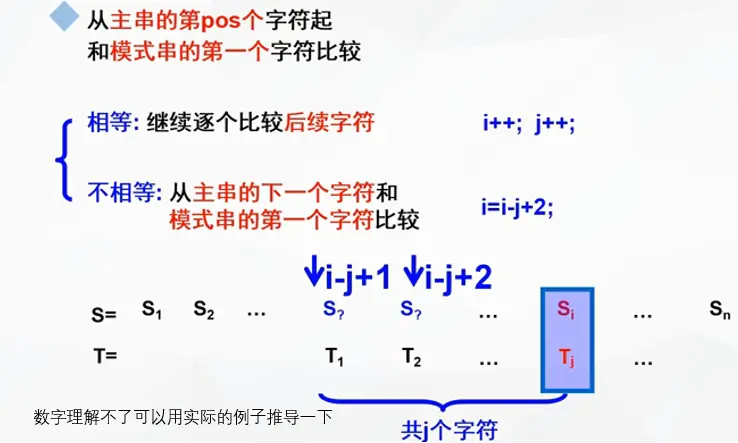
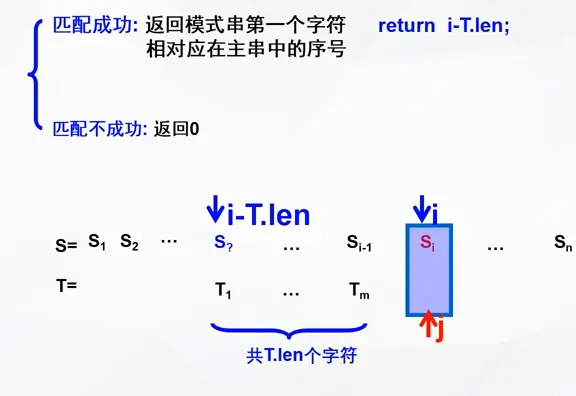



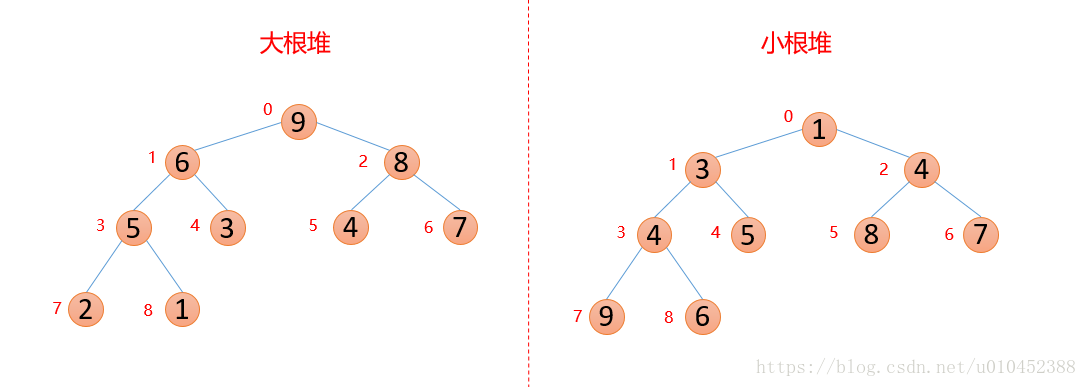

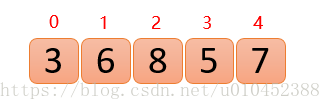
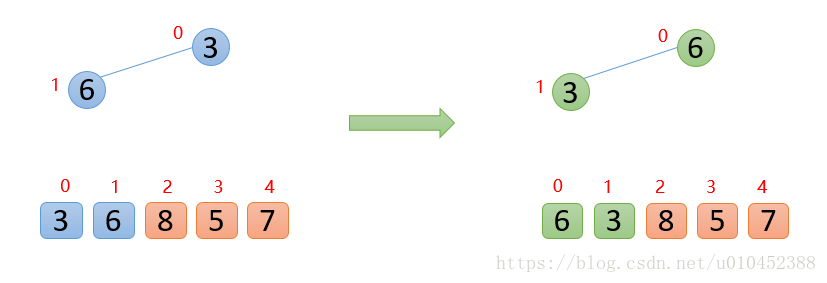
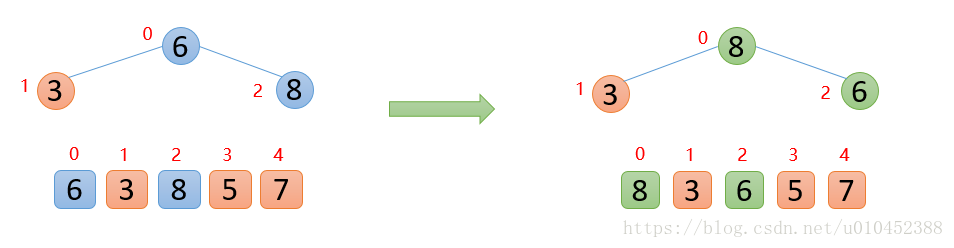
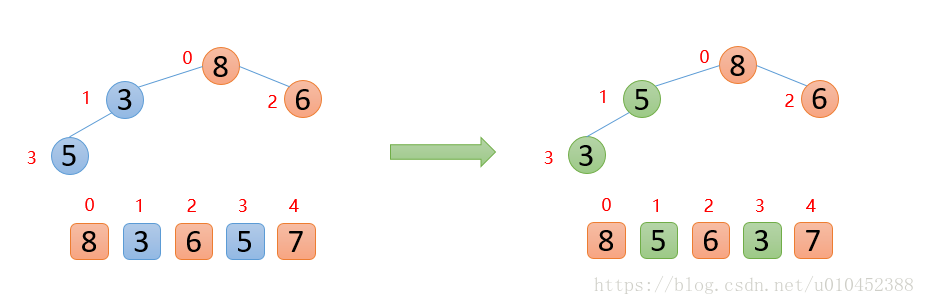
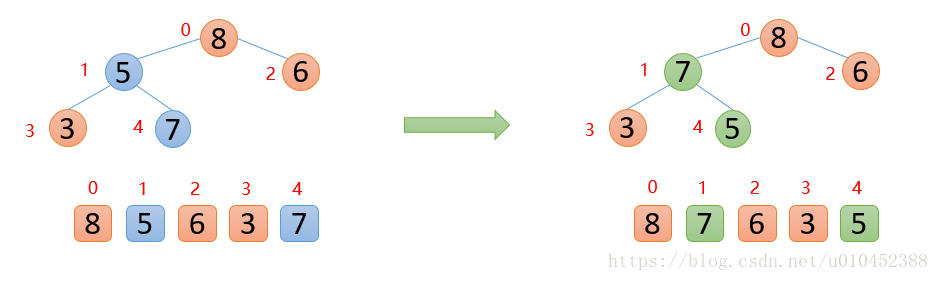
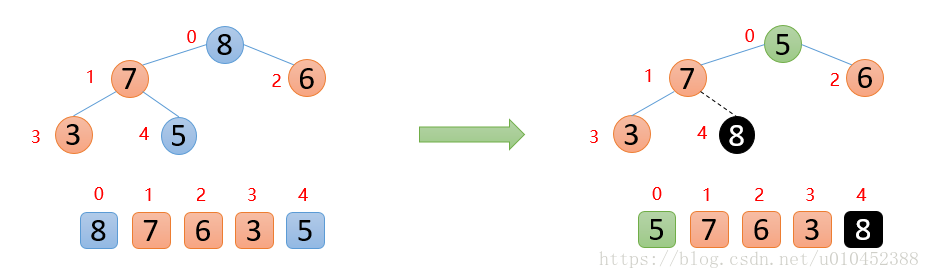
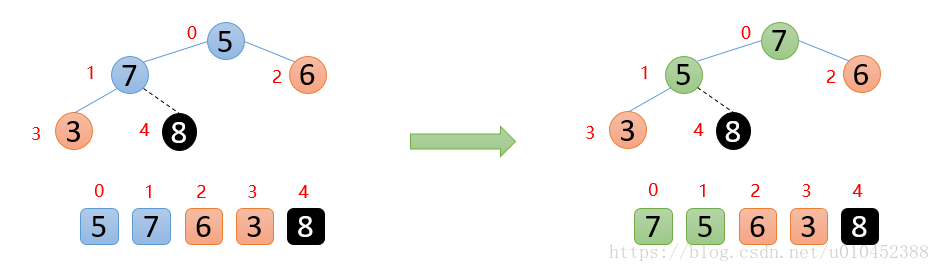
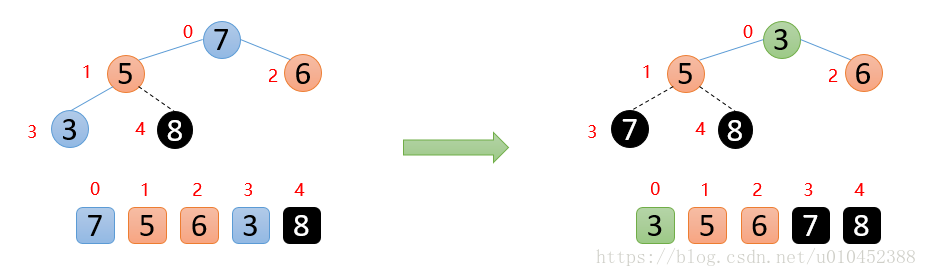
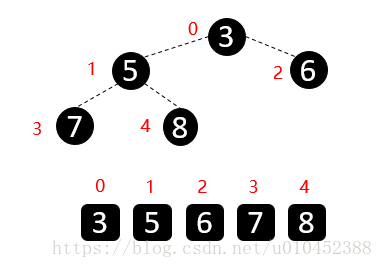


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY