吃土豆
时间限制:1000 ms | 内存限制:65535 KB
难度:4
- 描述
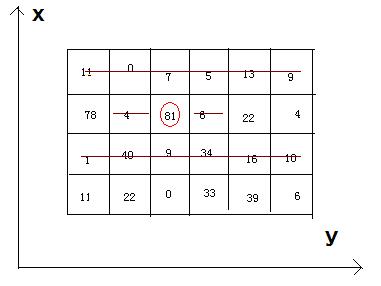
- Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.
Now, how much qualities can you eat and then get ?- 输入
- There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M,N<=500.
- 输出
- For each case, you just output the MAX qualities you can eat and then get.
- 样例输入
-
4 6 11 0 7 5 13 9 78 4 81 6 22 4 1 40 9 34 16 10 11 22 0 33 39 6
- 样例输出
-
242
- 来源
- 2009 Multi-University Training Contest 4
- 题解:
- 仔细想想,其实这道题横坐标和纵坐标的状态是一样的,
对于取点(i, j):
则在列上,不能取旁边相邻的两列,即 j-1 列和 j+1 列;
同理,在行上,不能取旁边相邻的两行,即 i-1 行和 i+1 行。
所以,可以对行和列单独考虑:
对于列级状态转移方程: map[i][j] = max (map[i][j-2],map[i][j-3]);
对于行级状态转移方程: dp[i] = max(dp[i-2], dp[i-3]) + max( map[i][n-1], map[i][n]);(假定一共有n列) - 参考 :http://www.cnblogs.com/A-way/archive/2013/05/08/3066236.html
-
1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 5 using namespace std; 6 7 int main() 8 { 9 int n, m; 10 int map[505][505], dp[505]; 11 12 while(~scanf("%d%d", &n, &m)) 13 { 14 memset(map, 0, sizeof(map)); 15 memset(dp, 0, sizeof(dp)); 16 17 for(int i = 3; i < n+3; ++i) 18 for(int j = 3; j < m+3; ++j) 19 { 20 scanf("%d", &map[i][j]); 21 map[i][j] += max(map[i][j-2], map[i][j-3]); 22 } 23 24 for(int i = 3; i < n+3; ++i) 25 dp[i] = max(dp[i-2], dp[i-3]) + max(map[i][m+1], map[i][m+2]); 26 printf("%d\n", dp[n+2]); 27 } 28 return 0; 29 }
功不成,身已退