博客作业04--树
1.学习总结(2分)
1.1树结构思维导图
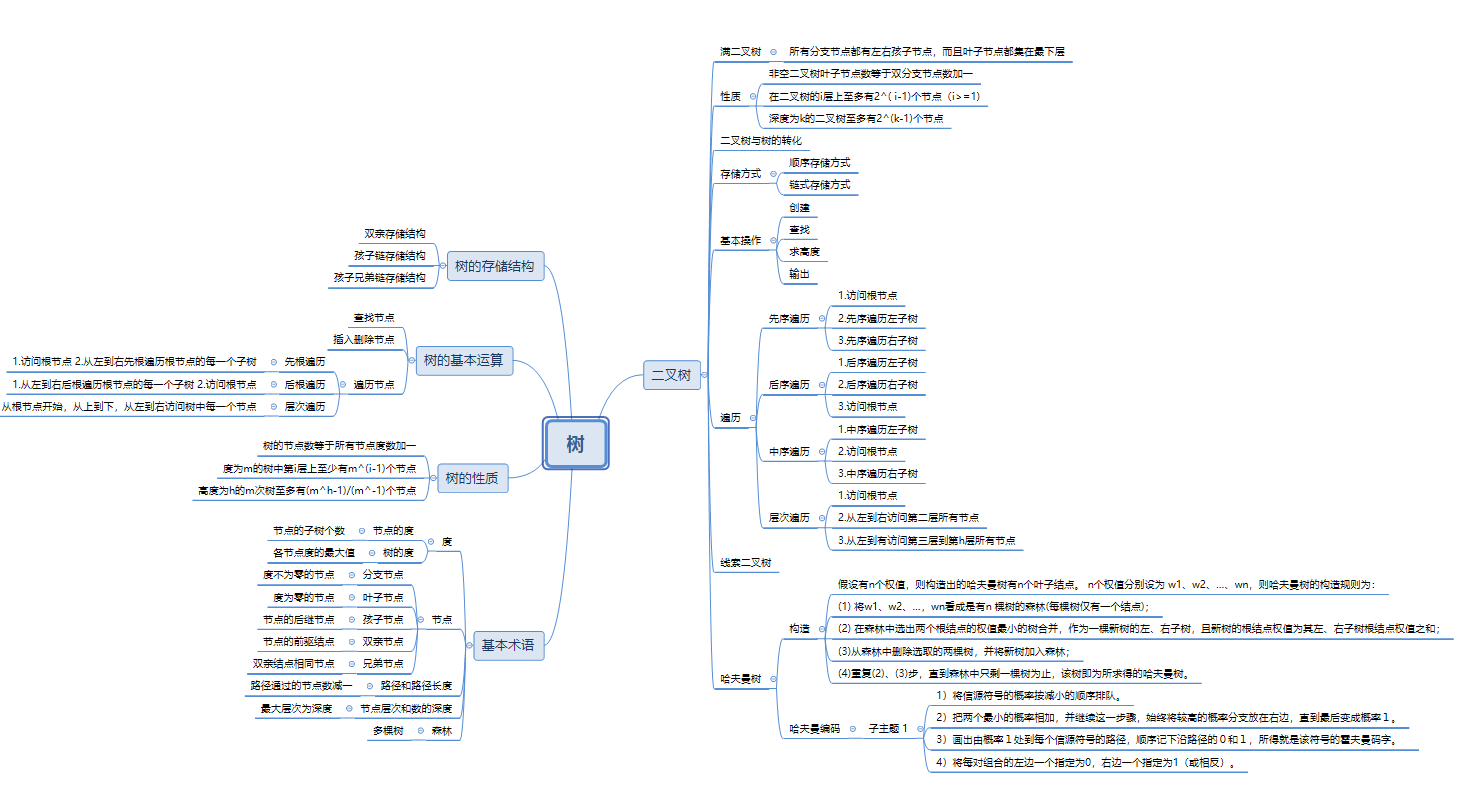
1.2 树结构学习体会
谈谈你对树结构认识,学习这个结构是否遇到哪些困难及树结构可以解决的问题。
树结构是很实用的一种抽象数据结构,在计算机中应用很广,计算机中的文件存储结构就是一种树的方式,虽然构建起来没有有线性表那样方便,有些构建方式甚至要用到队列或栈来辅助构建,但是有些有点是线性表不具备的,比如查找二叉树的效率比线性查找高的多,很多方面树的应用将使问题解决的效率得到很大提升,比如哈夫曼树就为通讯内容的压缩起到很大帮助。
困难:树的构建就有很多种方法,以及各种遍历方式,还有递归和非递归的方式,方法太多,所以做的时候很容易混乱,一下子写不出来。
解决的问题:二叉搜索树,哈夫曼编码,并查集,家谱处理等。
2.PTA实验作业(4分)
题目1:6-4 jmu-ds-表达式树
设计思路(伪代码或流程图)
void InitExpTree(BTree &T,string str) {
初始化一个节点栈和一个运算符栈
遍历字符串
if(字符是数字)
创建一个节点存该字符
并把该节点入栈
else
if(运算符栈空)
将第一个运算符入栈
else
比较要入栈的字符与栈顶字符
if(比栈顶字符优先级高)
入栈
else
将栈顶字符出栈到优先级比要入栈字符低或站栈空再入栈,
出栈时也要让节点栈出栈两个元素,根据出栈运算符进行
运算,结果生成新的节点,将该节点再入栈
遍历结束后如果运算符栈不空,进行如上出栈操作
最后树的根节点为节点栈的栈顶元素
}//建表达式的二叉树
double EvaluateExTree(BTree T){
建立运算数栈
定义变量num统计运算结果,n1,n2存从栈中取出的数
后序遍历树
if(节点的值是运算数)
入栈
else if(节点是操作符)
出栈两个运算数,根据操作符运算
结果存到num,num入栈
遍历结束后返回num
}//计算表达式树
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)




PTA提交列表说明。
一开始只是简单的按照想法写了出来,提交上去,全部都错误,于是从后面的点往前该,将除0的情况写了出来,用到了exit(0),让程序遇到除0时直接结束。后来修修改改,第二个点也改了出来,因为漏掉了要入栈的字符优先级低时,出栈字符后要将该字符入栈,最后一个点是没有出栈彻底,只出栈一个元素就入栈。
题目2:7-8 jmu-ds-二叉树叶子结点带权路径长度和
设计思路(伪代码或流程图)
void CreateBTree(BTree &BT,string str,int i){
if(串中i位置的字符为#)
BT为空节点
else
BT申请空间,复制str[i]
左右孩子为空
if(2*i+1没超过串的长度,即还有左右孩子)
递归建BT的左孩子,串中位置2*i
递归建BT的右孩子,串中位置2*i+1
}//建树
void getwpl( BTree BT,int &wpl,int h ){
h第一次调用为0
if(BT不为空)
if(BT左右孩子都为空)//叶子节点
该点h*BT的权值累加到wpl
h归0
h++,计算路径长
if(BT为空)递归出口
递归调用计算BT左孩子wpl
递归调用计算BT右孩子wpl
}//计算wpl
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
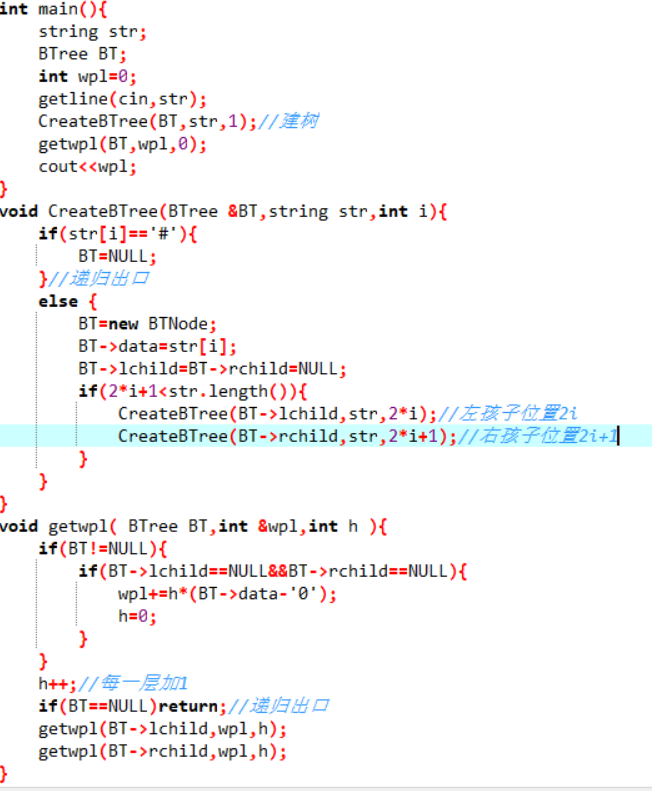
PTA提交列表说明。
开始自己有点想法写了一大堆非递归的操作,写到最后没一个点对,该了一下就只有空树时是对的,一下子不知道怎么写,于是就去请教了其他同学,他告诉我可以用递归的方法写一写,于是我自己写了建树的递归方法,代码简洁了很多,最后算wpl的函数是同学给我看了一下,理解后自己写了个差不多的,提交就对了。
题目3:7-7 修理牧场
设计思路(伪代码或流程图)
优先队列:会在入栈后自动将栈内元素进行排序,值比较大的排在栈底
建立优先队列
输入N和M
for i=0 to n-1
输入每块木头长,入栈
定义sum统计最后结果
while(栈不为空)
出栈两个元素相加
结果累加到num
num入栈
输出sum
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
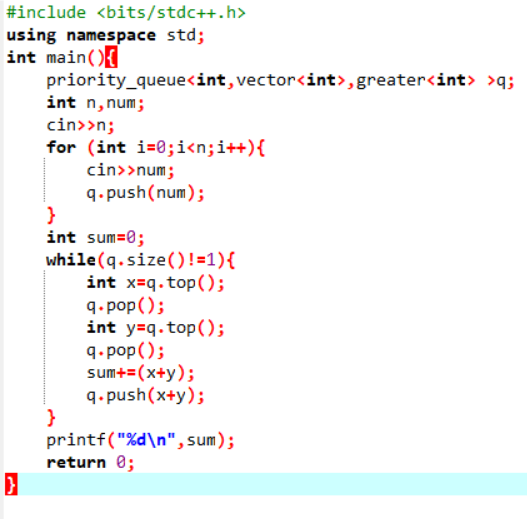
PTA提交列表说明。
先是用课本上哈夫曼树的方法,但是只有前面的两点正确,于是想起了老师说这道题的时间复杂度被严格限定,于是去百度了下优先队列,发现理解后发现这道题很简单。
3.截图本周题目集的PTA最后排名(3分)

3.1 PTA排名:4
3.2 我的得分:230
4. 阅读代码(必做,1分)
题目:帅到没朋友
当芸芸众生忙着在朋友圈中发照片的时候,总有一些人因为太帅而没有朋友。本题就要求你找出那些帅到没有朋友的人。
输入格式:
输入第一行给出一个正整数N(<=100),是已知朋友圈的个数;随后N行,每行首先给出一个正整数K(<=1000),为朋友圈中的人数,然后列出一个朋友圈内的所有人——为方便起见,每人对应一个ID号,为5位数字(从00000到99999),ID间以空格分隔;之后给出一个正整数M(<=10000),为待查询的人数;随后一行中列出M个待查询的ID,以空格分隔。
注意:没有朋友的人可以是根本没安装“朋友圈”,也可以是只有自己一个人在朋友圈的人。虽然有个别自恋狂会自己把自己反复加进朋友圈,但题目保证所有K超过1的朋友圈里都至少有2个不同的人。
输出格式:
按输入的顺序输出那些帅到没朋友的人。ID间用1个空格分隔,行的首尾不得有多余空格。如果没有人太帅,则输出“No one is handsome”。
注意:同一个人可以被查询多次,但只输出一次。
输入样例1:
3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
8
55555 44444 10000 88888 22222 11111 23333 88888
输出样例1:
10000 88888 23333
输入样例2:
3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
4
55555 44444 22222 11111
输出样例2:
No one is handsome
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int F[100005];
int visit[100005];
int Root[105];
int get_far(int x){
return F[x] == x ? x : F[x] = get_far(F[x]);
}
int Union(int x,int y){
int a = get_far(F[x]),b = get_far(F[y]);
if(a != b)
F[a] = b;
}
int main()
{
int n;
while(cin>>n){
for(int i = 0;i < 100005;i ++)
F[i] = i;
int len = 0;
while(n--){
int m,root;
scanf("%d%d",&m,&root);
for(int i = 1;i < m;i ++){
int temp;
scanf("%d",&temp);
Union(root,temp);
}
if(m != 1)
Root[len++] = get_far(F[root]);
}
int k;
cin>>k;
int flag = 0,ans = 0;
memset(visit,0,sizeof(visit));
for(int i = 1;i <= k;i ++){
int f;
scanf("%d",&f);
if(!visit[f]){
int ok = 0;
visit[f] = 1;
for(int j = 0;j < len;j ++)
if(get_far(F[f]) == Root[j])
ok = 1;
if(!ok){
if(flag) cout<<" ";
printf("%05d",f);
flag = 1;
ans = 1;
}
}
}
if(!ans)
cout<<"No one is handsome"<<endl;
else
cout<<endl;
}
return 0;
}
并差集的应用,功能如题目所示。
优点:巧妙运用并查集的方法,化繁杂的问题为简单的问题,就是用并查集将朋友圈的数据整合到一起,方便后序数据的查找。
5. 代码Git提交记录截图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号