小明年龄、成绩、名次的求解问题
1 问题的提出
小明的年龄、成绩、名次的成绩是2950,小明的名次、成绩是多少?
2 问题的假设
假设1:小明处于少年期(7~17岁),成绩为100分制。
假设2:不考虑“小”明还是“老”明,统一小明的年龄≥0岁且≤134岁(当前世界记录人类的最大年龄),成绩为100分制。
3 数学模型的描述
设小明的年龄为age,成绩为grade,名次为rank,因为年龄和名次均为整数,则成绩必为整数,考虑成绩是小数,例如92.5分是没有意义的,因此有以下数学模型。
4 数学模型的求解
该数学模型适合采用穷举法进行求解。
假设1下的求解。
MATLAB代码如下:
|
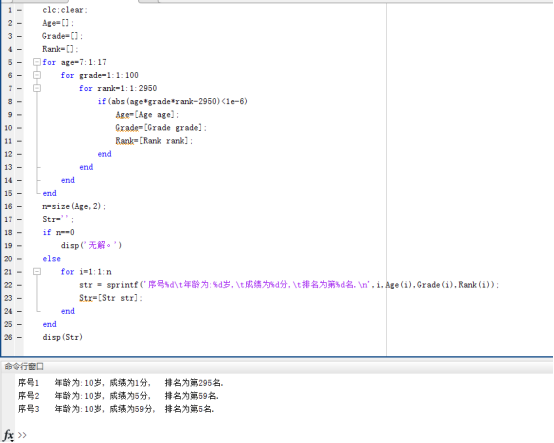
clc;clear; Age=[]; Grade=[]; Rank=[]; for age=7:1:17 for grade=1:1:100 for rank=1:1:2950 if(abs(age*grade*rank-2950)<1e-6) Age=[Age age]; Grade=[Grade grade]; Rank=[Rank rank]; end end end end n=size(Age,2); Str=''; if n==0 disp('无解。') else for i=1:1:n str = sprintf('年龄为:%d岁,\t成绩为%d分,\t排名为第%d名.\n',Age(i),Grade(i),Rank(i)); Str=[Str str]; end end disp(Str) |
运行求解结果如下:
|
序号1 年龄为:10岁, 成绩为1分, 排名为第295名. 序号2 年龄为:10岁, 成绩为5分, 排名为第59名. 序号3 年龄为:10岁, 成绩为59分, 排名为第5名. |
因此在假设1下有3个解:
小明年龄为:10岁,成绩为1分,排名为第295名或年龄为:10岁,成绩为5分,排名为第59名或年龄为:10岁,成绩为59分,排名为第5名。
假设2的求解。
仅需将上述代码中的age=7:1:17替换成age=1:1:134。
运行求解结果如下:
|
序号1 年龄为:1岁, 成绩为1分, 排名为第2950名. 序号2 年龄为:1岁, 成绩为2分, 排名为第1475名. 序号3 年龄为:1岁, 成绩为5分, 排名为第590名. 序号4 年龄为:1岁, 成绩为10分, 排名为第295名. 序号5 年龄为:1岁, 成绩为25分, 排名为第118名. 序号6 年龄为:1岁, 成绩为50分, 排名为第59名. 序号7 年龄为:1岁, 成绩为59分, 排名为第50名. 序号8 年龄为:2岁, 成绩为1分, 排名为第1475名. 序号9 年龄为:2岁, 成绩为5分, 排名为第295名. 序号10 年龄为:2岁, 成绩为25分, 排名为第59名. 序号11 年龄为:2岁, 成绩为59分, 排名为第25名. 序号12 年龄为:5岁, 成绩为1分, 排名为第590名. 序号13 年龄为:5岁, 成绩为2分, 排名为第295名. 序号14 年龄为:5岁, 成绩为5分, 排名为第118名. 序号15 年龄为:5岁, 成绩为10分, 排名为第59名. 序号16 年龄为:5岁, 成绩为59分, 排名为第10名. 序号17 年龄为:10岁, 成绩为1分, 排名为第295名. 序号18 年龄为:10岁, 成绩为5分, 排名为第59名. 序号19 年龄为:10岁, 成绩为59分, 排名为第5名. 序号20 年龄为:25岁, 成绩为1分, 排名为第118名. 序号21 年龄为:25岁, 成绩为2分, 排名为第59名. 序号22 年龄为:25岁, 成绩为59分, 排名为第2名. 序号23 年龄为:50岁, 成绩为1分, 排名为第59名. 序号24 年龄为:50岁, 成绩为59分, 排名为第1名. 序号25 年龄为:59岁, 成绩为1分, 排名为第50名. 序号26 年龄为:59岁, 成绩为2分, 排名为第25名. 序号27 年龄为:59岁, 成绩为5分, 排名为第10名. 序号28 年龄为:59岁, 成绩为10分, 排名为第5名. 序号29 年龄为:59岁, 成绩为25分, 排名为第2名. 序号30 年龄为:59岁, 成绩为50分, 排名为第1名. 序号31 年龄为:118岁, 成绩为1分, 排名为第25名. 序号32 年龄为:118岁, 成绩为5分, 排名为第5名. 序号33 年龄为:118岁, 成绩为25分, 排名为第1名. |
因此在假设2下有33个解。



