深度学习—序列分析初探

循环神经网络 (RNN)

       CNN等传统神经网络的局限在于：将固定大小的向量作为输入（比如一张图片），然后输出一个固定大小的向量（比如不同分类的概率）。不仅如此，CNN还按照固定的计算步骤（比如模型中层的数量）来实现这样的输入输出。这样的神经网络没有持久性：假设你希望对电影中每一帧的事件类型进行分类，传统的神经网络就没有办法使用电影中先前的事件推断后续的事件。所有就有了循环神经网络，他的本质是：像人一样拥有记忆的能力。因此，他的输出就依赖于当前的输入和记忆。

• RNN 是包含循环的网络，可以把信息从上一步传递到下一步。

• RNN允许信息的持久化，对当前的状态保留记忆（以隐变量的方式存在，也就是图中计算h_{t}需要用到h_{t-1}的信息）。对于同一个RNN来说，其“A结构”（绿色部分）是固定的（共享一套参数，毕竟是从循环展开来的啊肯定是一样的）。

A代表神经网络的一部分（传统CNN的A中只有一个非常简单的结构，例如图中的tanh层）。X_{t}代表t时刻的输入，h_{t}代表t时刻的输出。

• RNN允许人们对向量序列进行操作（无论是输入还是输出）。

RNN对向量序列的操作，红、绿、蓝矩形分别代表输入、“A结构”和输出，箭头代表向量f流向以及特定函数（矩阵乘法等等）

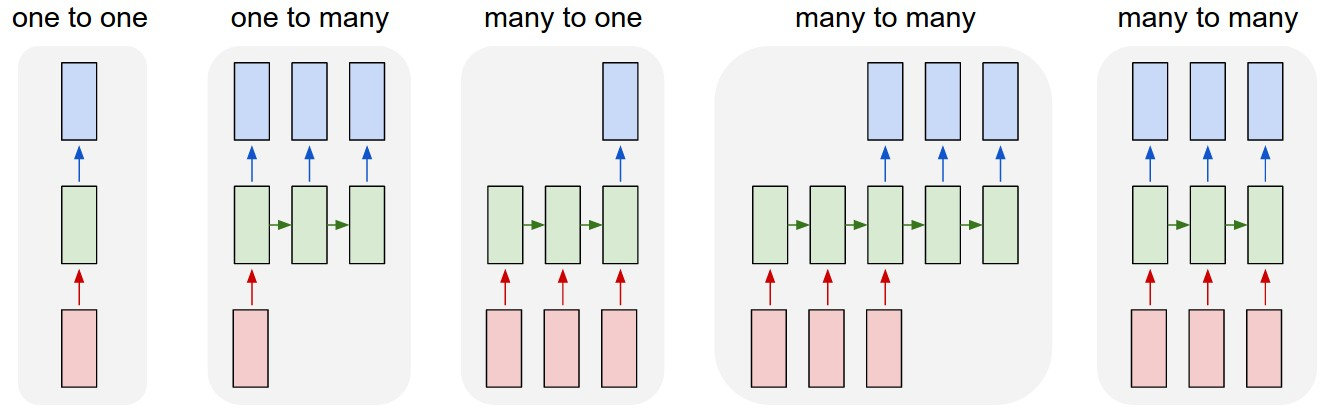
上图中的5个例子从左到右分别是：

1. 没有使用RNN，从固定大小的输入得到固定大小输出（比如图像分类）
2. 序列输出（比如图片描述，输入一张图片输出一段文字序列）
3. 序列输入（比如情感分析，输入一段文字然后将它分类成积极或者消极情感）
4. 序列输入和序列输出（比如机器翻译）
5. 同步序列输入输出（比如视频分类，对视频中每一帧打标签）

• 具体网络结构如下：

其中每个圆圈可以看作是一个单元，而且每个单元做的事情也是一样的，因此可以折叠呈左半图的样子。用一句话解释RNN，就是一个单元结构重复使用。

我们定义：Xt:表示t时刻的输入，ot:表示t时刻的输出，St:表示t时刻的记忆
St=f(U∗Xt+W∗St−1)，f()为激活函数，用来过滤之前的信息，可能为tanh，也可以为其他。
RNN预测输出是要带着当前时刻记忆St去预测，而且预测时也要对当前记忆St设置一个权重矩阵V，使得重要的部分发挥的作用最大，公式表达如下：ot=softmax(VSt)，其中ot就表示时刻t的输出。
RNN中的结构细节：
1.可以把St当作隐状态，拥有了之前时间点上的信息。
2.ot是由当前时间以及之前所有的记忆得到的。
3.但是，St并不能捕捉之前所有时间点的信息。
4.和卷积神经网络一样，这里的网络中每个cell都共享了一组参数（U，V，W）,这样就能极大的降低计算量了。
5.ot在很多情况下都是不存在的，因为很多任务，比如文本情感分析，都是只关注最后的结果的。

• RNN存在的问题：

1. 梯度消失问题：RNN中一般会用tanh()函数作为激活函数，而tanh函数如下图所示，在迭代后期，会逐渐收敛，导致梯度趋于0，于是，出现了“梯度下降”的问题。
2. 长期依赖问题：当前系统的状态，可能受很长时间之前系统状态的影响，是RNN中无法解决的一个问题。

 LSTM 网络

长短时记忆网络（LSTM）能够在一定程度上解决RNN存在的问题。

LSTMs 和RNN有相似的结构（唯一的区别就是中间部分）。但是它们不再只是用一个单一的 tanh 层，而是用了四个相互作用的层。

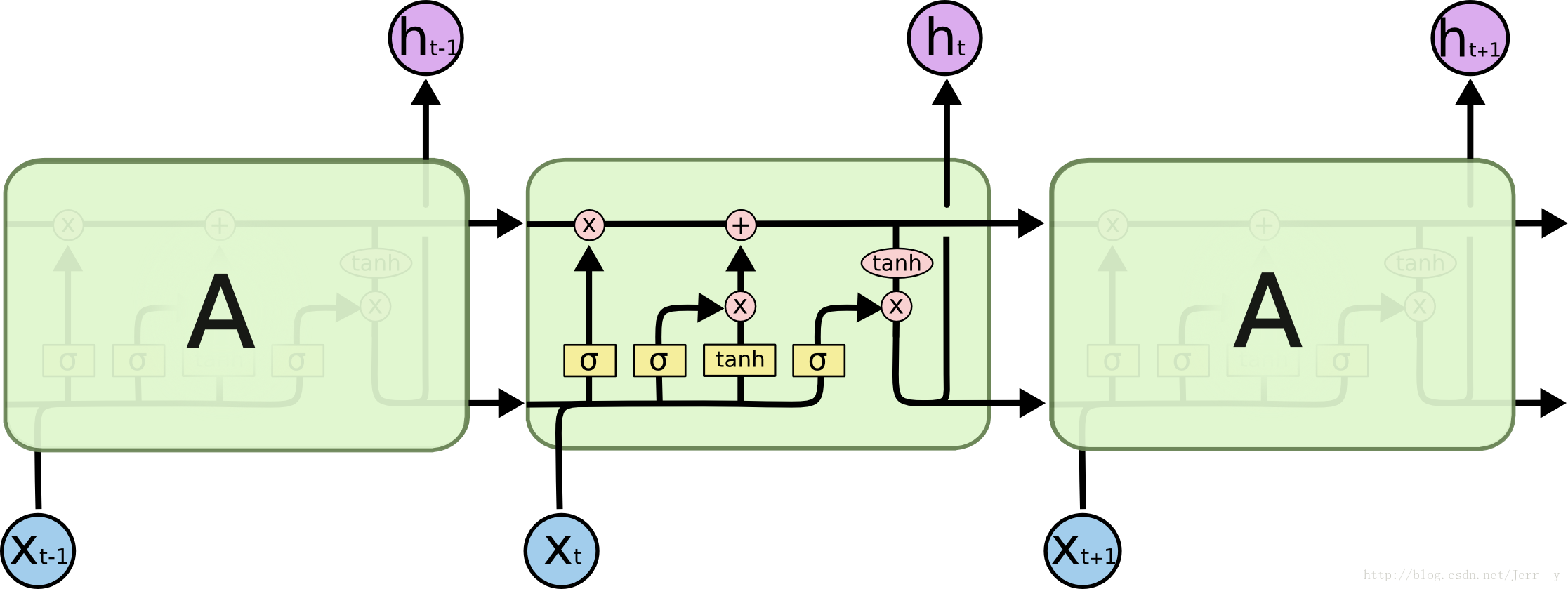
LSTMs 最关键的地方在于 cell（整个绿色的框就是一个 cell） 的状态 和 结构图上面的那条横穿的水平线，cell 状态的传输就像一条传送带，向量从整个 cell 中穿过，只是做了少量的线性操作。这种结构能够很轻松地实现信息从整个 cell 中穿过而不做改变。（这样我们就可以实现了长时期的记忆保留了）。

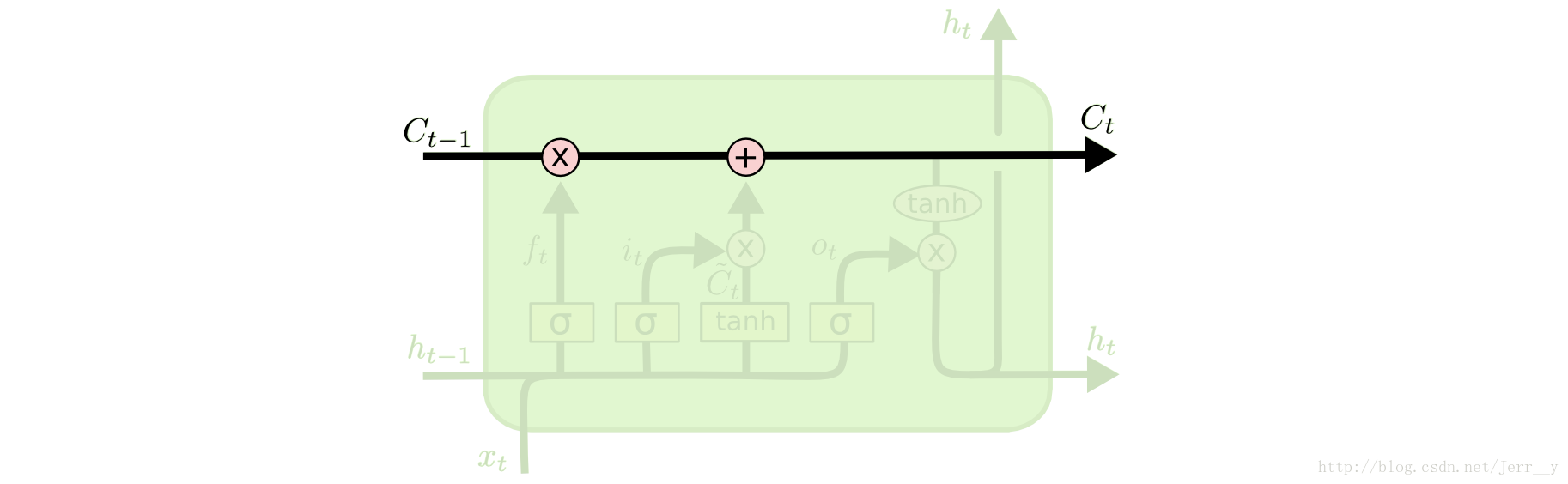
若只有上面的那条水平线是没办法实现添加或者删除信息的。而是通过一种叫做 门（gates） 的结构来实现的。

门 可以实现选择性地让信息通过，主要是通过一个 sigmoid 的神经层 和一个逐点相乘的操作来实现的。

sigmoid 层输出（是一个向量）的每个元素都是一个在 0 和 1 之间的实数，表示让对应信息通过的权重（或者占比）。比如， 0 表示“不让任何信息通过”， 1 表示“让所有信息通过”。

每个 LSTM 有三个这样的门结构，来实现保护和控制信息。（分别是 “forget gate layer”, 遗忘门； “input gate layer”，传入门； “output gate layer”, 输出门。

遗忘门

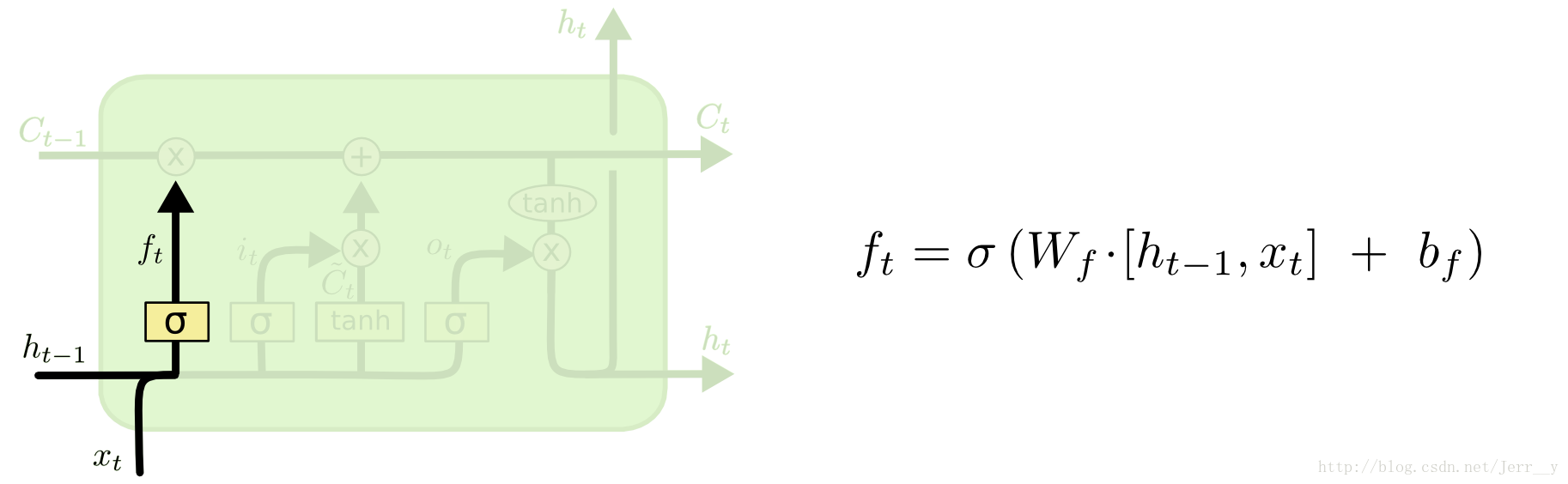
首先是 LSTM 要决定让那些信息继续通过这个 cell，这是通过一个叫做“forget gate layer ”的sigmoid 神经层来实现的。它的输入是$ h_{t-1} 和和和 x_t $，输出是一个数值都在 0，1 之间的向量（向量长度和 cell 的状态 $ C_{t-1} $ 一样），表示让 $C_{t-1} $ 的各部分信息通过的比重。 0 表示“不让任何信息通过”， 1 表示“让所有信息通过”。

 

传入门

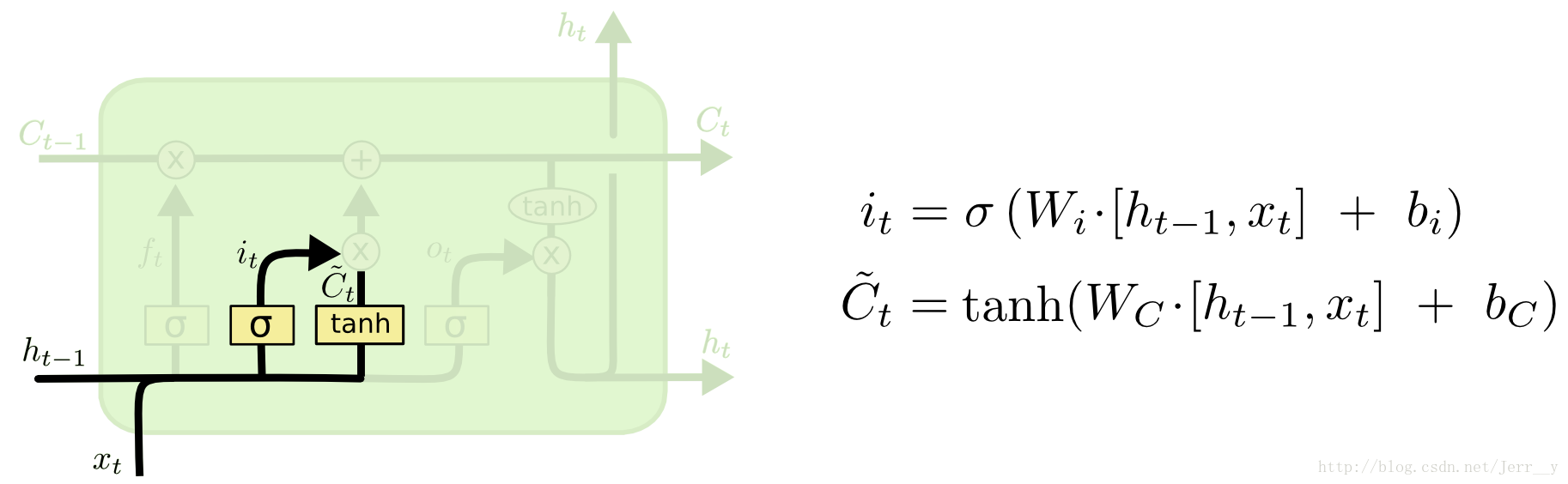
下一步是决定让多少新的信息加入到 cell 状态 中来。实现这个需要包括两个 步骤：首先，一个叫做“input gate layer ”的 sigmoid 层决定哪些信息需要更新；一个 tanh 层生成一个向量，也就是备选的用来更新的内容，Ct˜\tilde{C_t}Ct​~​ 。在下一步，我们把这两部分联合起来，对 cell 的状态进行一个更新。

 

 

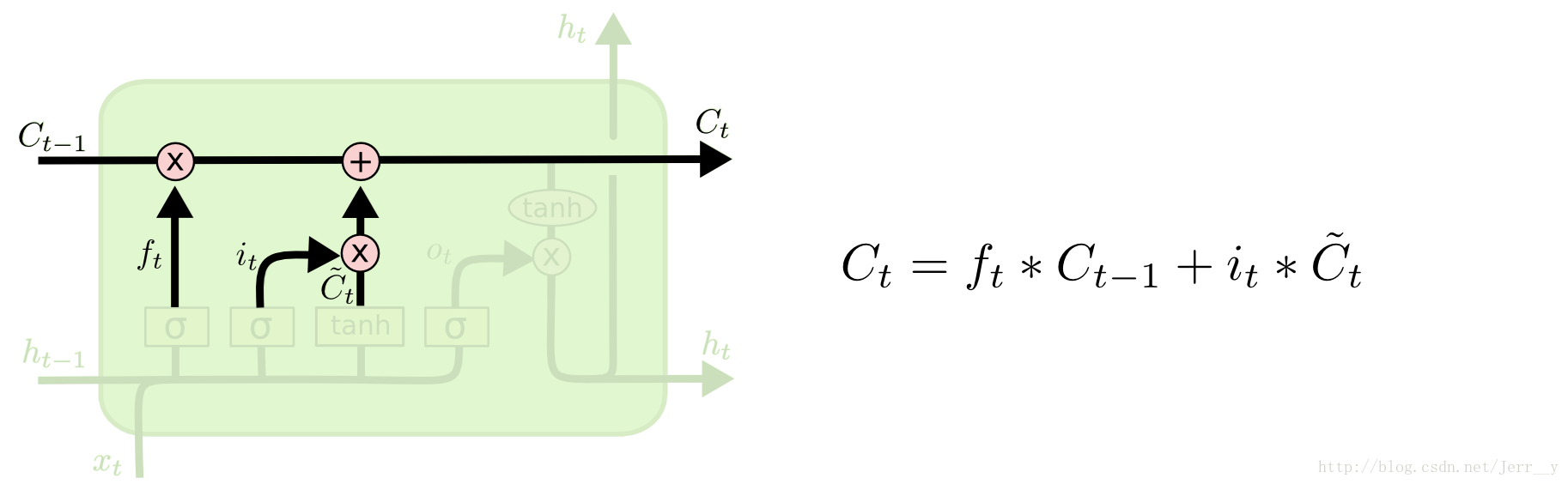
 输出门

 

最后，我们需要来决定输出什么值了。这个输出主要是依赖于 cell 的状态$ C_t$，但是又不仅仅依赖于 $C_t ，而是需要经过一个过滤的处理。首先，我们还是使用一个sigmoid层来（计算出）决定，而是需要经过一个过滤的处理。首先，我们还是使用一个 sigmoid 层来（计算出）决定，而是需要经过一个过滤的处理。首先，我们还是使用一个sigmoid层来（计算出）决定C_t 中的哪部分信息会被输出。接着，我们把中的哪部分信息会被输出。接着，我们把中的哪部分信息会被输出。接着，我们把 C_t $通过一个 tanh 层（把数值都归到 -1 和 1 之间），然后把 tanh 层的输出和 sigmoid 层计算出来的权重相乘，这样就得到了最后输出的结果。

 

原文链接： Understanding LSTM Networks

参考博客：https://www.cnblogs.com/DjangoBlog/p/7699537.html