解决LCS问题，需要把原问题分解成若干个子问题，所以需要刻画LCS的特征。
设A=“a0，a1，…，am”，B=“b0，b1，…，bn”，且Z=“z0，z1，…，zk”为它们的最长公共子序列。不难证明有以下性质：
如果am=bn，则zk=am=bn，且“z0，z1，…，z(k-1)”是“a0，a1，…，a(m-1)”和“b0，b1，…，b(n-1)”的一个最长公共子序列；
如果am!=bn，则若zk!=am，蕴涵“z0，z1，…，zk”是“a0，a1，…，a(m-1)”和“b0，b1，…，bn”的一个最长公共子序列；
如果am!=bn，则若zk!=bn，蕴涵“z0，z1，…，zk”是“a0，a1，…，am”和“b0，b1，…，b(n-1)”的一个最长公共子序列。
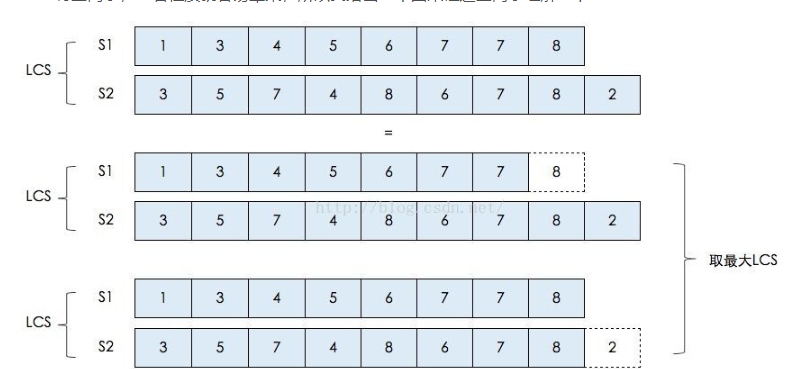
感谢这个博主，这意思是，求最长公共子序列，你肯定要比较A字串M个和B字串N个中的元素是否相同，那怎么记录呢，就想到用二维数组，但是你不能记录每一个是否相同吧，记为0和1的话太没用了，那怎么办，利用动态规划，前面比较过的，你可以拿来用啊，这就用到了递归思想，意思就是每次只比较A的B的最后一个，如果相同，则+1，并且记录寻找的路径，如果不同，就寻找减去最后一个元素的两种谁的公共子序列比较长，就选谁（比如呢，A的最后一个是不是没用了，那就比较A减去倒数第一个和B进行比较，但是还可能B在增长，那么就是B减去倒数第一个）在这里，我用二维数组c存有多少个公共子序列，b存寻找的方向，1代表斜着，2代表向上边，3代表左边
我们可以发现，假设我需要求 a1 ... am 和 b1 .. b(n-1)的LCS 和 a1 ... a(m-1) 和 b1 .. bn的LCS，一定会递归地并且重复地把如a1... a(m-1) 与 b1 ... b(n-1) 的 LCS 计算几次。所以我们需要一个数据结构来记录中间结果，避免重复计算。
假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度（直接保存最长公共子序列的中间结果不现实，需要先借助LCS的长度）。其中X = {x1 ... xm}，Y ={y1...yn}，Xi = {x1 ... xi}，Yj={y1... yj}。可得递归公式如下：
借用 https://blog.csdn.net/hrn1216/article/details/51534607 博主的图。
借用博主的图来说明
初始化为0，你发现这样，对于（1.1）就是1和3的比较，对于（1.2）就是A（1），B（3.5）的比较，然后依次，发现都为0，B依次增长，然后A增长，（2.1）就是A(1.3) B(3)的比较，诶，出现了，就是如图记录为坐标（2-1，1-0）的值+1，放入到(2.1)中，这意味着什么呢，就是A，B串各减去一，只留各自最后一个作比较，好了，如图
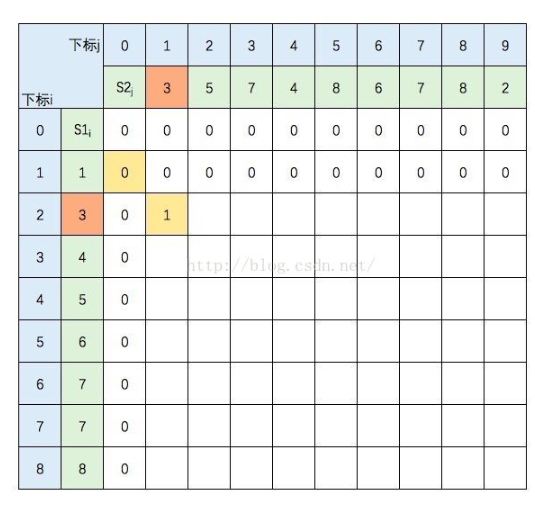
然后就是B递增，（2.2）就是A（1.3）和B（3.5）发现3和5不同，那就max吧，看是A减去最后一个的子串和B比较得出的公共子序列长呢还是B减去最后一个子串和A比较的公共子序列长呢。发现是（2.1）=1比较长，也就是A（1.3）和B（3），然后顺延咯
最后得出如图
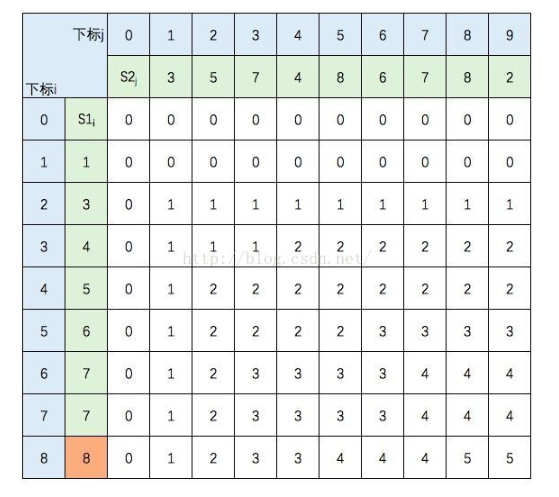
OK，下面贴出实现这个表格的代码
void LCSLength(int m, int n, char *x, char *y, int (*c)[15], int (*b)[15]) { int i, j; for (int i = 0; i <= m+1; i++) c[i][0] = 0; for (int i = 0; i <= n+1; i++) c[0][i] = 0; for (int i = 1; i<m+1; i++) for (int j = 1; j <= n+1; j++) { if (x[i] == y[j]) { c[i][j] = c[i - 1][j - 1] + 1; b[i][j] = 1; } else if (c[i - 1][j] >= c[i][j - 1]) { c[i][j] = c[i - 1][j]; b[i][j] = 2; } else { c[i][j] = c[i][j - 1]; b[i][j] = 3; } } }
初始化，然后遍历m*n的列表，
{
如果A和B串最后一个比较相同，+1
不然{
要么c（i-1，j）>c(i,j-1),则延续上边
}
不然{
要么c（i，j-1）>c(i-1,j),则延续左边
}
}
下面贴出寻找的代码，寻找是倒着寻找的，从二维数组的最后一个，到第（0.0），只有出现1，也就是很明显的A和B的最后一个相等，才会输出嘛，不然就意味这这俩不等，是延续上面的嘛。
void LCS(int i,int j, char *x, int (*b)[15]) { if (i == 0 || j == 0) return; if (b[i][j] == 1) { LCS(i - 1,j - 1, x, b); cout << x[i] << " "; } else if (b[i][j] == 2) LCS(i - 1, j, x, b); else LCS(i, j - 1, x, b); }
OK，下面就是主函数了，不做说明了，C++学得不好
int main() { cout << "请输入序列的长度" << endl; int m, n; cin >> m >> n; cout << "请输入公共子序列一" << endl; char x[100], y[100]; for (int i = 1; i <= m; i++) { cin >> x[i]; cout << x[i]; } for (int j = 1; j <= n; j++) cin >> y[j]; int c[15][15]; int b[15][15]; LCSLength(m, n, x, y, c,b); for (int i = 0; i < m+1; i++) { for (int j = 0; j < n+1; j++) { cout << c[i][j] << " "; } cout << endl; } LCS(m, n, x, b); system("pause"); }
