2018/8/9 MultiU 6 并查集+dfs,反向建边提高查询效率 ！！！ / 最大字段和n维（降维）/ 状压+中途相遇法

hdu6370 Werewolf

 

http://acm.hdu.edu.cn/showproblem.php?pid=6370

题意：村民只能说真话，狼人“可以”撒谎，每个人说一句话指向出自己之外任意一人身份，问与多少铁民和铁狼。

思路：1.因为可以有全狼的情况，所以不存在铁民。

           2.通过基环树找狼。（具体参见下图，搬运于别人的博客QAQ。。。）

 

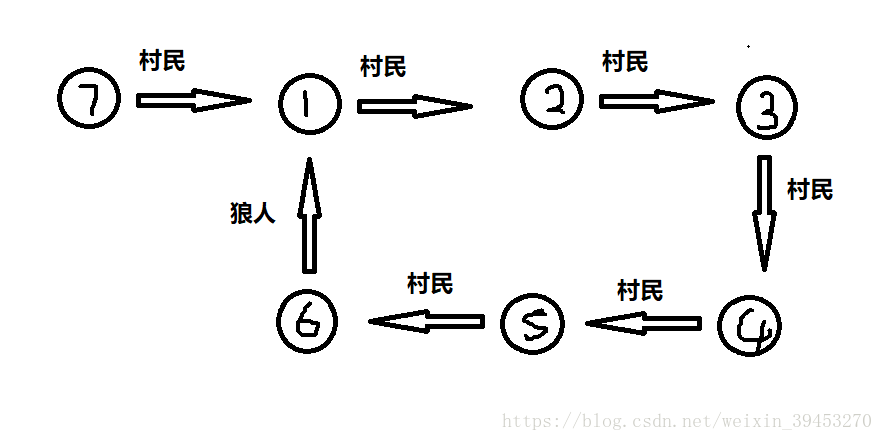
    当我们发现有连续个点是有村民的边，如点1，点2，点3，点4，点5，点6；而这些个连续的其中一个点（如图中的点6）有一条狼人边连到了这些个连续的其他的点（如上图连到了点1）。

    此时，我们用反证法可以证明，倘若1号点是村民，则根据村民不会说谎的性质可以判断出1到6号点全是村民，而根据村民不会说谎的性质，只能证明出1号点必为狼人。此时我们同时也可以发现，倘若1号点是狼人，则根据狼人会说谎的性质可知，指向1号点为村民的也必定是狼人。

    因此我们的算法雏形就初步显现出来了。

    我们要维护一些连续的村民点，可以用一个并查集进行维护。我们可以将村民边上的两个点不断的用并查集去合并，而当我们遍历狼边的时候，倘若我们发现狼边上的两个点都在一个集合中，则说明必定满足上述的情况，则我们不断遍历这条狼人边所指向的那个结点（如上图的1号点），判断有多少条指向它的村民边即可。（此处我们可以将村民边反向建立，这样可以让我们高效的查询）。

参考题解:https://blog.csdn.net/weixin_39453270/article/details/81515570

 

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+5;
typedef pair<int, int> pii;
vector<int> vi[N];
vector<pii>wolf;
int p[N],n;

void init(){
    for(int i=0;i<=n;i++) p[i]=i, vi[i].clear();
    wolf.clear();
}
int root(int x){
    while(p[x]!=x) x=p[x];
    return x;
}
bool same(int x, int y){
    return root(x) == root(y);
}
void unit(int x, int y){
    int tmp1 = root(x), tmp2 = root(y), cur;
    if(tmp1 == tmp2) return;
    p[tmp2] = tmp1;
    while(y != tmp1){
        cur = p[y];
        p[y] = tmp1;
        y = cur;
    }
}
int ans;
void dfs(int x){
    int sz = vi[x].size();
    for(int i = 0; i < sz; i++){
        ans++;
        dfs(vi[x][i]);
    }
}

int main()
{
    int t, x;
    char s[20];
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        init();
        for(int i = 1; i <= n; i++){
            scanf("%d %s", &x, s);
            if(s[0] == 'w'){
                wolf.push_back(make_pair(i, x));///inverse.
            }
            else{
                vi[x].push_back(i);
                unit(x, i);
            }
        }
        ans = 0;
        int sz = wolf.size();
        for(int i = 0; i < sz; i++){
            if(same(wolf[i].first, wolf[i].second)){
                ans++;
                dfs(wolf[i].second);
            }
        }
        printf("0 %d\n", ans);
    }
    return 0;
}

 打多校的几场下来，就是a完水题就挂机，然后赛后看题解，有的时候看完题解还是不知道该怎么写，于是看别人的代码，于是于是。。。依然啥也不会。。。（怨念。。o(一︿一+)o）

 

颓废度日，看底特律到睡着后决定补大白上的题然后。。。QAQ。。。lrj太强了!!!伏地膜！！！啊啊啊啊啊人家写出来的程序怎么这么xxxxxxx！！！x~

uva10755 G - Garbage Heap

题意:求解最大子“立方体”和。

思路:三位最大子段和，降维->二维，暴力枚举子矩阵O（n^4），第三维度采取最大子段和O(n)的dp解决，总复杂度O（n^5）。

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 20 + 5;
const ll inf = 1ll<<60;///
ll S[N][N][N];
int a, b, c, b0, b1, b2;

void expand(int i, int& b0, int& b1, int& b2){
    b0 = i&1; i >>= 1;
    b1 = i&1; i >>= 1;
    b2 = i&1;
}
int sign(int b0, int b1, int b2){ return (b0+b1+b2)&1? 1: -1;}

ll sum(int x1, int x2, int y1, int y2, int z1, int z2){
    int dx = x2-x1+1, dy = y2-y1+1, dz = z2-z1+1;
    ll s = 0;
    for(int i = 0; i < 8; i++){
        expand(i, b0, b1, b2);
        s -= S[x2-b0*dx][y2-b1*dy][z2-b2*dz] * sign(b0, b1, b2);
    }
    return s;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--){
        scanf("%d %d %d", &a, &b, &c);
        for(int i = 1; i <= a; i++) for(int j = 1; j <= b; j++) for(int k = 1; k <= c; k++) scanf("%lld", &S[i][j][k]);
        for(int x = 1; x <= a; x++){
            for(int y = 1; y <= b; y++){
                for(int z = 1; z <= c; z++){
                    for(int i = 1; i <= 7; i++){
                        expand(i, b0, b1, b2);
                        S[x][y][z] += S[x-b0][y-b1][z-b2] * sign(b0,b1,b2);
                    }
                }
            }
        }
        ll ans = -inf, s;///...
        for(int x1 = 1; x1 <= a; x1++){
            for(int x2 = x1; x2 <= a; x2++){
                for(int y1 = 1; y1 <= b; y1++){
                    for(int y2 = y1; y2 <= b; y2++){
                        ll M = 0;
                        for(int z = 1; z <= c; z++){
                            s = sum(x1, x2, y1, y2, 1, z);
                            ans = max(ans, s - M);
                            M = min(M, s);///M<=0~~~
                        }
                    }
                }
            }
        }
        printf("%lld\n", ans);
        if(t) puts("");///PE...
    }
    return 0;
}

学习了lrj 的程序，思路清晰，解法实用有效，很容易将问题推广到四维或更高维度的情形。

 

H - Jurassic Remains（UVALive - 2965）

题意：n（<=24    24/2=12可状压）个字符串，选尽量多个串使得每个大写字母（26个字母， 可状压）都出现偶数次。

思路：1.将每个串转化为二进制，出现偶数次即为该位xor后为0。

           2.将字符串集合划分为两个集合，也转化为二进制，则有AxorB=0 -> A = B。（A、B为两集合中所有二进制异或和）。

           3.对于每个A=B，找到包含字符串数目最多（二进制中1最多->bitcount最大）的集合，这些集合中bitcount最大的集合即为答案~

 

#include <bits/stdc++.h>
using namespace std;

const int N = 24;
int A[N];
map<int, int> table;
char s[1000];

int bitcount(int i){ return i == 0? 0: bitcount(i>>1) + (i&1);}

int main()
{
    int n, x;
    while(~scanf("%d", &n)){
        memset(A, 0, sizeof(A));
        table.clear();
        for(int i = 0; i < n; i++){
            scanf("%s", s);
            for(int j = 0; s[j]; j++) A[i] ^= (1<<(s[j]-'A'));
        }
        int n1 = n>>1;
        int n2 = n - n1, N1 = (1<<n1);
        for(int i = 0; i < N1; i++){
            x = 0;
            for(int j = 0; j < n1; j++) if(i & (1<<j)) x ^= A[j];
            if(!table[x] || (bitcount(table[x]) < bitcount(i))) table[x] = i;
        }
        int ans = 0, N2 = (1<<n2);
        for(int i = 0; i < N2; i++){
            x = 0;
            for(int j = 0; j < n2; j++) if(i & (1<<j)) x ^= A[j+n1];
            if(table[x] && bitcount(ans) < bitcount(i) + bitcount(table[x])) ans = (i<<n1)|table[x];///both | and ^ are right and fast~
        }
        printf("%d\n", bitcount(ans));
        for(int i = 0; i < n; i++) if(ans & (1<<i)) printf("%d ", i+1);
        puts("");
    }
    return 0;
}

 

emm...莫名喜欢状压（x）.