Problem of Precision

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 24 Accepted Submission(s): 20

Problem Description

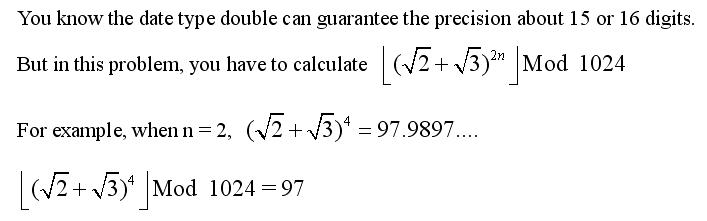Input

The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

Output

For each input case, you should output the answer in one line.

Sample Input

Sample Output

9
97
841

共轭数？？

网上是这么说的

我只是说一下推理过程

(m+n)^k=an+根号6bn

(m-n)^k=an-根号6bn

我们把上面的k次方展开，那么只有奇数次方（-n）^x(x属于奇数)才会对后面的产生影响，而影响加起来就是根号6bn (谢谢zhx～～)

 1 /*
 2 Author:wuhuajun
 3 */
 4 #include <cmath>
 5 #include <cstdio>
 6 #include <algorithm>
 7 #include <cstring>
 8 #include <string>
 9 #include <cstdlib>
10 using namespace std;
11 
12 typedef long long ll;
13 typedef double dd;
14 const int maxn=210,mod=1024;
15 
16 struct matrix
17 {
18    int m[3][3];
19 } ans,base,c;
20 int n,T,sum;
21 
22 void close()
23 {
24 
25 exit(0);
26 }
27 
28 matrix mul(matrix a,matrix b)
29 {
30    memset(c.m,0,sizeof(c.m));
31    for (int i=1;i<=2;i++)
32       for (int j=1;j<=2;j++)
33      for (int k=1;k<=2;k++)
34      {
35         c.m[i][j]+=a.m[i][k]*b.m[k][j];
36         c.m[i][j] %= mod;
37      }
38    return c;
39 }
40 
41 void work()
42 {
43    memset(ans.m,0,sizeof(ans.m));
44    ans.m[1][1]=ans.m[2][2]=1;
45    base.m[1][1]=5;
46    base.m[1][2]=12;
47    base.m[2][1]=2;
48    base.m[2][2]=5; 
49    n--;
50    while (n!=0)
51    {
52       if (n & 1)
53              ans=mul(base,ans);
54       n/=2;
55       base=mul(base,base);
56    }
57    sum=ans.m[1][1]*5+ans.m[1][2]*2;
58     sum*=2;
59     sum--;
60    sum %= mod;
61    printf("%d\n",sum);
62 }
63 
64 
65 void init()
66 {
67    scanf("%d",&T);
68    while (T--)
69    {
70       scanf("%d",&n);
71       work();
72    }
73 }
74 
75 int main ()
76 {
77    init();
78    close();
79    return 0;
80 }

posted on 2013-09-23 17:42 cssystem 阅读(223) 评论(0) 编辑收藏举报