线段树讲解
一、线段树概念及说明
线段树(Segment Tree):线段树是一种二叉搜索树,其最擅长的是进行区间处理操作,通常树上的每个节点都维护一个区间,线段树树根维护的是整个区间。每个子节点维护的是其父节点所维护区间二等分后的两个区间的其中之一。
线段树节点的结构如图1所示:
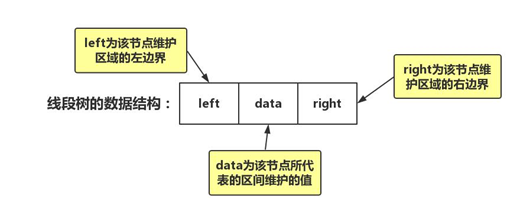
图1
给出一个【1~11】的区间,构建线段树,如图2所示:
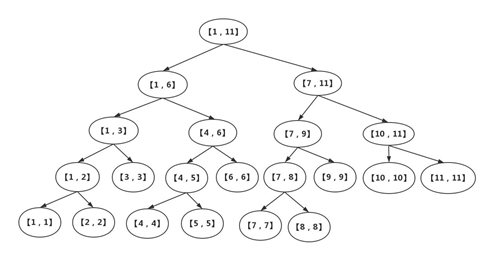
图2
通常构建【1~N】的线段树,我们需要开4*N的空间去构建,这是为什么?
在此对该结论不做理论性的证明,但是可以大概说一下原因。
首先对于[L,R]区间构建线段树,其中有N = R-L+1个整数,按照上面的方式构建线段树后,这样的一个区间,其节点数为2*N-1个,该结论也不做证明,但是你可以举例子去画树,会发现是满足这个结论的。
构建线段树其实就是建了一颗二叉树。对于二叉树,我们在学习数据结构的时候通常会介绍两种存储的方式:
第一种:链式存储。
第二种:顺序存储。
构建线段树的时候,我们通常采用的就是二叉树的第二种存储方式。二叉树的顺序存储结构就是用一组连续的地址连续的存储单元来存放二叉树数据元素。其基本方法是,对一颗二叉树中的节点进行从上到下从左到右的顺序依次从1开始对节点编号,假设每个节点都有两个孩子,则当某个节点编号为i的时候,其左孩子编号为2i,右孩子的编号为2i+1,我们根据二叉树节点的编号,把他们放置到数组中与他们编号相等的槽中,如果存在左孩子或右孩子不存在的情况,我们用特殊符号填充对应位置。这就是二叉树的顺序存储方法。例子如图3所示。
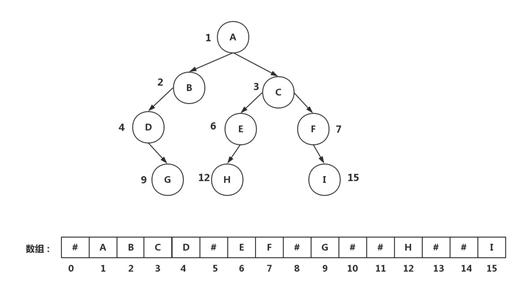
图3
从例子中这棵二叉树可以看出,虽然有些节点的左孩子或右孩子是空的,他们依旧占
据了一个存储空间,原因是存储的时候严格按照根、左、右编号给节点进行编号,而
线段树就是这样来存储的。刚才已经说过对于N个整数的区间,构建维护这个区间的线段树总共需要2N-1个节点,又因为根节点从数组下标为1的位置开始存储,那么至少需要的存储空间是2N,那么4N,多出的2N又是从哪里来的呢?
答案很简单,因为一些位置被空节点占据,就像给出的例子有些节点不存在,但是依然需要占据存储空间。如下面的这棵线段树图4:

图4
图中叶子节点分布在后两层,而倒数第二层的叶子节点其左右孩子不存在,但是会占据存储空间,原因是要编号到最后一个真实存在的节点,中间必然空6个位置,即图中6个空的节点。现在考虑最极限的情况,一个线段树维护【L,R】整个区间有N个整数,构建线段树后其层数有H层,假设第H-1层只有一个节点还能向下分解,并且该节点是第H-1层的最后一个节点,则由于已知最终叶子节点为N个,则第H-1层有N-2个叶子节点,由于H-1层一个非叶子节点在最后一个,导致前N-2个叶子节点的左右孩子虽然都是空,但是任然占据存储空间,二叉树真实存在的节点为2N-1个,在加上空节点占据的空间2(N-2).
2N-1 + 2(N-2) = 4*N - 5
这个是构建线段树时所占据的最极限的空间是4*N-5,所以通常我们开存储空间的时候就是开区间数字个数的4倍。
线段树的结构决定了我们在执行区间的操作的时候可以在O(logN)时间内完成,原因是其构树法则是根据二分的思想。
二、线段树的构建
1.如何实现线段树(递归方法)

从以上各图中可以看出,对于一个区间,如果其不是叶子节点,然后对其进行均等(此处均等的含义并非完全平均)拆分为左右节点,如果其左右孩子不是叶子节点,则继续拆分。从描述可以看出这是一个递归的过程(当然也可以转化为非递归过程)。这里代码以区间维护最大值为例:
const int maxn = 1e4;
int num[maxn]; ///各个位置上的数值
///线段树节点类型
typedef struct Node
{
int left;
int right;
int Max;
} node[maxn<<2]; ///范围扩 四倍
///构建线段树
void build(int root,int left,int right)
{
node[root].left = left;
node[root].right = right;
if(left == right)
{
node[root].Max = num[left];
return;
}
int mid = (left+right)>>1;
build(root<<1,left,mid);
build(root<<1|1,mid+1,right);
push_up(root); ///更新当前节点的函数。
}
push_up是更新当前节点的函数,如果节点维护的区间的最大值,则当前区间的最大值是其左右子区间中的最大值,如果节点维护的是区间和值,则父区间的值就是左右区间的和。
///维护区间最 值
void push_up(int root)
{
node[root].Max = max(node[root<<1].Max,node[root<<1|1].Max);
}
///维护区间的和值
void push_up(root)
{
node[root].sum = node[root<<1].sum + node[root<<1|1].sum;
}
例如给定数组 int num = {0,9,3,7,4,1,8,10}; 不带第一个数字0,总共有7个数字。构建线段树过程如图中箭头方向所示。
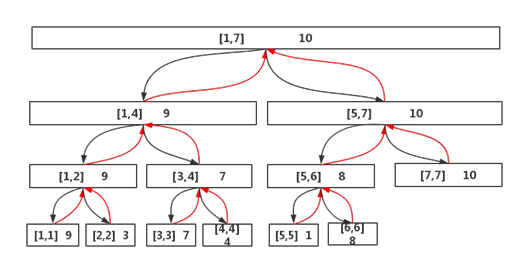
三、线段树单点更新,区间查询
1.单点更新
单点更新问题:把第pos位置上的值更新为value。
基本思路:把pos位置上的值更新为value,其过程和二分查找是一样的,对于当前区间【L,R】如果pos<=mid,则说明第pos个位置在左区间,否则说明第pos个位置在右区间,直到找到的区间是叶子节点,则说明找到了维护第pos个位置的叶子节点,则进行更新操作即可。
对于上图的线段树,加入需要把num数组中下标为3的位置改成12。
则执行如图操作。

更新操作代码:
///单点更新操作,把原来数组中的pos位置上的数字更新成value。
void update(int pos,int value,int root)
{
///是叶 节点
if(node[root].left == node[root].right)
{
node[root].Max = value; ///更新对应节点的值返回
return;
}
int mid = (left+right)>>1;
if(pos <= mid) update(pos,value,root<<1); ///节点位于左区间
else update(pos,value,root<<1|1); ///节点位于右区间
push_up(root); /// 节点更新后,更新 节点。
}
2.区间查询
区间查询是线段树中的一个重要操作,区间查询,给出【L,R】的区间,让你查询该区间所维护的。查询区间时候如果细分分为下面三种情况。设当前节点维护区间为[left,right],查询【L,R】内的值。我们做如下的处理。
1.如果R<=mid,则说明欲查询的区间【L,R】整个都在该区间的左侧,则只需要查询其左子树。
2.如果L>mid,则说明欲查询的区间【L,R】整个都在该区间的右侧,则只需要查询其右子树。
3.除1,2两种情况外,说明【L,R】横跨当前节点的左右区间,此时我们讲整个查询区间拆分为两部分别查询,即分为【L,mid】,[mid+1,R]分别进入左右子树进行查询操作。
例如还是针对上个树,我要查询【4,6】内的最大值,其过程如下图所示。

区间查询代码:
//查询【L,R】区间内的最 值。
int query(int L,int R,int root)
{
if(L==node[root].left && R==node[root].right)
{
return node[root].Max
}
int mid = (node[root].left+node[root].right)>>1;
int ans = 0;
if(R<=mid) //整个区间在当前区间的左 区间
ans = query(L,R,root<<1);
else if(L>mid) //整个区间在当前区间的右 区间
ans = query(L,R,root<<1|1);
else
{
//横跨区间的左右部分,查询区间[L,R]被拆分为[L,mid] 并上 [mid+1,R]
ans = query(L,mid,root<<1);
//查询左区间
ans = max(ans,query(mid+1,R,root<<1|1));
//查询右区间,并取 者最 值
}
return ans;
}
例题:HDU 1166 敌兵布阵
题目描述:
给出一个数T,代表有T组测试数据。
给出一个数N,表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2) Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3) Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4) End 表示结束,这条命令在每组数据最后出现;每组数据最多有40000条命令。
Simple IN
1 10
1 2 3 4 5 6 7 8 9 10 Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Simple out
Case 1:
6
33
59
解题思路:这个题目考察的就是线段树的单点更新和区间查询操作。
该题目中线段树的每个节点维护的一个区间的和值,因此在构建线段树的时候,当前区间的和值是左右区间的和。
当执行Add操作的时候,将第i个位置上的数字加上j,则我们按照二分查找的方法先找到这个节点,然后给节点的值加上j。当执行Sub操作的时候道理一样。当执行查询操作的时候就是线段树的普通查询。
代码:
#include<stdio.h>
#include<string.h>
#define lchild left,mid,root<<1 //左区间参数
#define rchild mid+1,right,root<<1|1 //右区间参数
const int maxn=50010;
int sum[maxn<<2];
void Push_Up(int root) //更新当前节点
{
sum[root] = sum[root<<1]+sum[root<<1|1];
}
//递归构建线段树
void Build(int left,int right,int root)
{
if(left == right) //左右边界 样
{
scanf("%d",&sum[root]); //输 节点的 兵数
return;
}
int mid = (left+right)>>1;
//递归构建左区间
//递归构建右区间
Build(lchild);
Build(rchild);
Push_Up(root); //计算left~right这个区间的 兵数量
}
//当Add或Sub i,j的时候更新值,更新 标节点的值在更新他所在区间的值。
void Update(int left,int right,int root,int target,int add)
{
if(left == right)
{
sum[root] += add;
return;
}
int mid = (left+right)>>1;
if(target<=mid) Update(lchild,target,add); //说明这点在左区间
else Update(rchild,target,add); //说明这点在右区间
//处理完root的左右区间,更新当前节点的值
Push_Up(root);
}
//区间查询,查询区间(L,R)之间的所有 兵
int Query(int L,int R,int left,int right,int root)
{
//当前节点的区间在所查询的区间之内,返回区间和值
if(L<=left && right<=R)
{
return sum[root];
}
int ans = 0;
int mid = (left+right)>>1;
//要查询的区间的右边界 于mid,说明要查询的区间位于当前节点的左区间
if(R<=mid) ans += Query(L,R,lchild);
else if(L>mid) ans += Query(L,R,rchild);
else
{
ans += Query(L,R,lchild);
ans += Query(L,R,rchild);
}
return ans;
}
int main()
{
int T,n,t=0,i,j;
scanf("%d",&T); //T组测试数据
while(T--)
{
printf("Case %d:\n",++t);
scanf("%d",&n);
Build(1,n,1);
while(1)
{
char str[50];
scanf("%s",str);
if(!strcmp(str,"End")) break;
else
{
scanf("%d%d",&i,&j);
if(!strcmp(str,"Add"))
{
Update(1,n,1,i,j);
}
else if(!strcmp(str,"Sub"))
{
Update(1,n,1,i,-j);
}
else
{
int ans = Query(i,j,1,n,1);
printf("%d\n",ans);
}
}
}
}
return 0;
}
四、线段树区间更新,区间查询
1.区间更新
区间更新就是给出【L,R】,对【L,R】这个区间中的每个数都进行同一种操作,例如将区间【L,R】中的每个数字都加上add。
在此将区间更新操作,以线段树区间求和为例。
假如在区间【L,R】间的每个数都加上add,首先我们可以知道【L,R】区间中总共有R-L+1个数,则每个数都加上add的时候,该区间的和值加上了(R-L+1)*add,对于区间更新我们通常并非会将所有在【L,R】范围内的节点全部更新,如果这样做在更新的时候通常就要深入到叶子节点,这样增加了时间复杂度,我们通常采用的做法是对线段树中的每个节点添加上标记lazy,在进行区间更新的时候,如果发现【L,R】的子区间我们更新当前节点的和值,同时将标记留下,该标记为该区间要加上的数字的总和。
为什么我们不直接在更新时将标记下推一步到位?
对于线段树来说区间更新、区间查询都是常见操作,如果对某个区间更新,但是后续或许我们的查询并不会用到那些被更新的区间,这时我们如果在区间更新的时候就费心将【L,R】的所有子区间都更新成正确的值,完全是在浪费时间,如果我们在查询过程中用来的这些区间,也必然会在递归的过程中到达这些区间,我们完全可以在查询的过程中边下推标记边查询,则此时更新时的下推也该操作重复,浪费时间。因此通常更新操作仅仅更新【L,R】下最靠上的子区间,并把标记留下,这个标记通常存在lazy数组中,叫做懒惰标记,然后在区间查询的过程中,由于区间查询时必须保证节点的数值正确,因此在区间查询的时候,我们用到那个节点,如果发现该节点有标记,则说明其子节点没有得到更新,此时我们下推标记,把标记推给它的左右孩子,没有发现标记的话则说明该节点左右孩子值正确。但是在更新过程中,发现有以前更新时留下的标记,也时需要下推的,而本次更新的标记则是点到为止。
加上lazy标记后,线段树的节点类型变成下面的结构:
const int maxn = 1e5;
typedef struct Node
{
int left; //节点所维护区间的左边界
int right; //节点所维护区间的右边界
int data; //节点的数据
int lazy; //节点的懒惰标记
} node[maxn<<2];
例如下面这棵线段树,我们在【1,6】区间给每个数字都加上3.如下图所示。
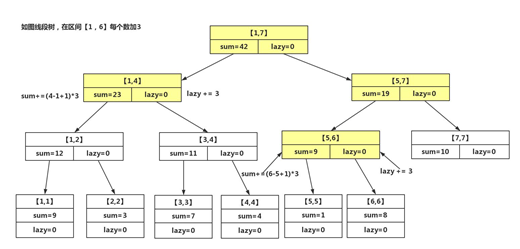
该树更新后如下图所示。
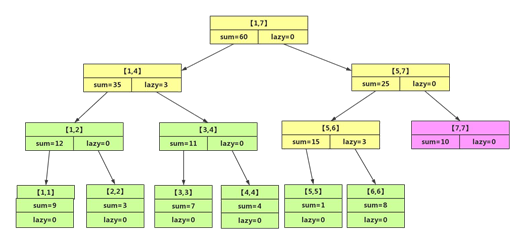
从图中可以看出黄色节点和粉色节点的值都是正确的,黄色节点是已经更新了值的节点,粉色节点并不在更新操作的区域内,其值也正确,而绿色节点属于黄色节点的子节点,由于标记没有下推,其值正确,在该图基础在区间【3,6】上加4,如下图所示。
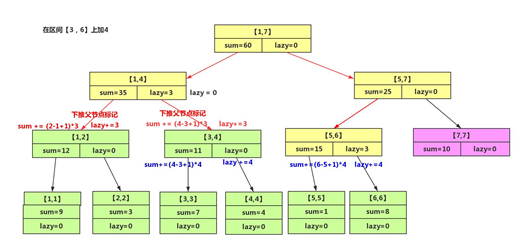
图中红色字体代表之前的标记下推,而蓝色字体代表当前更新操作。该操作完成后如下图所示。
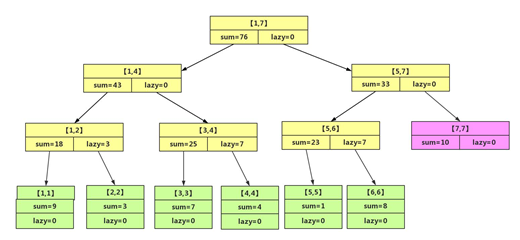
//更新当前节点
void push_up(int root)
{
node[root].sum = node[root<<1].sum + node[root<<1|1].sum;
}
//下推标记
void push_down(int root)
{
//说明该节点有标记
if(node[root].lazy>0)
{
//求左区间的 度
int leftLen = node[root<<1].right - node[root<<1].left + 1;
//求右区间的 度
int rightLen = node[root<<1|1].right - node[root<<1|1].left + 1;
//更新左区间和值
node[root<<1].sum += leftLen*node[root].lazy;
//更新右区间和值
node[root<<1|1].sum += rightLen*node[root].lazy;
//下推标记到左区间
node[root<<1].lazy += node[root].lazy;
//下推标记到右区间
node[root<<1|1].lazy += node[root].lazy;
//当前节点标记下推完毕,恢复成 标记状态
node[root].lazy = 0;
}
}
//将区[L,R]中的数字都加上add
void update(int L,int R,int add,int root)
{
//到达 区间,更新该区间的值,并留下标记
if(L<=node[root],left && node[root].right<=R)
{
node[root].sum += (node[root].right-node[root].left+1)*add;
node[root].lazy += add;
return;
}
push_down(root); //下推之前残留的标记
int mid = (node[root].left+node[root].right)/2;
if(L<=mid) update(L,R,add,root<<1); //更新左区间
if(R>mid) update(L,R,add,root<<1|1); //更新右区间
push_up(root); //更新当前节点
}
2.区间查询
和区间更新的步骤类似,如果所查询的区间有标记则下推,保证其查询区间的值是正确的,然后就和单点更新区间查询的过程是一样的。在此不在赘述。
//更新当前节点
void push_up(int root)
{
node[root].sum = node[root<<1].sum + node[root<<1|1].sum;
}
//下推标记
void push_down(int root)
{
//说明该节点有标记
if(node[root].lazy>0)
{
//求左区间的 度
int leftLen = node[root<<1].right - node[root<<1].left + 1;
//求右区间的 度
int rightLen = node[root<<1|1].right - node[root<<1|1].left + 1;
//更新左区间和值
node[root<<1].sum += leftLen*node[root].lazy;
//更新右区间和值
node[root<<1|1].sum += rightLen*node[root].lazy;
//下推标记到左区间
node[root<<1].lazy += node[root].lazy;
//下推标记到右区间
node[root<<1|1].lazy += node[root].lazy;
//当前节点标记下推完毕,恢复成 标记状态
node[root].lazy = 0;
}
}
int query(int L,int R,int root)
{
if(L<=node[root].left && node[root].right<=R)
{
return node[root].sum;
}
push_down(root); //下推残留标记
int mid = (node[root].left+node[root].right)/2;
int ans = 0;
if(L<=mid) ans += query(L,R,root<<1);
if(R>mid) ans += query(L,R,root<<1|1);
return ans;
}
例题:POJ 3468 A Simple Prolem With Integer 题目描述:
给出N个数字,Q次操作。
第二行给出N个数字的值。
接下来Q行,给出Q次操作,操作分为2种。
C a b c 给【a,b]中每个数字都加上c。 Q a b 查询[a,b]区间的和值。
解题思路:
区间更新、区间查询模板题目,该题线段树中每个节点维护的是区间的和,执行第一种操作,就直接用区间更新操作更新相应区间的值,执行第
二种操作,就直接用区间查询操作求解。输入:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出:
4
55
9
15
代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#define lchild left,mid,root<<1
#define rchild mid+1,right,root<<1|1
using namespace std;
const int maxn = 200000;
long long sum[maxn<<2];
long long lazy[maxn<<2];
void push_up(int root)
{
sum[root] = sum[root<<1] + sum[root<<1|1];
}
void push_down(int left,int right,int root)
{
if(lazy[root])
{
//下推标记
lazy[root<<1] += lazy[root];
lazy[root<<1|1] += lazy[root];
int mid = (left+right)>>1;
int leftlen = mid-left+1;
int rightlen = right-mid;
sum[root<<1] += lazy[root]*leftlen;
sum[root<<1|1] += lazy[root]*rightlen;
lazy[root] = 0;
}
}
void build(int left,int right,int root)
{
lazy[root] = 0;
if(left == right)
{
return;
}
int mid = (left+right)>>1;
build(lchild);
build(rchild);
push_up(root);
}
long long query(int L,int R,int left,int right,int root)
{
if(L<=left && right<=R)
{
return sum[root];
}
push_down(left,right,root); ///每次查询前先下推标记
int mid = (left+right)>>1;
long long ans = 0;
if(L<=mid) ans += query(L,R,lchild);
if(R>mid) ans += query(L,R,rchild);
return ans;
}
void update(int L,int R,int add,int left,int right,int root)
{
///到达 区间,修改节点值并留下标记
if(L<=left && right<=R)
{
sum[root] += (right-left+1)*add;
lazy[root] += add;
return;
}
push_down(left,right,root); //每次都先下推标记
int mid = (left+right)>>1;
if(L<=mid) update(L,R,add,lchild); //递归更新左 树
if(R>mid) update(L,R,add,rchild); //递归更新右 树
push_up(root); //更新当前节点
}
int main()
{
int N,Q;
while(~scanf("%d%d",&N,&Q))
{
memset(sum,0,sizeof(sum));
build(1,N,1); ///构建线段树
char op;
int L,R,C;
long long ans;
while(Q--)
{
scanf(" %c",&op);
if(op == 'Q')
{
scanf("%d%d",&L,&R);
ans = query(L,R,1,N,1);
printf("%lld\n",ans);
}
else
{
scanf("%d%d%d",&L,&R,&C);
update(L,R,C,1,N,1);
}
}
}
return 0;
}
五、线段树区间合并
线段树的区间合并是在上面基础上而扩展出来的一类题目,区间合并就是涉及到将区间合并成一个区间。
其题目的类型也比较多,题目对区间合并时的要求也不尽相同。
例题:CDOJ 360:Another LCIS
题目描述:
给出N个数字和Q次操作。(区间更新+区间合并)
如果操作类型是A,L, R,V 则在区间【L,R】上加上V,另外一种操作是查询【L,R】区间中最长连续递增子序列的长度。
对于操作A,给【L,R】内的值加上V,并不会对该区间的最长连续递增子序列造成影响,但是会给其父区间造成影响,因为其父区间是由子区间合并得来的。对于一个区间,其连续递增子序列的分布可以分为下面三种情况。
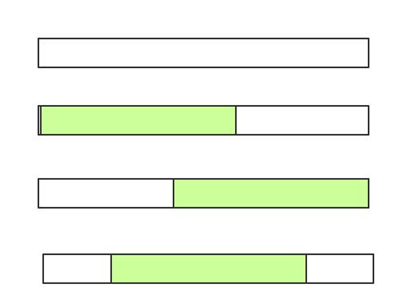
该题目线段树节点维护的值比较多。
Max 维护区间最长连续递增子序列的长度。
lnum 保留区间左边界位置的值。
rnum 保留区间右边界位置的值
lsum 以该区间左边界为开始的最长连续递增子序列的长度。
rsum 以该区间右边界为结束的最长连续递增子序列的长度。
当区间进行合并的时候,由于我们需要比较两个子区间相邻边界值的大小,则每个节
点必须保留左右边界的值,又由于需要根据边界大小,需要对区间进行合并,所以也
需要维护lsum,rsum这两个变量。
每次我们都要用子区间去更新父区间。
更新MAX:
1.不考虑区间拼接问题,则父区间的最长连续递增子序列是其左子区间和右子区间中最长的。
2.考虑拼接问题,如果左区间的右边界值比右区间的左边界值小,则区间可以合并,以左区间右边界为结尾的最长连续递增子序列长度+以右区间左边界值为开始的最长连续递增子序列长度。
两种情形如下图所示:
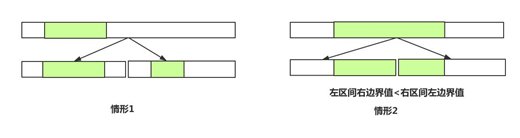
更新lnum,rnum:
父区间的左边界值为其左子区间左边界子,父区间右边界值为其右子区间边界值。这个很好理解
更新lsum,rsum:
1.不考虑区间拼接,父区间lsum,应该继承左子区间的lsum。
2.考虑区间拼接,如果左子区间和右子区间可以进行拼接,则如果左子区间整个区间都是递增的,则可以和右子区间的lsum拼接起来,形成父区间的lsum.
3.不考虑区间拼接,父区间rsum,应该继承右子区间的rsum.
4.考虑区间拼接,如果两个子区间可以进行拼接,则如果真个右子区间是递增的,则可以和左子区间的rsum拼接起来,形成父区间的rsum.
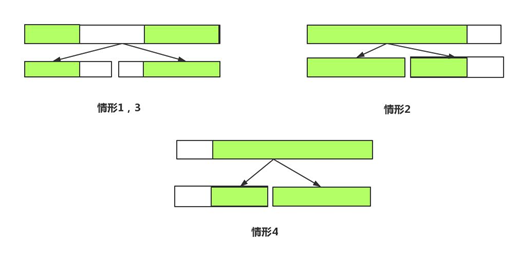
代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define lchild left,mid,root<<1
#define rchild mid+1,right,root<<1|1
using namespace std;
const int maxn = 100010;
int lsum[maxn<<2],rsum[maxn<<2],Max[maxn<<2],lazy[maxn<<2];
long long lnum[maxn<<2],rnum[maxn<<2];
///更新当前节点的值
void push_up(int left,int right,int root)
{
lnum[root] = lnum[root<<1]; ///区间的左边界是其左区间的左边界
rnum[root] = rnum[root<<1|1]; ///区间的有边界是其右区间的右边界
lsum[root] = lsum[root<<1]; ///以左端点为开始的连续递增序列 度是其左区间以左边界开始的连续递增序列 度
rsum[root] = rsum[root<<1|1]; ///以右断电为结束的连续递增序列 度是其右区间以有边界结束的连续递增序列 度
Max[root] = max(Max[root<<1],Max[root<<1|1]);
long long leftright = rnum[root<<1]; ///左区间的右侧数字 long long rightleft = lnum[root<<1|1]; ///右区间的左侧数字
int mid = (left+right)>>1;
///两个区间可能拼接在 起。
if(leftright<rightleft)
{
if(lsum[root] == mid-left+1)
{
lsum[root] += lsum[root<<1|1];
}
if(rsum[root] == right-mid)
{
rsum[root] += rsum[root<<1];
}
Max[root] = max(Max[root],rsum[root<<1]+lsum[root<<1|1]);
}
}
void push_down(int root)
{
if(lazy[root])
{
lazy[root<<1] += lazy[root];
lazy[root<<1|1] += lazy[root];
lnum[root<<1] += lazy[root];
rnum[root<<1] += lazy[root];
lnum[root<<1|1] += lazy[root];
rnum[root<<1|1] += lazy[root];
lazy[root] = 0;
}
}
void build(int left,int right,int root)
{
lazy[root] = 0;
if(left == right)
{
scanf("%lld",&lnum[root]);
rnum[root] = lnum[root];
Max[root] = lsum[root] = rsum[root] = 1;
return;
}
int mid = (left+right)>>1;
build(lchild);
build(rchild);
push_up(left,right,root);
}
void update(int L,int R,int add,int left,int right,int root)
{
if(L<=left && right<=R)
{
lnum[root] += add;
rnum[root] += add;
lazy[root] += add;
return;
}
push_down(root);
int mid = (left+right)>>1;
if(L<=mid) update(L,R,add,lchild);
if(R>mid) update(L,R,add,rchild);
push_up(left,right,root);
}
int query(int L,int R,int left,int right,int root)
{
if(L<=left && right<=R)
{
return Max[root];
}
push_down(root);
int ans = 1;
int mid = (left+right)>>1;
if(L<=mid) ans = max(ans,query(L,R,lchild));
if(R>mid) ans = max(ans,query(L,R,rchild));
if(rnum[root<<1] < lnum[root<<1|1])
{
ans = max(ans,min(R,mid+lsum[root<<1|1])-max(L,mid-rsum[root<<1]+1)+1);
}
return ans;
}
int main()
{
int T,Case=0;
scanf("%d",&T); ///T组测试数据
while(T--)
{
int N,Q;
scanf("%d%d",&N,&Q); ///N个数字,Q次操作
build(1,N,1);
char op;
int L,R,V;
printf("Case #%d:\n",++Case);
while(Q--)
{
scanf(" %c",&op);
if(op == 'a')
{
scanf("%d%d%d",&L,&R,&V);
update(L,R,V,1,N,1);
}
else
{
scanf("%d%d",&L,&R);
int ans = query(L,R,1,N,1);
printf("%d\n",ans);
}
}
}
return 0;
}
六、二维线段树(树套树的一种)
树套树,是一大类问题:有线段树套线段树,线段树套树状数组,主席树套线段树等等。在此只讲解简单的线段树套线段树,二维线段树。
有的时候,我们可能会用两个条件来维护一个值,要求查询X在【a,b】区间,Y在【c,d】区间内所能获得的值,这是我们常常将X,Y分别作为2维的其中一维,二维数组的每个格子作为需要维护的值。和普通一维线段树情况差不多,只不过相应的操作大部分需要写两遍。
例题:HDU 1832:Luck and Love
题目描述:
C个操作,如果操作符为‘I’,将H(身高),A(活跃度),L(缘分值)插入到二维线段树。
操作符为‘Q’,查询身高在【H1,H2】,活泼度在【A1,A2】中的最大缘分值。
解题思路:
线段树一维作为维护身高,二维维护活跃度,二维数组的值为缘分值。
代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define lchild left,mid,root<<1
#define rchild mid+1,right,root<<1|1
using namespace std;
const int maxm = 210; /// 维 个 代表 区域
const int maxn = 1010; /// 维 个列代表活跃度区域
int a[maxm<<2][maxn<<2]; ///整个数组维护的是缘分值 int M;
void push_up(int row,int root)
{
a[row][root] = max(a[row][root<<1],a[row][root<<1|1]);
}
void insert2(int row,int active,int love,int left,int right,int root)
{
if(left == right) ///到了叶 节点
{
///这 注意,可能插 两条相同的记录,避免 值覆盖 值 a[row][root] = max(a[row][root],love); return;
}
int mid = (left+right)>>1;
///递归插 左 树
if(active<=mid) insert2(row,active,love,lchild);
else insert2(row,active,love,rchild);
///递归插 右 树
///更新当前节点的最 值
push_up(row,root);
}
void insert1(int height,int active,int love,int left,int right,int root)
{
insert2(root,active,love,0,1000,1);
///原来我把这句写在了left==right ,后来发现第 条答案不对,才意识到这句应该在外边。
if(left == right)
{
return;
}
int mid = (left+right)>>1;
if(height<=mid) insert1(height,active,love,lchild);
else insert1(height,active,love,rchild);
}
int query2(int row,int active1,int active2,int left,int right,int root)
{
///当前节点区间是要查询范围的 区间,返回节点值
if(active1<=left && right<=active2)
{
return a[row][root];
}
int mid = (left+right)>>1;
int ans = -1;
///递归查找 区间。
if(active1 <= mid) ans = query2(row,active1,active2,lchild);
if(active2 > mid) ans = max(ans,query2(row,active1,active2,rchild));
return ans;
}
int query1(int height1,int height2,int active1,int active2,int left,int right,int root)
{
if(height1<=left && right<=height2)
{
return query2(root,active1,active2,0,1000,1);
}
int mid = (left + right)>>1;
int ans = -1;
if(height1 <= mid) ans = query1(height1,height2,active1,active2,lchild);
if(height2 > mid) ans = max(ans,query1(height1,height2,active1,active2,rchild));
return ans;
}
int main()
{
int M;
while(~scanf("%d",&M))
{
if(M == 0) break;
char ch;
///直接将数组刷成-1.
memset(a,-1,sizeof(a));
for(int i = 1; i <= M; i++)
{
scanf(" %c",&ch);
if(ch == 'I') ///如果是I,插 条记录
{
int height;
double Active;
double Love;
scanf("%d%lf%lf",&height,&Active,&Love);
int A = (int)(Active*10); ///把活跃度放 倍,题 说了题中 数都是 位 数
int L = (int)(Love*10); ///把L也放 倍,这 放不放 都 insert1(height,A,L,0,200,1);
}
else ///如果是Q,查询相关记录
{
int height1,height2,temp;
double active1,active2;
scanf("%d%d%lf%lf",&height1,&height2,&active1,&active2);
int A1 = (int)(active1*10);
int A2 = (int)(active2*10);
///题 的 坑,输 的数据不 定从 到 。
if(height1 > height2)
{
temp = height1;
height1 = height2;
height2 = temp;
}
if(A1 > A2)
{
temp = A1;
A1 = A2;
A2 = temp;
}
int ans = query1(height1,height2,A1,A2,0,200,1);
if(ans == -1)
printf("-1\n");
else
printf("%.1lf\n",ans*0.1);
}
}
}
return 0;
}
七、扫描线
扫描线概念不好定义,就是向打印机扫描文件一样,有一条线,可以对界面进行扫描操作,扫描线是线段树这种数据结构的一种重要应用,可以用来求矩形面积并/周长等操作。在此介绍用线段树求矩形面积并和矩形周长。
1.线段树求矩形面积并
给出N个矩形的左下角坐标和右上角坐标,这N个矩形都是水平竖直这样摆放的,让求N个矩形面积的并。
其求解的基本思路是,将矩形的竖直的边按照横坐标从小到大排序,然后按顺序依次取这些边进行扫描。
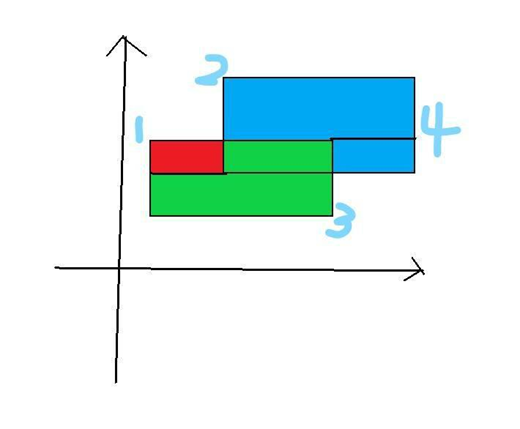
像图中所示,直线1向左扫描面积为0,直线2向左扫描面积为红色区域,直线3向左扫描面积为绿色区域,直线4向左扫描面积为蓝色区域。直观上很容易看明白,要将这个思路转化成代码,首先我们希望矩形的竖直的边按照横坐标从小到大的规则从自己的位置向左扫描,这个还是比较容易实现的,我们只需要存储竖直的线段,然后让他们按照从小到大排序就可以了。为了求得上面矩形的面积,我们需要保存每条竖直边端点的纵坐标,然后排序,以纵坐标的大小排序后,我们根据这个纵坐标的数组来构建线段树。
则我们把上图的矩形转化成下图:
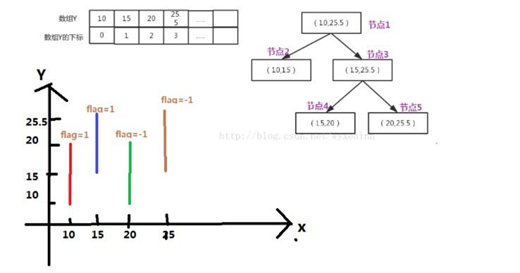
可以发现叶子节点所代表的区间实际是被矩形的纵边投影在纵轴之后,被切成的一段段区间,由于矩形左边和右边守恒,所以纵向的区域被多少条矩形左边界覆盖,就被多少条右边界覆盖。当向线段树中插入一条线段,线段在逐层递归后到达叶子节点,如果该叶子节点已被其它线段覆盖过,则当前线段与之前到达该区域的线段构成一个矩形的区域,统计该区域,如果到达该区域的线是矩形左边界,则该纵区域被覆盖次数加1,否则该纵区域被覆盖次数减一。并且每插入一条线段后,我们把该区域的横坐标留到其所到达的叶子节点,防止面积重复计算。
例题:HDU 1542:Atlantis
代码:
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <algorithm>
const int MAXN = 110;
using namespace std;
int n;
double Y[2*MAXN];
struct Line
{
double x; ///横坐标的值
double y1,y2; ///纵坐标的区间
int flag; ///flag等于1时,代表它是 形左边,flag等于-1时,代表它是 形右边
} line[2*MAXN];
struct NODE ///线段树节点类型
{
///最新到过该节点的线对应的x(横坐标的值)
double x;
double left,right; ///左边界,右边界
bool sign; /// 来标记该节点是否叶 节点
int cover; ///覆盖值
} node[MAXN<<3];
///这 不能使MAXN左移两位,因为有N个矩形,对应2*N个线段,则应该是2*N左移2位。
bool cmp(struct Line L1,struct Line L2)
{
return L1.x < L2.x;
}
void Build(int rt,int l,int r) ///l,r是Y数组的下标
{
node[rt].left = Y[l];
node[rt].right = Y[r];
node[rt].x = -1;
node[rt].sign = false; ///flase说明这个节点不是叶 节点
node[rt].cover = 0;
if(l+1 == r)
{
///叶 节点
node[rt].sign = true;
return;
}
int mid = (l+r)>>1;
Build(rt<<1,l,mid); ///递归构建左 树
Build(rt<<1|1,mid,r); ///递归构建右 树
}
///参数含义,rt为节点,line_x代表当前线对应的横坐标,l下界,r上界
///flag代表当前的线是 形的左侧的边还是右侧的边
double Calculate(int rt,double line_x,double l,double r,int flag)
{
if(r<=node[rt].left || l>=node[rt].right)
return 0;
if(node[rt].sign) ///代表其是叶 节点
{
if(node[rt].cover>0)
{
double pre = node[rt].x;
double ans = (line_x-pre)*(node[rt].right-node[rt].left);
node[rt].x = line_x;
node[rt].cover += flag;
return ans;
}
else
{
node[rt].x = line_x;
node[rt].cover += flag;
return 0;
}
}
double ans1 = Calculate(rt<<1,line_x,l,r,flag);
double ans2 = Calculate(rt<<1|1,line_x,l,r,flag);
return ans1+ans2;
}
int main()
{
int Case = 0;
double x1,y1,x2,y2;
while(~scanf("%d",&n))
{
if(n == 0)
break;
int i,j;
j = 0;
for(i = 0; i < n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
Y[j] = y1;
line[j].x = x1; /// 形左侧的边
line[j].y1 = y1;
line[j].y2 = y2;
line[j].flag = 1;
j++;
Y[j] = y2; /// 发型右侧的边
line[j].x = x2;
line[j].y1 = y1;
line[j].y2 = y2;
line[j].flag = -1;
j++;
}
sort(Y,Y+j); ///对纵坐标进 从 到 排序。
sort(line,line+j,cmp); ///对线的横坐标进 从 到 排序
Build(1,0,j-1); ///构建线段树
double union_area = 0;
for(i = 0; i < j; i++)
{
union_area += Calculate(1,line[i].x,line[i].y1,line[i].y2,line[i].flag);
}
printf("Test case #%d\n",++Case);
printf("Total explored area: %.2lf\n\n",union_area);
}
return 0;
}
1.线段树求矩形周长的并
给出N个矩形,拜访方式为水平竖直摆放,让求这N个矩形周长的并。
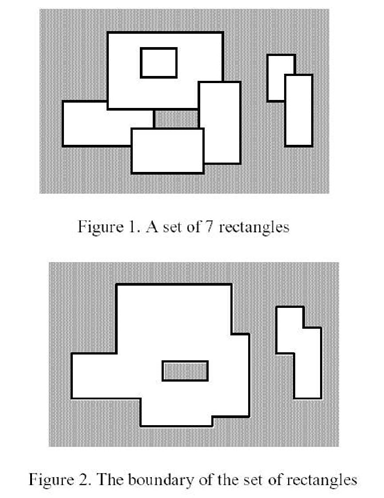
图一的N个矩形,矩形求并以后变成图二的图形,求图2图形周长的大小。这种问题有两种求法:(在此只介绍一种,另一种留做自学)
1.把图中的边分为横线、竖线去处理,对于横线即水平的边,我们按照其所在位置的纵坐标进行排序,然后从下到上插入线段,线段树区间维护的是该区间被线段覆盖的长度,每插入一个线段求一次总区间被覆盖的长度,然后减去上次总区间被覆盖的长度得到结果,该结果的绝对值就是新增加的周长,为什么是绝对值,因为对于一个矩形既有上边,也有下边,当上下边平衡的时候,这时候总区间的覆盖长度可能减少。然后水平线用线段树求解一次,竖直线用线段树求解一次,两次答案相加即为最后结果。
例题:HDU 1828:Picture
给出N个矩形,给出N个矩形的左下角坐标和右上角坐标,求N个矩形周长的并。
代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 5010;
const int maxm = 20010;
struct HLine
{
int y; ///横线对应的纵坐标
int x1,x2; ///横线对应的左右端点的横坐标
int flag; /// 来标记横线是矩形的上横线还是下横线
} hline[maxn<<3];
///竖直线
struct VLine
{
int x; ///竖线对应的横坐标
int y1,y2; ///竖线对应上下端点的纵坐标
int flag; /// 来标记该线是矩形的左边界还是右边界
} vline[maxn<<3];
bool cmp1(struct HLine L1,struct HLine L2)
{
return L1.y < L2.y;
}
bool cmp2(struct VLine L1,struct VLine L2)
{
return L1.x < L2.x;
}
struct Node
{
int left;
int right;
int cover;
int len;
} node[maxm<<2];
void build(int left,int right,int root)
{
node[root].left = left;
node[root].right = right;
node[root].cover = 0;
node[root].len = 0;
if(left == right)
{
return;
}
int mid = (left+right)>>1;
build(left,mid,root<<1);
build(mid+1,right,root<<1|1);
}
void update(int L,int R,int root,int flag)
{
if(L==node[root].left && R==node[root].right)
{
node[root].cover += flag;
if(node[root].cover)
{
node[root].len = node[root].right-node[root].left+1;
}
else if(node[root].left == node[root].right)
{
node[root].len = 0;
}
else
{
node[root].len = node[root<<1].len + node[root<<1|1].len;
}
return;
}
int mid = (node[root].left+node[root].right)>>1;
if(R <= mid) update(L,R,root<<1,flag);
else if(L>mid) update(L,R,root<<1|1,flag);
else
{
update(L,mid,root<<1,flag);
update(mid+1,R,root<<1|1,flag);
}
if(node[root].cover)
{
node[root].len = node[root].right-node[root].left+1;
}
else if(node[root].left == node[root].right)
{
node[root].len = 0;
}
else
{
node[root].len = node[root<<1].len + node[root<<1|1].len;
}
}
int main()
{
int N,x1,y1,x2,y2,cnt; ///cnt是线段条数,N个矩形,有2*N条线段
int minx,maxx,miny,maxy;
while(~scanf("%d",&N))
{
cnt = 0;
minx = miny = inf;
maxx = maxy = -inf;
for(int i = 1; i <= N; i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
minx = min(minx,x1);
maxx = max(maxx,x2);
miny = min(miny,y1);
maxy = max(maxy,y2);
///保存下横线信息
hline[cnt].y = y1;
hline[cnt].x1 = x1;
hline[cnt].x2 = x2;
hline[cnt].flag = 1;
///保存左竖线信息
vline[cnt].x = x1;
vline[cnt].y1 = y1;
vline[cnt].y2 = y2;
vline[cnt++].flag = 1;
///保存上横线信息
hline[cnt].y = y2;
hline[cnt].x1 = x1;
hline[cnt].x2 = x2;
hline[cnt].flag = -1;
///保存右横线信息
vline[cnt].x = x2;
vline[cnt].y1 = y1;
vline[cnt].y2 = y2;
vline[cnt++].flag = -1;
}
sort(hline,hline+cnt,cmp1);
sort(vline,vline+cnt,cmp2);
///处理 平线
build(minx,maxx,1);
int preCoverLen = 0;
int ans = 0;
for(int i = 0; i < cnt; i++)
{
update(hline[i].x1,hline[i].x2-1,1,hline[i].flag);
ans += abs(node[1].len-preCoverLen);
preCoverLen = node[1].len;
}
///处理竖直线
build(miny,maxy,1);
preCoverLen = 0;
for(int i = 0; i < cnt; i++)
{
update(vline[i].y1,vline[i].y2-1,1,vline[i].flag);
ans += abs(node[1].len - preCoverLen);
preCoverLen = node[1].len;
}
printf("%d\n",ans);
}
return 0;
}
八、题目推荐
1.单点更新
hdu 1166:敌兵布阵
hdu 1754: I Hate It
hdu 1394: Minimum Inversion Number hdu 2795:BillBoard poj 2828:Buy Tickets
poj 2886:Who Get the Most Candies?
hdu 4288: Coder
CodeforceBeta Round #19D:Points
poj 2481: Cows
hdu 3950: Parking log
hdu 4521: 小明系列问题-小明序列
CodeforceBeta Round #99(Div.1) C:Mushroom Gnomes
hdu 4605:Magic Ball Game
URAL 1989:Subpalindromes
hdu 4777: Rabbit Kingdom
2.区间更新
hdu 1698: Just a Hook
poj 3468: A SimpleProblem with Integers
poj 2528: Mayor' sposter
poj 1436: Horizeontally Visible Segments
poj 2991: Crane
CodeforceRound #136(Div.2) D:Little Elephant and Array uva 12436:RipVan Winkle's Code
codeforceRound #169(Div.2)E:Little Girl and Problemon Trees codeforceRound #35(Div.2)E:Parade zoj 3299:Fall the Brick
fzu 2105:Digits Count
hdu 4533:威威猫系列故事-晒被子
ural 1855:Trade Guilds of Erathia
hdu 4578:Transformation
hdu 4455:Substrings
hdu 4614: Vases and Flowers
hdu 4747: Mex
zoj 3724: Delivery
Codeforce 343D:Water Tree
ural 1977:Energy Wall
3.区间合并
poj 3667: Hotel
hdu 3308: LCIS
hdu 3397: Sequence operation
hdu 2871: Memory Control
hdu 1450: Tunnel Warfare CodeforceBeta Round #43 D:Parking lot
4.扫描线
hdu 1542: Atlantis
hdu 1828: Picture
hdu 1255: 覆盖的面积
hdu 3642: Get the Treasury
poj 2482: Stars in Your Window
poj 2464: BrowniePoints II
hdu 3255: Farming
uva 11983: WeirdAdvertisement
hdu 4052: Adding New Machine
hdu 4419: Colorful Rectangle
zoj 3521: Fairy Wars
zoj 3525: Disppearance
5.一堆线段树的题目
poj 2104:Kth-Number
hdu 1832:Luck and Love

 浙公网安备 33010602011771号
浙公网安备 33010602011771号