在我们考虑到要对一个区间进行操作的时候,第一解法就是想到运用暴力大法,但是难免会面临着超时的危险。有没有一种方法可以很好的解决这种区间操作呢?
首先先考虑一下这三个问题:
问题一:
(1)有一个机器,支持两种操作,在区间[1,10000]上进行。
操作A:把位置x的值+k
操作B:询问区间[l,r]所有数字之和
区间的初始值全部为0
现在你要充当这个机器,操作A和操作B会被穿插着安排给你,要求对于所有操作B,给出正确的答案。
怎样做才能最节省精力?
问题二:
(2)有一个机器,支持两种操作,在区间[1,10000]上进行。
操作A:把区间[l,r]的值全都+x
操作B:询问位置x的值。
区间的初始值全部为0
现在你要充当这个机器,操作A和操作B会被穿插着安排给你,要求对于所有操作B,给出正确的答案。
怎样做才能最节省精力?
问题三:
(3)有一个机器,支持两种操作,在区间[1,10000]上进行。
操作A:把区间[l,r]的值全都+x
操作B:询问区间[l,r]所有数字之和
区间的初始值全部为0
现在你要充当这个机器,操作A和操作B会被穿插着安排给你,要求对于所有操作B,给出正确的答案。
怎样做才能最节省精力?
三个问题中操作的数量都可以认为是10000(甚至有可能会更大)
注意:
1.举个例子,进行这种类似的操作:
从一行任意打乱的数字中找一个数字
不能认为一瞬间就可以找到,在这里所花费的精力和数字的总数具有线性关系。
2.我们认为将数据转换为二进制不需要任何时间。
对于问题1,如果我们每种操作都暴力进行,那么显然总的时间复杂度为O(mA+n*mB),n表示区间长度,mA表示操作A执行的次数,mB表示操作B执行的次数。
那么有没有一种更加轻松的办法呢?
我们将引入一种数据结构,叫做<树状数组>。
首先了解一下在整个树状数组知识中起到非常重要的作用的一个东西,可所谓是树状数组的核心,应用的却说很巧妙。
lowbit(x)=x&((~x)+1) (为了少引入补码的概念,我们这里稍微麻烦了一下,其实x&-x就行)
它的作用是什么呢?
它只保留“从低位向高位数,第一个数字1”作为运算结果
比如二进制数00011100,执行这个函数后,结果就是00000100,也就是4。
二进制数11111001,执行这个函数后,结果就是00000001,也就是1
那么这种运算对我们的算法有什么帮助呢?
首先我们来解决一下问题1。
先列举出从1~32的lowbit,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32
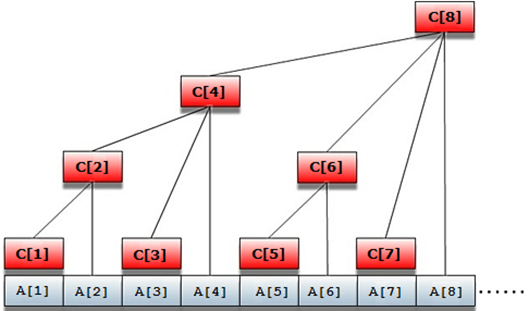
我们让第i个位置管理[i-lowbit(i)+1,i]这一段区间,示意图如下:
怎么看每个数字管理多少?
就是从自己本身开始往前数,连续数i+lowbit(i)个位置的数。

定义:a []= [ 1, 2, 3, 4, 5, 6, 7, 8];
用c数组来管理a数组
c[1] = a[1];
c[2] = a[1] + a[2];
c[3] = a[3];
c[4] = a[1] + a[2] + a[3] + a[4];
c[5] = a[5];
c[6] = a[5] + a[6];
c[7] = a[7];
c[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8];
此时c数组就是这个树状数组了,c[x]保存的是从下标x开始 a[x]+a[x-1]+a[x-2]+a[x-k] ,至于有几个a[]相加,这里有一个计算方法,把x化为二进制,从右向左找到第一个1的位置,这个位置所代表的十进制的数字k就意味着c[x]=a[x]+a[x-1]+a[x-2]+...+a[x-k-1];
假如x=6 把6化为二进制:110 ,从右向左找到第一个1的位置 就是 10 ,十进制就是2,那么 c[6]=a[6]+a[5];
假如x=8 的二进制是1000 ,从右向左找到第一个1的位置 就是 1000,十进制就是8 ,那么c[8]=a[8]+a[7]+a[6]+a[5]+a[4]+a[3]+a[2]+a[1];
我们每次执行操作A(把位置x的值+k),只需要把“能管理到x的所有位置”都+k就行,最终的效果如图所示:
那么怎样快速找到哪些位置能管理到x呢?
答案还是lowbit
我们先更新x,然后把x赋给一个新值,x+lowbit(x),那么新值依然可以管理到x,这样依次类推直到x>10000即可。
比如x=2,那么首先把2的值+k,这不用说。
然后x的新值=x+lowbit(x)=2+lowbit(2)=4,对着上面的示意图看看,会发现4确实能管理到2,那么把4的位置+k
然后再来一遍,x=4+lowbit(4)=8,发现8还是能管理到2,继续给8这个位置+k,就这样依次类推下去直到x=16384时,超过10000了,操作完成。
这样操作之后,树状数组里每一位当前存的值可能并不是该位置的实际值,为了方便区分,在下文中我们把实际值叫做"原数组的值",当前值就叫做"树状数组的值"。
可以证明,对于任意一个x属于[1,10000]我们最多进行log(2,10000)次操作,就可以完成操作A
那么把操作A变复杂(从O(1)变到O(logn))能换来什么好处?
答案就是,可以把操作B的时间复杂度降低成log级别的。
询问区间[L,R]的和sum(L,R)。我们只需要求出sum(1,R)和sum(1,L-1),然后sum(1,R)-sum(1,L-1)就是sum(L,R)了。
那么对于任意的x,sum(1,x)怎么求呢?
我们把最终得到的答案存在ans变量中,执行下面的操作:
(1)ans初始化为0
(2)ans加上x位置的值
(3)给x赋予新值 x-lowbit(x)
(4)如果x>0则跳回操作(2),否则结束算法。
举个例子介绍一下:
一开始我们还是停留在树状数组第x位置上(比如x=6吧),答案一开始为0。
还记得吗,我们在进行“给原数组第x位置的数增加k”这个操作时,把“能管理到x的所有位置”都增加了k。
那么,对于任意一个位置,树状数组里的值就是"它能管理到的所有位置上,原数组的值之和"。
因此我们给答案加上树状数组第x位置的值,这里就得到了sum(5,6),因为6能管理[5,6],然后给x减去lowbit(x),得到4。再加上x位置的值,也就是sum(1,4),因为4能管理[1,4],再让x=x-lowbit(x),得到0,由于不再大于0,算法终止,得到答案,这时答案恰好是sum(1,6)。
依然可以证明,最多只需要进行log级别次数的查询,这样我们进行操作B的时间复杂度也是log级别了。
lowbit(int x)函数可写成
int lowbit(int x)
{
return x&(-x);
}
建立树状数组
void Build(int n)
{
for (int i=1; i<=n; i++)
for (int j=i; j>=i-lowbit(i)+1; j--)
c[i]+=a[j];
}
更新树状数组
void update(int id,int value)
{
for (int i=id; i<=MAX; i+=lowbit(i))//i+=lowbit(i)得到的是i的父节点
c[i]+=value;
}
求和(从1到n的和)
int sum(int n)
{
int ans=0;
for (int i=n; i>0; i-=lowbit(i))//i-=lowbit(i) 得到是i的子节点
ans+=c[i];
return ans;
}
问题二(树状数组区间修改+单点查询)
用差分的方法,区间[l,r]所有值+k改成"位置l加上k,位置r+1减去k"
查询的时候直接查询sum(1,x)就行
问题三(树状数组区间修改+区间查询)
设原数组第i位的值为ai,di=ai−a[i−1],则有(这里认为a0=0):

所以有:
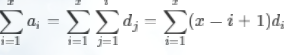
于是我们得到了:
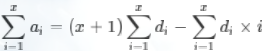
于是我们把原数组差分后维护两个树状数组,一个维护di,一个维护di×i。
这样区间求和时可以在两个树状数组中查询得到前缀和,区间修改时就是差分数组的修改,每次修改两个点即可。
其中c1i维护的是d[i],c2[i]维护的是d[i]×i。
核心代码:
void update(int x,int val)
{
for(int i=x; i<=n; i+=lowbit(i))
{
c1[i]+=val;
c2[i]+=(long long)x*val; //给差分数组中的位置x加上y
}
}
long long sum(int x) //查询前x项的和
{
long long ans=0;
for(int i=x; i; i-=lowbit(i))
ans+=(x+1)*c1[i]-c2[i];
return ans;
}
二、树状数组可以扩充到二维。
问题:一个由数字构成的大矩阵,能进行两种操作
-
对矩阵里的某个数加上一个整数(可正可负)
-
查询某个子矩阵里所有数字的和,要求对每次查询,输出结果。
一维树状数组很容易扩展到二维,在二维情况下:数组A的树状数组定义为:
C[x][y] = ∑ a[i][j], 其中,
x-lowbit(x) + 1 <= i <= x,
y-lowbit(y) + 1 <= j <= y.
例:举个例子来看看C的组成。
设原始二维数组为:
A[][]={{a11,a12,a13,a14,a15,a16,a17,a18,a19},
{a21,a22,a23,a24,a25,a26,a27,a28,a29},
{a31,a32,a33,a34,a35,a36,a37,a38,a39},
{a41,a42,a43,a44,a45,a46,a47,a48,a49}};
那么它对应的二维树状数组C呢?
记:
B[1]={a11,a11+a12,a13,a11+a12+a13+a14,a15,a15+a16,...} 这是第一行的一维树状数组
B[2]={a21,a21+a22,a23,a21+a22+a23+a24,a25,a25+a26,...} 这是第二行的一维树状数组
B[3]={a31,a31+a32,a33,a31+a32+a33+a34,a35,a35+a36,...} 这是第三行的一维树状数组
B[4]={a41,a41+a42,a43,a41+a42+a43+a44,a45,a45+a46,...} 这是第四行的一维树状数组
那么:
C[1][1]=a11,C[1][2]=a11+a12,C[1][3]=a13,C[1][4]=a11+a12+a13+a14,
c[1][5]=a15,C[1][6]=a15+a16,...
这是A第一行的一维树状数组
C[2][1]=a11+a21,C[2][2]=a11+a12+a21+a22,C[2][3]=a13+a23,
C[2][4]=a11+a12+a13+a14+a21+a22+a23+a24, C[2][5]=a15+a25,
C[2][6]=a15+a16+a25+a26,...
这是A数组第一行与第二行相加后的树状数组
C[3][1]=a31,C[3][2]=a31+a32,C[3][3]=a33,C[3][4]=a31+a32+a33+a34,
C[3][5]=a35,C[3][6]=a35+a36,...
这是A第三行的一维树状数组
C[4][1]=a11+a21+a31+a41,C[4][2]=a11+a12+a21+a22+a31+a32+a41+a42,
C[4][3]=a13+a23+a33+a43,...
这是A数组第一行+第二行+第三行+第四行后的树状数组
搞清楚了二维树状数组C的规律了吗? 仔细研究一下,会发现:
(1)在二维情况下,如果修改了Ai=delta,则对应的二维树状数组更新函数为:
void add(int x,int y,int d)
{
int i,j;
for(i = x; i<=n; i+=lowbit(i))
for(j = y; j<=n; j+=lowbit(j))
c[i][j]+=d;
}
(2)在二维情况下,求子矩阵元素之和∑ a[i]j的函数为
int sum(int x,int y)
{
int ret=0,i,j;
for(i = x; i>0; i-=lowbit(i))
for(j = y; j>0; j-=lowbit(j))
ret+=c[i][j];
return ret;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号