二叉搜索树是一种很实用的数据结构,二叉搜索树上所有的节点,都满足左子数上所有的节点都比自己的小,而右子数上所有的节点都比自己大这一条件。
下图就是一个二叉搜索树的例子:

二叉搜索树的查询
例如:在上图的二叉搜索树中查询书否存在10
1.根节点的数值是7,比10小,所以往右儿子节点走。
2.走到的节点数值是15,比10大,所以往左儿子节点走。
3.走到的节点是10,因此10在集合中。

二叉搜索树的插入
如果我们按照查找数值的方法试图查找这个数值的节点,就可以知道其对应节点的所在位置,之后再那个位置插入节点即可。例如,插入数值6。和查找的方法类似,从根节点出发,通过“左-->右”两步,就可以知道6应该是5的右孩子,因此在5的右孩子的位置插入6的节点即可。

二叉搜索树的删除
例如:我们要删除数值15。如果删除了15所在的节点,那么它的两个儿子10和17就悬空了。于是,把11提到15所在的位置就可以解决问题。
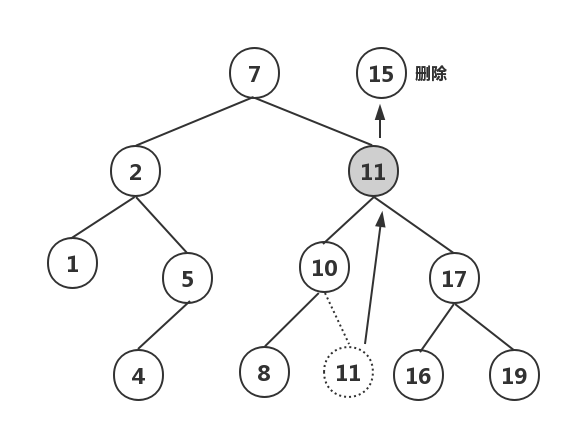
一般来说,删除的时候应该根据以下几种情况进行处理:
1.需要删除的节点没有左孩子,那么就把右孩子提上去。
2.需要删除的节点的左孩子没有右孩子,那么就把左孩子提上去。
3.以上两种情况都不满足的话,就把左孩子的子孙中最大的节点提到需要删除的节点上。
///表示节点的结构体
struct Node
{
int val;
Node *lch,*rch;
};
///插入节点x
Node *insert(Node *p,int x)
{
if(p==NULL)
{
Node *p=new Node;
p->val=x;
p->lch=p->rch=NULL;
return p;
}
else
{
if(x<p->val)
p->lch=insert(p->lch,x);
else
p->rch=insert(p->rch,x);
return p;
}
}
///查找节点x
bool find(Node *p,int x)
{
if(p==NULL)
return false;
else if(x==p->val )
return true;
else if(x<p->val )
return find(p->lch,x);
else
return find(p->rch,x);
}
///删除节点x
Node *remove(Node *p,int x)
{
if(p==NULL) return NULL;
else if(x<p->val ) p->lch=remove(p->lch,x);
else if(x>p->val ) p->rch=remove(p->rch,x);
else if(p->lch==NULL)
{
Node *q=p->rch;
delete p;
return q;
}
else if(p->lch->rch==NULL)
{
Node *q=p->lch;
q->rch=p->rch;
delete p;
return q;
}
else
{
Node *q;
for(q=p->lch;q->rch->rch!=NULL;q=q->rch);
Node *r=q->rch;
q->rch=r->lch;
r->lch=p->lch;
r->rch=p->rch;
delete p;
return r;
}
return p;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号