从刚体动力学方程到 MATLAB 多种方法仿真验证
终于结束了自己的毕设设计,这半年的时间一直在和刚体动力学仿真硬磕,关于这方面的网络资源不太多,因此在这里将自己不断摸索学到的方法做一个概括阐述,希望能够为同样饱受困扰的读者提供一些帮助。
程序开源地址:刚体动力学仿真示例程序
〇、问题阐述
一般情况下,刚体系统具备这样形式的动力学方程:
其中,\(q\) 为系统广义坐标,\(D(q)\) 为惯性矩阵,\(C(q,\dot{q})\) 为离心力及科里奥利力项,\(G(q)\) 为重力项,\(U\) 为广义力项。
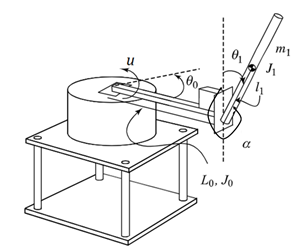
为方便阐述,这里以 一阶旋转倒立摆 这一简单多刚体系统为研究对象,探讨该系统的动力学仿真问题。参考文献[1],在不考虑系统摩擦等不确定因素干扰情况下,给出各项具体形式为:
其中,广义坐标 \(q = [\theta_0,\theta_1]^T\),\(J_0\) 为旋臂绕电机转轴的转动惯量,\(L_0\) 为旋臂总长,\(m_1\) 为摆杆质量,\(l_1\) 为摆臂从其质心到与旋臂转动关节间的长度,\(J_1\) 为摆杆绕其质心的转动惯量,\(\theta_0\) 为旋臂转动角度,\(\theta_1\) 为摆杆作顺时针运动时与垂直线间的夹角大小,\(\tau\) 为输入力矩。
本质上该系统的这一仿真问题就是其动力学方程(常微分方程)的求解问题。借由 MATLAB 可以有如下几种解决思路:
- (1)ODE 求解器
- 纯文本编程,方便快速开发,十分适用于与其他算法(参数寻优、复杂控制算法)结合使用;
- 在一些奇异点会出现难以求解的情况,诸如一阶旋转倒立摆系统在直立位置 \([\theta_0,\theta_1]^T = [0°,0°]^T\);
- 未找到支持求解过程进行中断的功能,因此针对以系统状态变量作派生的函数诸如系统能量、李雅普诺夫函数等,需要在求解过程完全结束后二次计算,不够优美;
- (2)Simulink 初级使用 —— 基础模块
- 利用 Simulink 中诸如矩阵单元、微积分单元、加减乘除单元等基础单元进行动力学方程的表述
- 工程量很大,不符合快速开发这一重要前提
- (3)Simulink 进阶使用 —— S-function 模块
- 文本编程与图形化编程结合,功能实现支持 m语言、C语言等常见编程语言,以模块形式在 Simulink 中被调用;
- 灵活度不够高,基本上是按照固定模板进行程序编写,对于一些内部参数(诸如物理参数、系统能量等)没办法直接传递到模块外(只能传递选定的系统状态变量);
- 当结合硬件在环技术(例如 QUARC)时编译工作很麻烦;
- (4)Simulink 高阶使用 —— Simscape Multibody 工具箱
- 三维仿真,完成实体、关节及变换坐标系之后,系统能自行进行动力学求解,省去了动力学方程的直接表述工作;
- 基于物理模型的动力学建模,为与物理系统保持尽量一致的运动特性,往往需要精确的三维模型参数(长度、质量、惯性系数等);
- 没有碰撞箱
- 手动装配比较麻烦,特别是各个坐标系之间的转换很繁琐;安装相应插件后支持从SolidWorks 导出的装配体模型直接导入Simscape Multibody中,并自动生成相应的模型文件,但是生成算法不够智能,对于复杂模型会存在一些怪异的装配方式。
一、方法 ①:ODE 求解器
ODE 求解器实际是 MATLAB 提供的一系列常微分方程(Ordinary Differential Equation)的求解函数集合,根据不同求解场景,有 ode45、ode23、ode113等8种基本求解器(详见 选择 ODE 求解器 -- MathWorks 中国)。对于多刚体系统,一般选择以基于显式 Runge-Kutta (4,5) 公式的 ode45 求解器即可。该求解器的基本函数形式及各参数解释为:
[t,x] = ode45(odefun,tspan,x0,options),
odefun:待积分函数的句柄。亦即描述微分方程 \(\dot{x} = f(t,x)\) 的函数的句柄,函数基本形式为 dx = odefun(t,x),其中odefun亦即 \(f\);
tspan:积分区间。亦即待求解问题的总时间跨度;
y0:变量初始状态。亦即待求解状态变量的初始值;
options:一些额外的求解条件构成的结构体,包含求解精度、求解方法等。
对于一阶旋转倒立摆系统,可选取系统状态变量 \(x = [\theta_0,\dot{\theta}_0,\theta_1,\dot{\theta}_1]^T\),而 odefun要求返回值 \(\dot{x} =[\dot{\theta}_0,\ddot{\theta}_0,\dot{\theta}_1,\ddot{\theta}_1]^T\),必须借助系统动力学方程作为转换手段,亦即 \(\ddot{q}=[\ddot{\theta}_0,\ddot{\theta}_1]^T = D^{-1}(U-C·\dot{q}-G)\),因此整个求解流程可总结伪代码为:
function main:
① 定义初始条件(包含求解时长,系统初始状态,额外求解条件等)
② [t,x] = ode45(odefun,tspan,x0,options);
end
function dx = odefun(t,x):
① 物理参数初始化(质量、长度、惯性系数等)
② 各系数矩阵定义(D、C、G、U)
③ dq = [x(2);x(4)]
④ ddq = inv(D)*(U-C*dq-G) % 动力学方程
⑤ dx = [dq(1);ddq(1);dq(2);ddq(2)]
end
针对一阶旋转倒立摆系统在摆杆处于水平位置\([\theta_0,\dot{\theta}_0,\theta_1,\dot{\theta}_1]^T=[0°,0,90°,0]\)的零输入响应过程,仿照上述伪代码可撰写核心程序如下:
%% ode 初始化
T_stop=10;% 仿真时长 s
T_sample = 0.002;% 采样周期 s
x0 = [0;0;1/2*pi;0];% 初始状态 [q0;dq0;q1;dq1]; 期望状态 x_f = [0;0;0;0];
options=odeset('RelTol',1.0e-6,'AbsTol',1.0e-6,'BDF','on');%设置仿真精度,Backward Differentiation Formulas (BDFs) instead of the default Numerical Differentiation Formulas (NDFs).
%% ode 求解
[t,x]=ode45(@(t,x) RIP_Sysm(t,x),[0:T_sample:T_stop],x0,options); % ode45解常微分方程
%% 绘图
figure(1)
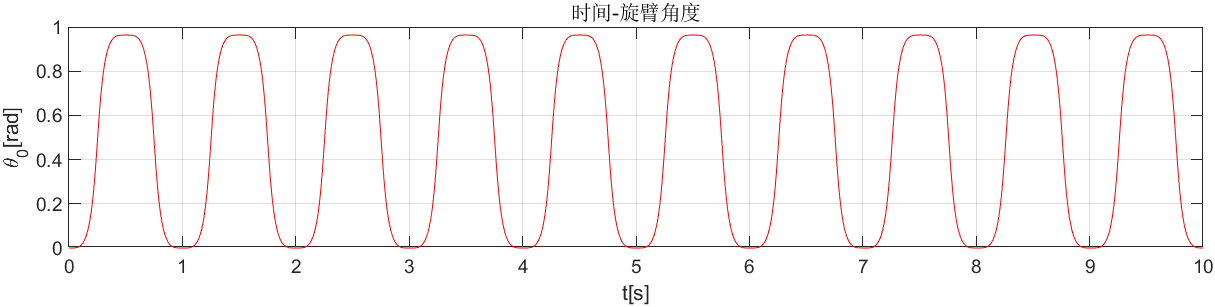
plot(t,x(:,1));title('时间-旋臂角度');
xlabel('t[s]');ylabel('\theta_0[rad]')
figure(2)
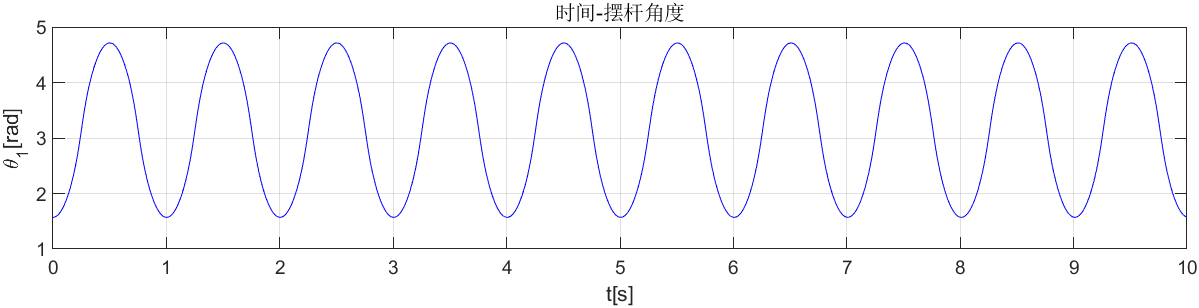
plot(t,x(:,3));title('时间-摆杆角度');
xlabel('t[s]');ylabel('\theta_1[rad]')
%% 待积分函数
function dx = RIP_Sysm(t,x)
%% Constants
L_0 = 0.2159; %Total lenth of the arm
l_1 = 0.1556; % Distance from pivot to center of pendulum's mass
m_1 = 0.1270; % Mass of pendulum
J_0 = 0.0020; % Inertia of the arm about the rotation axis
J_1 = 0.0012; % Pendulum moment of intertia about center of mass
g = 9.80; % Acc of the gravity
%% D(q) 正定惯性矩阵
D_11 = J_0 + m_1*(L_0^2+l_1^2*sin(x(3))^2);
D_12 = m_1*l_1*L_0*cos(x(3));
D_21 = D_12;
D_22 = J_1 + m_1*l_1^2;
D=[D_11,D_12;D_21,D_22];
D_inv =inv(D);
% C(q,dq) 离心力和哥氏力
C_11 = 1/2*m_1*l_1^2*sin(2*x(3))*x(4);
C_12 = -m_1*l_1*L_0*sin(x(3))*x(4)+1/2*m_1*l_1^2*sin(2*x(3))*x(2);
C_21 = -1/2*m_1*l_1^2*sin(2*x(3))*x(2);
C_22 = 0;
C = [C_11,C_12;C_21,C_22];
% G(q) 重力
G = [0; -m_1*g*l_1*sin(x(3))];
U = [0;0];%零输入响应
dq=[x(2);x(4)]; % 角度 x1的导数,x2的导数
ddq= D_inv*(U - C*dq - G ); % 动力学方程反解角加速度:D(q)*ddq + C*dq + G = U
dx = [dq(1);ddq(1);dq(2);ddq(2)];
end
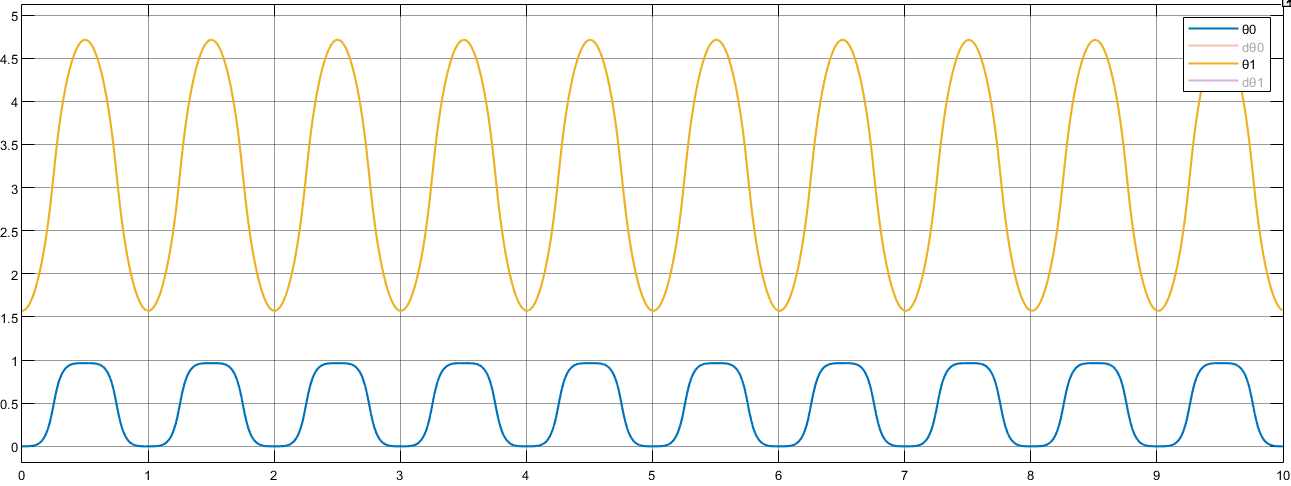
旋臂及摆杆运动曲线结果如下,由于未引入摩擦阻尼等因素,因此系统作近似正弦运动(不完全是,摆杆一部分势能转换为旋臂动能)。
 |
 |
二、方法 ②:Simulink 初级使用 —— 基础模块
三、方法 ③:Simulink 进阶使用 —— S-function 模块
S-Function 是 Simulink 中一个很好的连接图形化及文本编程的模块工具,它能够按仿真时间序列,依赖各项回调函数完成系统初始化、系统状态求导及系统状态输出等工作[2] ,整个过程由该模块自迭代完成。
具体说来,为满足描述刚体动力学方程的需求,S-Function 需要定义:
主入口函数:用于根据仿真时间序列进行 S-Function 的状态分流(类似于状态机)。形如 rip_plant(t,x,u,flag),其中 t 为仿真时间,x 为状态变量,u 为控制输入,flag 即为仿真环境自动提供的当前运行状态标志;
初始化函数:用于对被描述系统的各变量进行初始化表述,包含连续(离散)状态变量个数、输入量个数、输出量个数、采样方式(连续 or 离散)及周期(定周期 or 变周期)等;
状态求导函数:用于完成系统状态变量的求导工作,即执行 \(\ddot{q}=[\ddot{\theta}_0,\ddot{\theta}_1]^T = D^{-1}(U-C·\dot{q}-G)\) 算式;
输出函数:用于输出系统状态变量。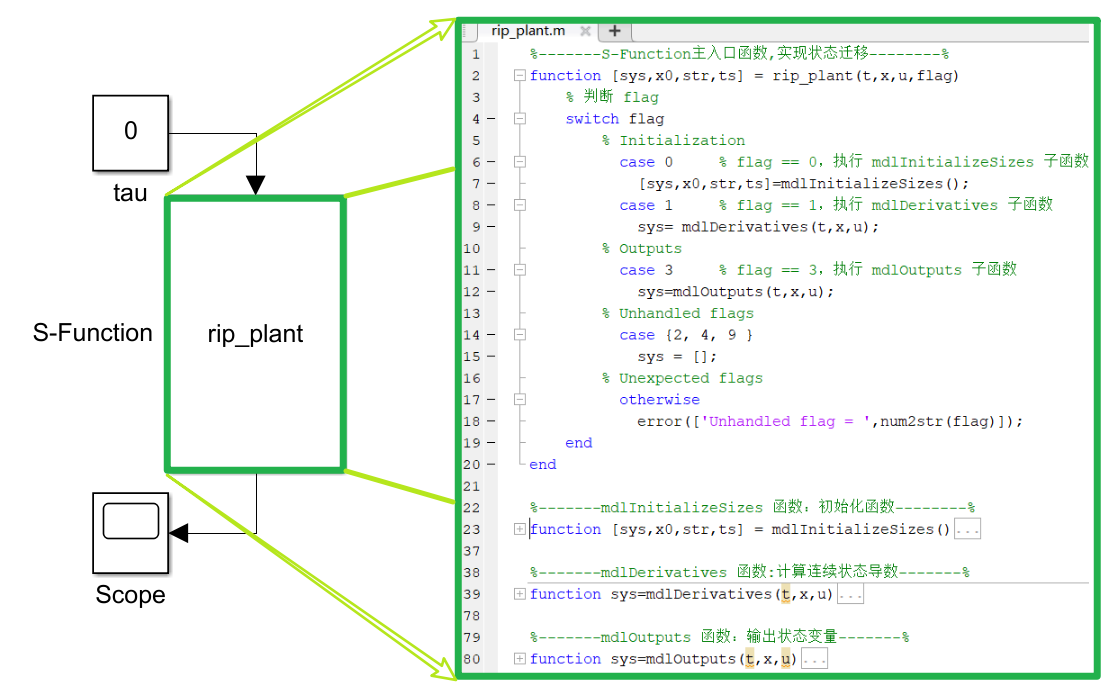
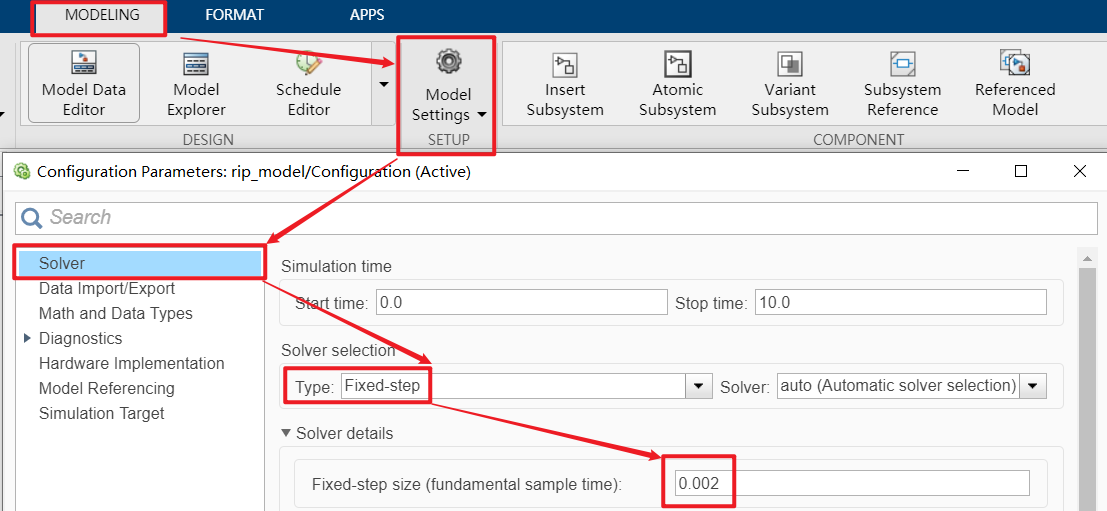
特别注意,针对一阶旋转倒立摆系统,为与 方法 ①:ODE 求解器 结果保持一致,需要设置求解器为定步长且补偿为 0.002s(变步长时,有时步长过大容易产生漂移)。
运行仿真模型,其结果与方法 ① 的结果一致:
四、方法 ④:Simulink 高阶使用 —— Simscape Multibody 工具箱
Simscape Multibody 提供了适用于诸如机器人、汽车悬架、建筑设备等的 3D 机械系统多体仿真环境。借助表示刚体、关节、约束、力元件和传感器的模块,可以实现对多体系统的三维建模。Simscape Multibody 会根据使用者所创建的机械模型自动建立起整个机械系统的运动方程并进行求解。对于一些复杂的机械系统,借助一些插件工具可将完整的 CAD 装配件(包括质量、惯性、关节、约束和 3D 几何结构)导入到仿真模型中·,极大地简化了复杂模型的装配工作。
- 工具箱直接在 MATLAB 视窗主页菜单栏的“附加功能”搜索安装即可

- 关于将 SolidWorks 的装配件直接导入到 Simscape Multibody 的方法可参考:
Matlab模型可视化仿真:SimMechanics Link的安装与使用-知乎-作者:llllq
对于一阶旋转倒立摆系统,由于整个系统机械结构比较简单,因此直接利用该工具箱中的 Solid 模块、Joint 模块以及 Tuansfiorm 模块等简单模块作手动装配即可表述其三维结构。
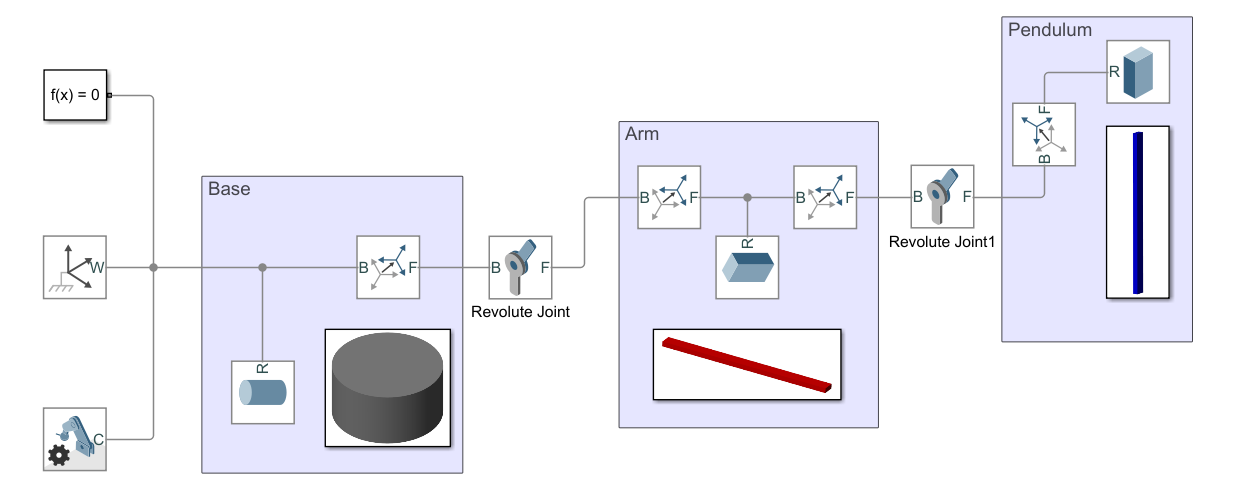
通过运行该仿真模型,可以在 MATLAB 的 Mechanics Explorer 视窗观察到系统作自由响应的三维动画,关节角度及角速度可由示波器 Scope 进行观察:
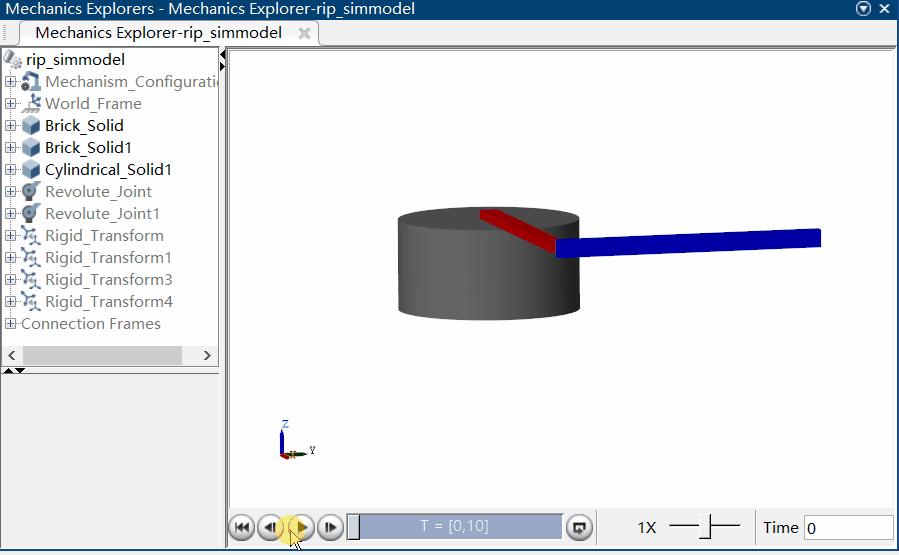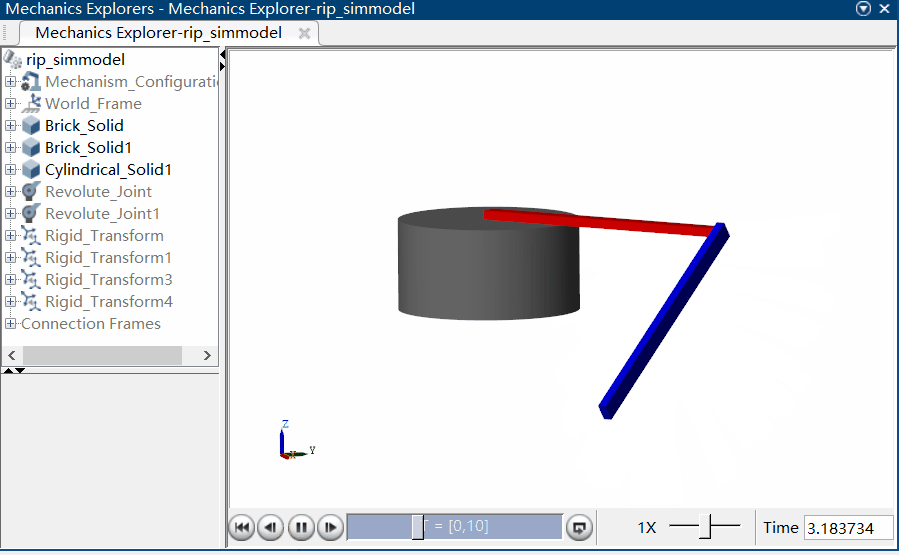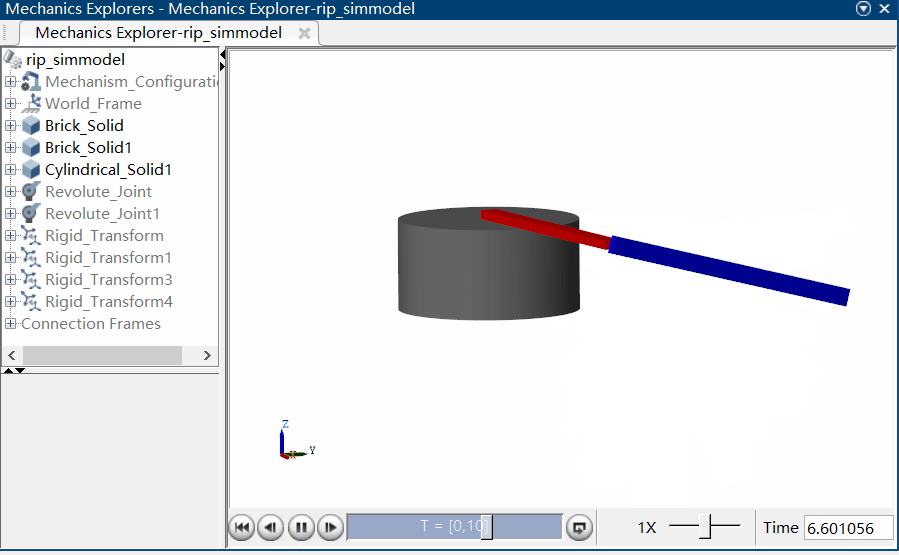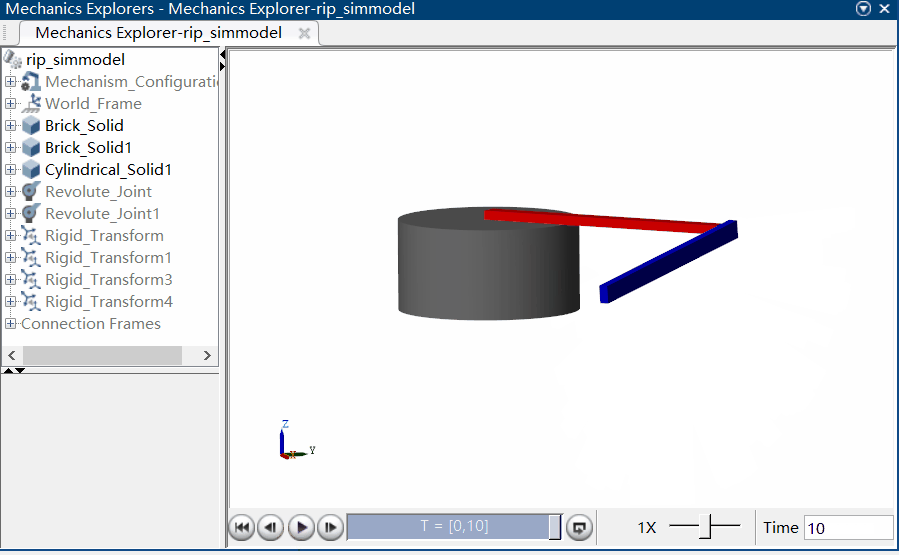 |
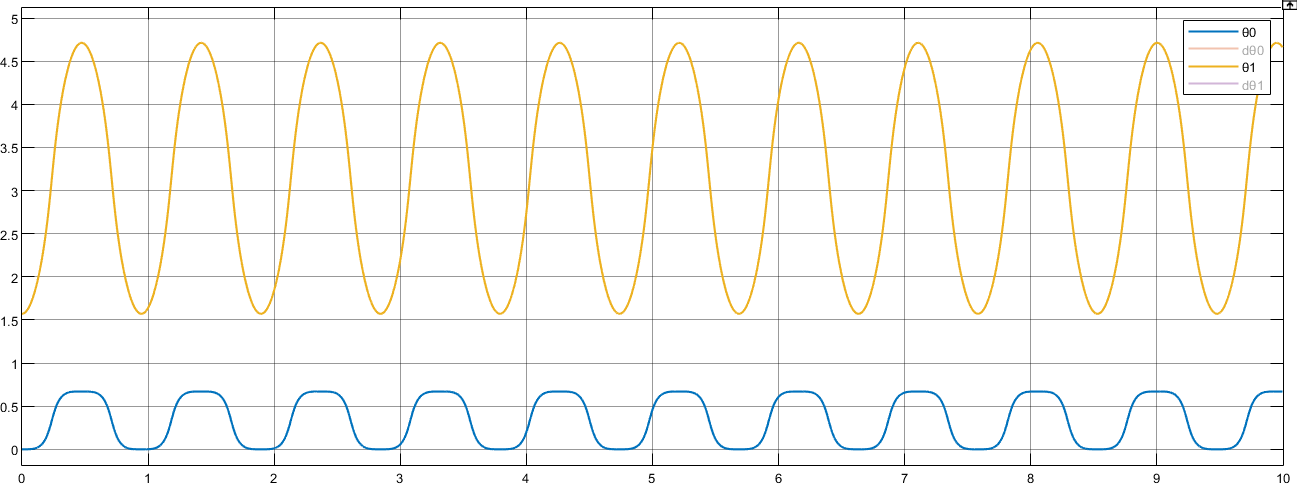 |
五、注意事项
- (1)关于 ode45 如何设置定步长问题(求解非刚性微分方程 - 中阶方法 - MathWorks)
- 答:一般来说 ode45 函数的变步长调用方式为
[t,x] = ode45(odefun,tspan = [0,Tf],x0,options),注意到此时tspan = [0,Ts],返回值[t,x]为变步长求解时刻及对应时刻的系统状态变量组成的集合;从原理上来说,ode45 本身求解过程是变步长这一事实不能更改,但是该函数提供了一种插值的方式以使得使用者可以获取到指定时刻的系统状态,此时该函数的调用方式为[t,x] = ode45(odefun,tspan = [0:Ts:Tf],x0,options),注意到此时tspan = [0:Ts:Tf],Ts即为采样周期。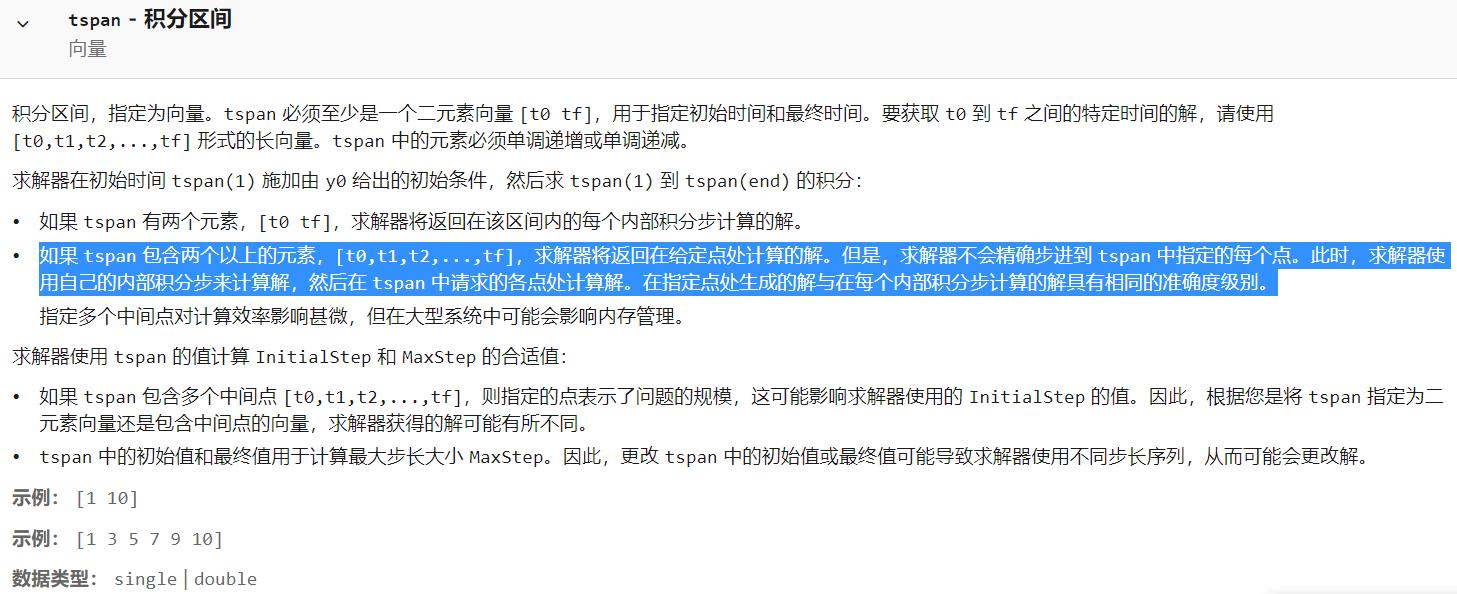
- (2)程序开源地址:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号