CVPR2019 Oral论文《Side Window Filtering》解读及算法 Python 实现
摘要
2019 年国际计算机视觉领域顶尖会议 CVPR 收纳了一篇来自国内学者殷慧、龚元浩及邱国平提出的一个新颖的图像滤波算法论文。文章提出了一种新型的侧窗滤波算法,解决了传统滤波算法会造成图像边缘模糊而丢失边缘信息的问题。文章名字很简短 -- 《Side Window Filtering》,甚至连算法的思想也不是很复杂,但是呈现的结果却十分优秀。在拜读这篇文章之后,决定对文章做二次的解剖分析和整理,并对文中提到的部分算法进行复现,作为本学期《数字图像处理》课程的结课报告。下面是在利用 Latex 进行排版前的 md 草稿,文章内容与最终报告提交 pdf 核心内容差不多,只是在措辞上进行了些许润色,故不再重新修改。
待解决的问题
在计算机图像处理领域,图像滤波这一基础算法被大量地使用,但是常见的滤波算法都是将滤波核的中心与待处理的像素位置对准,再对该像素的邻接像素做一定的运算操作。一类常见的线性逼近的图像滤波操作,比如均值滤波、盒子滤波核和高斯滤波等,是将某一次逼近结果近似为一个像素在其局部滤波窗口内的邻接像素的加权计算结果,即:
其中 \(\Omega _i\) 为局部滤波窗口内的像素,\(\omega _{ij}\) 是权重,\(q\) 为像素值,\(I_i\) 滤波计算结果。那么从上式中我们能够直观地知道影响计算结果的一个因素是滤波核函数的权重选择。但是在权重设置不变或者说是基本思想不变的情况下,另一个能够影响滤波结果的就是窗口本身的形状和尺寸的选择了。
假设现在我们有一个尺寸为 3x3 的单通道图像,规定1为白色,0为黑色,它具有明显的边缘,如 Fig.1 所示。我们选择滤波方式为均值滤波,滤波核大小为 3x3,现在我们来考虑处于正中心位置的像素的滤波结果,很明显以传统的均值滤波方式,我们可以得到下列结果,如 Fig.2 所示。

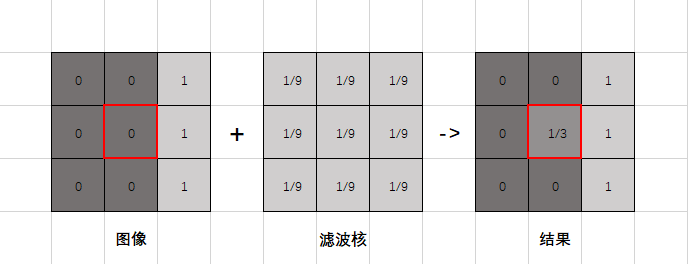
很明显,经过均值滤波之后,原本介于黑白交界处的中心像素的值被拉高到了 \(\frac{1}{3}\) ,与原本的像素值 \(0\) 相比,发生了较大的改变。
更一般地,我们有如下典型的理想边缘模型,分别是阶跃边缘、斜坡边缘和屋顶型边缘,如 Fig.3 所示
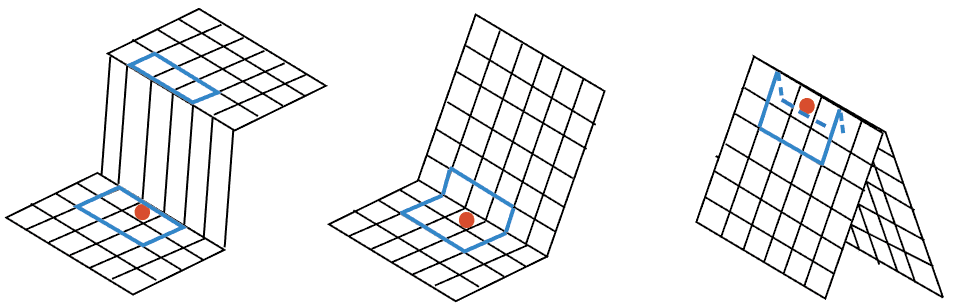
从宏观来看,若是对于一幅具有类似边缘的图像,经过传统滤波处理之后,其边缘必定在一定程度上被平滑,甚至导致边缘信息消失,而这往往是我们不期望得到的结果。因此,我们需要重新考虑窗口的样式设计。
算法思想
经过以上的分析,可以发现传统滤波算法出现边缘模糊这类现象的根本原因在于他们几乎都将待处理像素置于其核函数的中心位置,而这样会导致滤波窗口在跨越边缘时,引入对来自于边缘两侧像素值的加权计算。一旦经过这样的计算,将会导致边缘信息在沿边缘法线的方向出现扩散。那么,自然地我们就想到,如果将待处理的像素置于滤波窗口的某个合适的边缘,使得滤波窗口尽可能地位于边缘的一侧,这样不就能够减轻甚至消除滤波窗口跨越边缘带来的影响了吗?这也正是作者在本文中提出的侧窗滤波技术(Side Window Filtering Technique)的核心思想,只不过作者在文中对侧窗的方向和尺寸选择作出了更加详尽的定义。
以下是对文中所述侧窗滤波技术的详细介绍。
如 Fig.4 所示,定义连续情况下的侧窗(Side Window),包含参数 $\theta $ 、 \(r\) 和 \(\rho\) 。其中,参数 \(\theta\) 是窗口与水平线的夹角,\(r\) 为窗口半径,\(\rho\) 作为控制窗口长度的另一参数且 \(\rho \in [0,r]\) 。规定 \((x,y)\) 为待处理像素(target pixel) i 的坐标。通过改变 \(\theta\) 的值我们便能控制窗口的朝向进而决定将窗口的哪一条边放在待处理像素之上。在 \(r\) 固定的情况下,控制 \(\rho\) 的大小就能控制窗口纵向的长度。
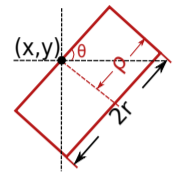
从上述定义中可以看出,对于某一像素 \((x, y)\) ,它的侧窗数量可以是无穷多个。但是在实际应用时,我们并不需要所有方向的窗口,一方面是由于当 \(\theta\) 取类似于 \(\frac{\pi}{4}\) 这样的角度时,倾斜的窗口并不利于我们做计算,另一方面,由于进行窗口运算的场景一般都是图像局部,属于一个比较小的范围,因此,我们只需要选取几个便于计算的特殊角度的窗口,然后再通过比较各个窗口处理的效果最终选出最合适的窗口即可。
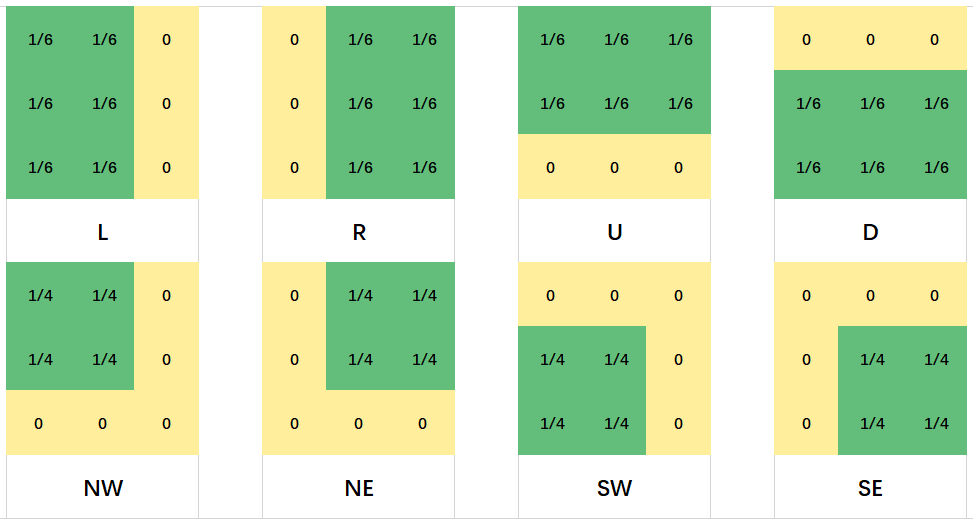
为了保证待处理像素 \((x, y)\) 一定位于窗口边缘或者边角处,作者在文中共定义了 8 类窗口,朝向分别定义为 L、R、U、D、NW、NE、SW、SE。这 8 类特定的窗口满足 \(\theta=k \times \frac{\pi}{2},k\in [0,3]\) 且 \(\rho = m \times r, m\in [0,1]\) ,如 Fig.5 所示。
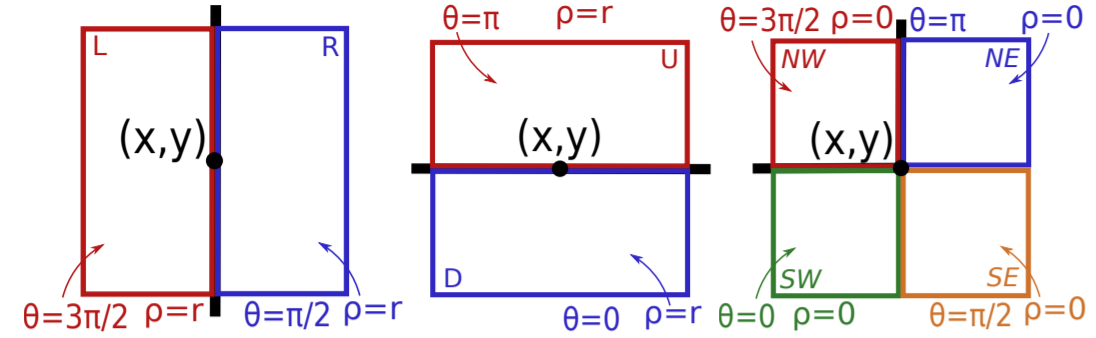
在完成这 8 类侧窗之后,我们需要设计一个算法对同一待处理像素在不同侧窗处理之后的效果进行评估,并找出最合适的侧窗类型。给出如下寻找最佳侧窗算法的定义:
算法1
-
假设像素 i 为待处理像素(target pixel),像素 j 为其邻接像素。 规定\(w_{ij}\) 为像素 j 基于侧窗核函数 \(F\) 给出的的对应权重,侧窗编组 \(S=\{L, R, U, D, N W, N E, S W, S E\}\) ;
-
定义 \(I_n\) 为待处理像素经不同侧窗 \(n\) 经加权滤波处理之后的结果,有:
\[I_{\mathrm{n}}=\frac{1}{N_{\mathrm{n}}} \sum_{j \in \omega_{\mathrm{n}}^{\mathrm{n}}} w_{i j} q_{j} \]其中,\(N_n\) 为单个侧窗的权重之和,即:
\[N_{\mathrm{n}}=\sum_{j \in \omega_{\mathrm{n}}^{\mathrm{n}}} w_{i j}, \mathrm{n} \in S \] -
定义代价函数 Ei:
\[E_i = \left\|q_{i}-I_{n}\right\|_{2}^{2} \]则最佳侧窗编号 \(I_m\) :
\[I_{m}= \operatorname{argmin}_{n \in S} E_i = \operatorname{argmin}_{n \in S}\left\|q_{i}-I_{n}\right\|_{2}^{2} \]上述算法的核心思想在于从 8 个结果中找出一个侧窗类型使得侧窗滤波结果尽可能地接近输入,以保证输出能够尽可能的保留原图像信息,一个比较好的办法就是求取两者之间的二范数。在找到这样的一个合适的侧窗后,便可以将其滤波结果作为最终的侧窗滤波结果,达到保边的效果。
实验结果与分析
1. 侧窗技术应用 -- 均值滤波理论分析
1.1 多类边缘均值滤波结果对比
为便于分析,将侧窗技术应用在均值滤波之上,并作用于六类典型边缘图像(这里作者写的是 Box Filter,但是根据 1.2 节验证时的最终计算结果来看,作者采用的更准确地来说应该是 Mean Filter,故以下均视作均值滤波进行讨论)。如 Fig.6 所示,其中第 1 列和第 4 列为六种典型边缘图像,第 2 列和第 4 列为输入图像正中心那一行像素的像素值情况及两种均值滤波的结果,第 3 列和第 5 列为边缘处的局部放大图。
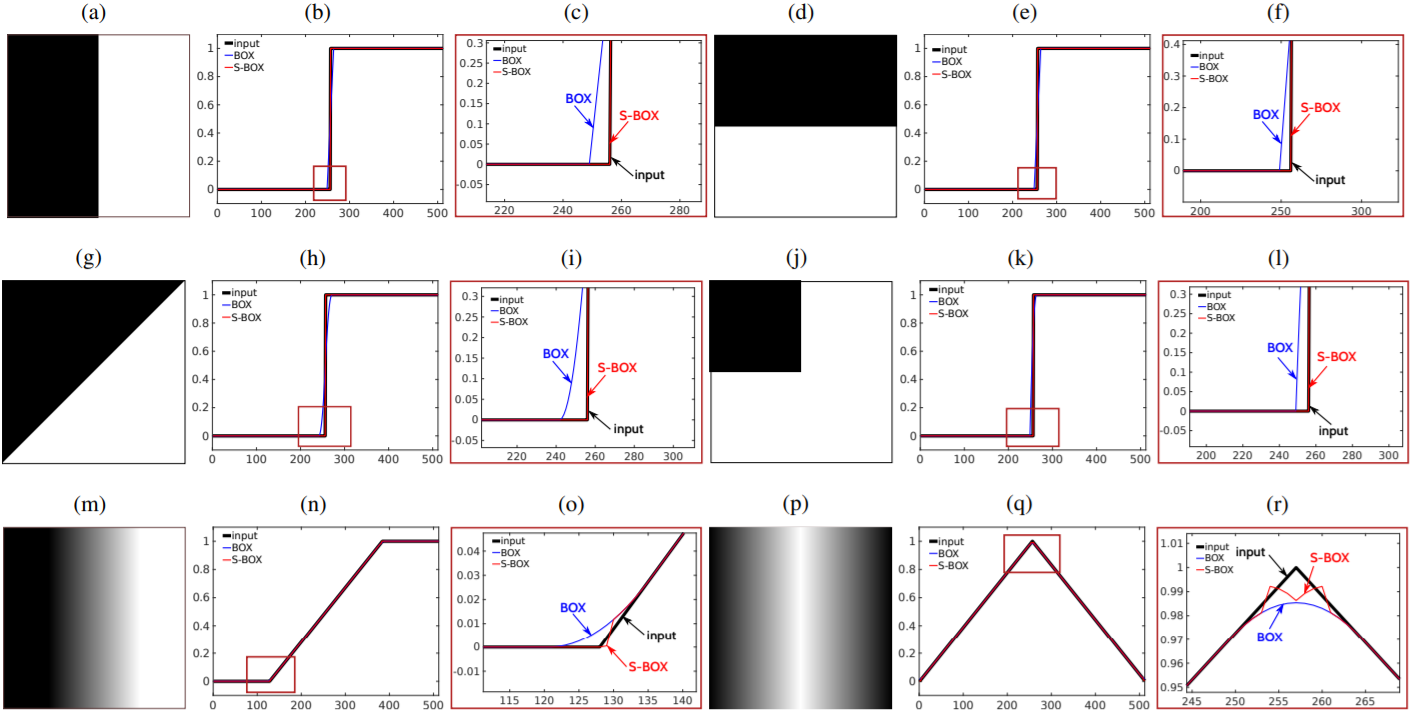
1.2 竖直边缘图像理论分析
为了验证侧窗均值滤波技术确实如作者所述的那样比传统均值滤波技术要好,现对存在竖直边缘的图像做计算分析。以下图为例,图中存在一竖直边缘,规定边缘左侧的深色区域像素值为 u ,右侧的白色趋于像素值为 v ,取黑白交界处的某一像素 i 为待处理像素。如 Fig.7 所示:

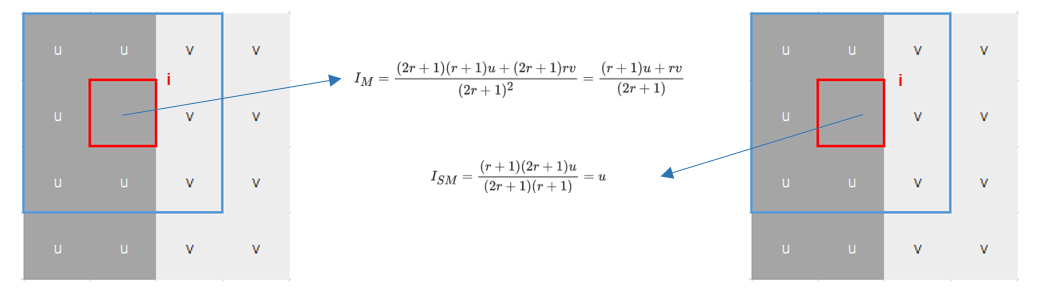
将传统均值滤波和侧窗均值滤波分别作用于像素 i ,两窗口滤波核半径均为 2r+1,其中侧窗均值滤波以左窗口 L 为例,如 Fig.8 所示。需要注意侧窗均值滤波的滤波核只计算侧窗内的均值。
使用两种核对像素 i 进行操作,可以得到如 Fig.9 的结果,其中左图 \(I_M\) 表示传统均值滤波结果,右图 \(I_{SM}\) 表示侧窗均值滤波结果:
比较该像素经两种方式滤波之后的代价
传统均值滤波:
侧窗均值滤波
显然可知 \(E_{iM} > E_{iSM}\)
更一般地,计算对像素 i 共计 8 个方向的侧窗均值滤波结果如下:

运用算法1,可以直接选取 侧窗 L 的计算结果为最终滤波结果。从结果上来看,侧窗均值滤波的损失代价确实小于传统均值滤波。
2. 侧窗技术应用 -- 滤波算法复现
2.1 软硬件参数
- 处理器:Intel(R) Core (TM) i5-7400 CPU @ 3.00GHz
- RAM内存大小:16GB
- 集显:Intel(R) HD Graphics 630
- 独显:NVIDIA GeForce GTX1050
- 操作系统:Windows 10
- 开发语言:Python
- 程序依赖库版本:Python-3.7.3,Open-CV-4.2.0,Scipy-1.4.1,Numpy-1.18.4
2.2 侧窗均值滤波算法复现
2.2.1 程序思想
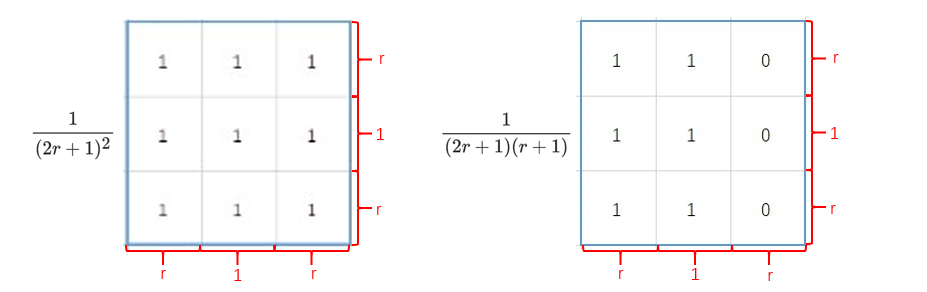
首先需要定义 8 个方向的侧窗核,而对于均值计算来说,可以视作核与图像子区域的滑动卷积。因此,可以将 8 类核统一定义为尺寸一致,但是核内权重不同的核,方便之后之间直接采用矩阵卷积计算。以核半径 \(r = 1\) 为例,8 类 3x3 的核样式如 Fig.10 所示。
其次,需要将输入图像进行色彩通道分离。为了保证图像边缘的信息不丢失,还需要对各通道图像边缘进行填充,填充半径增量均为 r ,填充内容与边缘像素值保持一致,如 Fig.11 所示。
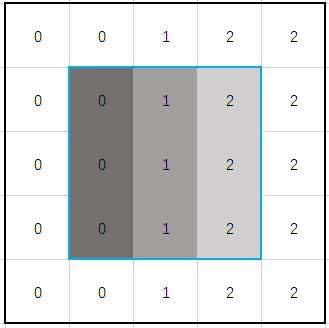
- 然后,将 8 类滤波核作用于与填充之后的单通道图像作卷积运算。在得到 8 组均值滤波后的结果之后,计算他们与该通道原图之间的差值,取绝对值作为损失,通过比较 8 组损失,挑选出损失最小的那一组最为该通道最佳的滤波结果。其余 2 个通道做法同理。除此之外,设置迭代次数可实现多次滤波处理。
最后,将滤波之后的 3 个通道图像进行合并,并裁去开始填充的边缘,得到最终的处理结果。
2.2.2 效果展示
输入测试图像 1 尺寸为 270x180x3,添加比重为 0.02 的椒盐噪声,结果如 Fig.12 所示。
 |
 |
|---|---|
| (a) 原图 | (b) 添加噪声后的图像 |
对 Fig.12 (b) 做若干次传统均值滤波处理(以下简称传统处理),滤波核大小为 7x7,迭代次数分别为 1 次、5 次和 10 次,结果如Fig.13:
 |
 |
 |
|---|---|---|
| (a) 传统均值滤波(1次) | (b) 传统均值滤波(5次) | (c) 传统均值滤波(10次) |
对 Fig.12 (b) 做若干次侧窗均值滤波处理(以下简称侧窗处理),滤波核大小为 7x7,迭代次数分别为 1 次、5 次和 10 次,结果如 Fig.14:
 |
 |
 |
|---|---|---|
| (a) 侧窗均值滤波(1次) | (b) 侧窗均值滤波(5次) | (c) 侧窗均值滤波(10次) |
对比两组结果可以发现,在同样迭代 1 次的情况下,传统处理与侧窗处理均只能在一定程度上减轻椒盐噪声的影响,不同之处在于传统处理之后的图像已经发生了比较明显的边缘模糊现象,而侧窗处理则较好的保留了边缘信息。进一步的,随着迭代次数的增加,两者均消除了大部分的椒盐噪声,但是此时经传统处理的图像已经出现了严重的失真,而测窗处理之后的图像边缘却依然能够很好地分辨。
我们将两种算法处理 10 次 之后的结果进行局部放大,如 Fig.15所示,可以发现经侧窗处理 10 次之后的动物胡须仍旧清晰可见。
 |
 |
|---|---|
| (a) 传统均值滤波(10次)及局部放大图 | (b) 侧窗均值滤波(10次)及局部放大图 |
2.3 侧窗中值滤波算法复现
2.3.1 算法思想
与侧窗均值滤波算法类似,同样需要定义 8 个不同方向的侧窗核。由于中值滤波是一类非线性逼近的图像滤波操作,即不需要图像像素参与数学运算,而是参与数值排序,因此对于我们需要的不是侧窗核内部的权重信息,而是侧窗核的尺寸分布信息。因此我们将 Fig.10 的均值侧窗核做些许改动,结果如 Fig.13 所示,其中 1 表示该位置的图像像素参与排序,0 表示不参与排序。
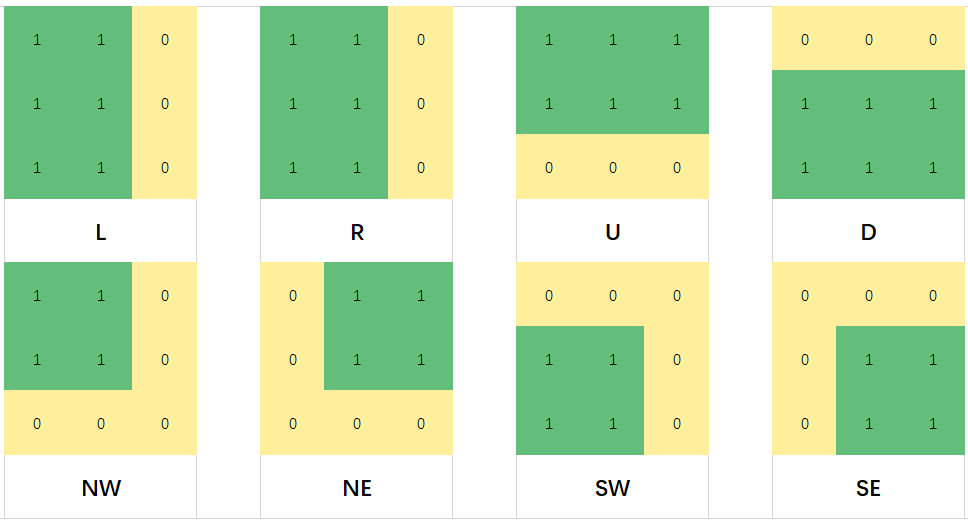
实际编程实现的时候,将侧窗核中的 0 省去,使 8 个侧窗核形状不尽相同,为核窗口的滑动始末位置添加行列偏移量的方式来控制不同尺寸的侧窗核的滑动范围。以半径 r = 1,尺寸为 3x3 标准大小的滤波核为例,侧窗核 SE 位于其右下角,且所占控件大小为 2x2 ,因此在实际滤波过程中单幅图像的前 r 行和前 r 列是一定不会参与侧窗核 SE 的操作的,因此核 SE 的起始行列偏移量可记为 \((r,r)\) ,而终止行列偏移量为 \((0,0)\) ,其余 7 个侧窗核类似,总结如下表:
| 侧窗核 | L | R | U | D | NW | NE | SW | SE |
|---|---|---|---|---|---|---|---|---|
| 尺寸 | (2r+1)x(r+1) | (2r+1)x(r+1) | (r+1)x(2r+1) | (r+1)x(2r+1) | (r+1)x(r+1) | (r+1)x(r+1) | (r+1)x(r+1) | (r+1)x(r+1) |
| 起始行列偏移量 | (0,0) | (0,r) | (0,0) | (r,0) | (0,0) | (0,r) | (r,0) | (r,r) |
| 终止行列偏移量 | (0,r) | (0,0) | (r,0) | (0,0) | (r,r) | (r,0) | (0,r) | (0,0) |
完成 8 个方向的侧窗核定义之后,剩下的操作与侧窗均值滤波类似,不同之处只在于将取均值操作变成取中值操作。
2.3.2 效果展示
使用与 2.2.2 节测试完全相同的图片,也添加比重为 0.02 的椒盐噪声。如 Fig.12 所示。
对 Fig.12 (b) 做若干次传统中值滤波处理,滤波核大小为 7x7,迭代次数分别为 1 次、5 次和 10 次,结果如Fig.16:
 |
 |
 |
|---|---|---|
| (a) 传统中值滤波(1次) | (b) 传统中值滤波(5次) | (c) 传统中值滤波(10次 |
对 Fig.12 (b) 做若干次侧窗中值滤波处理,滤波核大小为 7x7,迭代次数分别为 1 次、5 次和 10 次,结果如Fig.17:
 |
 |
 |
|---|---|---|
| (a) 侧窗中值滤波(1次) | (b) 侧窗中值滤波(5次) | (c) 侧窗中值滤波(10次) |
| Fig.17 |
同样地,对比两组结果可以发现,相较于传统中值滤波处理来说,侧窗中值滤波处理过后的图像在滤除绝大部分噪声的同时,更好地保留了图像的边缘信息。
2.5 侧窗高斯滤波算法复现
这部分由于当时写的时候遇到了点问题滤波效果一直不好,因此没有加到课程报告里。后来报告提交之后,突然意识到是因为自己没有对滤波核内的权值进行归一化,于是进行了修改,程序放在了最后,测试结果就懒得再去测了 hhhh
3. 算法复现效果评价
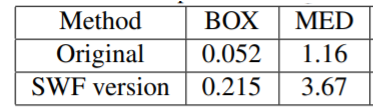
从上述两组实验中可以看出,复现的侧窗滤波算法在一定程度上已经满足了与作者文中所述的保边效果。但是,正如作者最后所提到的算法复杂度分析,由于侧窗滤波算法需要对多类窗口进行运算,因此它需要花费更高的时间代价。表 3 为两组实验中单张图像处理平均耗时的统计结果,表 4 为作者在文中统计的结果。对比本实验复现的侧窗滤波算法与作者实现的结果,可以发现对于均值滤波算法,本实验中复现的结果从与传统处理速度的倍数关系上来说,已接近作者的实验结果,但是本实验中复现的中值滤波算法却表现出较差的性能,因此需要进一步的代码优化。
| 方法 | 均值滤波 | 中值滤波 |
|---|---|---|
| 传统方法 | 0.1441 s | 0.0059 s |
| 侧窗技术 | 0.7557 s | 4.8879 s |
总结与展望
除了上述的均值滤波和中值滤波之外,侧窗技术还可以应用于更多种类的滤波算法中,比如高斯滤波、双边滤波等等。利用这些改进后的滤波算法,可以对图像进行更加优良地图像降噪、图像平滑、图像增强。



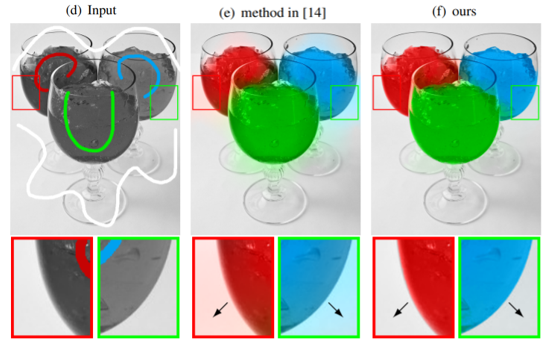
进一步地,侧窗技术在 HDR 色调映射方面也表现出了更好的性能。

除此之外,侧窗技术还可应用于自然图像的结构保留和纹理去除(Structure-preserving and texture-removing on natural image)、图像相同结构的提取(Mutual structure extraction)以及图像上色等领域。

 |
 |
|---|---|
因此,不难发现,这篇论文中所提出的 Side Window Filtering 技术看起来仅仅是将待处理像素放到了滤波窗口的边缘,但是却使得众多基础滤波算法的保边性能得到了较大的提升。不仅如此,我认为这一算法不仅可以运用在图像处理领域,甚至可以将其思想运用在类似于卷积神经网络这样的需要利用卷积核提取图像信息的领域,也许会获得意想不到的效果。不过当前算法存在的最大的一个问题就是处理速度,从之前的实验也可以发现相较于传统处理,它至少多出了 3 倍以上的时间损耗。对于盒子滤波来说,已经存在能够快速计算的改进算法了,但是对于其他的滤波算法,还需要进行更加深入的研究。相信一旦计算速度的问题被解决,此项技术必定能够在计算机视觉领域大放异彩!
参考文献
[1]Yin H, Gong Y, Qiu G. Side window filtering[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 8758-8766.
作者在知乎上的论文简介:CVPR2019 Oral论文 #5176 Side Window Filtering介绍
另外一个博主用C++ 复现的:Side Window Filtering 论文解读和C++实现
[2]J. Anaya and A. Barbu. Renoir - a dataset for real low-light image noise reduction. Journal of Visual Comm. and Image Rep, 51(2):144–154, 2018.
[3]H. Chidiac and D. Ziou. Classification of image edges. Vision Interface
[4]Paul Viola,Michael Jones.Rapid Object Detection using a Boosted Cascade of Simple Features[C].//2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'01), vol.1.2001:511-518.
[5]Xiaoyong Shen,Chao Zhou,Li Xu, et al.Mutual-Structure for Joint Filtering[J].International Journal of Computer Vision,2017,125(1/3):19-33.
程序开源
写得比较仓促,所以也没有对程序进行进一步的优化,测试代码直接就随便写了点,感兴趣的可以加以改造~
Github 托管地址:Side_Window_Filtering


