递归的思想
以此类推是递归的基本思想。
具体来讲就是把规模大的问题转化为规模小的相似的子问题来解决。在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况。另外这个解决问题的函数必须有明显的结束条件,这样就不会产生无限递归的情况了。
递归的两个条件
- 可以通过递归调用来缩小问题规模,且新问题与原问题有着相同的形式。(自身调用)
- 存在一种简单情境,可以使递归在简单情境下退出。(递归出口)
递归算法的一般形式:
|
1
2
3
4
5
6
7
|
func( mode){ if(endCondition){ //递归出口 end; }else{ func(mode_small) //调用本身,递归 }} |
求一个数的阶乘是练习简单而典型的例子,阶乘的递推公式为:factorial(n)=n*factorial(n-1),其中n为非负整数,且0!=1,1!=1
我们根据递推公式可以轻松的写出其递归函数:
|
1
2
3
4
5
6
7
8
|
public static long factorial(int n) throws Exception { if (n < 0) throw new Exception("参数不能为负!"); else if (n == 1 || n == 0) return 1; else return n * factorial(n - 1);} |
递归的过程
在求解6的阶乘时,递归过程如下所示。

我们会惊奇的发现这个过程和栈的工作原理一致对,递归调用就是通过栈这种数据结构完成的。整个过程实际上就是一个栈的入栈和出栈问题。然而我们并不需要关心这个栈的实现,这个过程是由系统来完成的。
那么递归中的“递”就是入栈,递进;“归”就是出栈,回归。
我们可以通过一个更简单的程序来模拟递进和回归的过程:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
/** * 关于 递归中 递进和回归的理解 * @param n */public static void recursion_display(int n) { int temp=n;//保证前后打印的值一样 System.out.println("递进:" + temp); if (n > 0) { recursion_display(--n); } System.out.println("回归:" + temp);} |
递归的例子
斐波那契数列
斐波那契数列的递推公式:Fib(n)=Fib(n-1)+Fib(n-2),指的是如下所示的数列:
1、1、2、3、5、8、13、21.....
按照其递推公式写出的递归函数如下:
|
1
2
3
4
5
6
7
8
|
public static int fib(int n) throws Exception { if (n < 0) throw new Exception("参数不能为负!"); else if (n == 0 || n == 1) return n; else return fib(n - 1) + fib(n - 2);} |
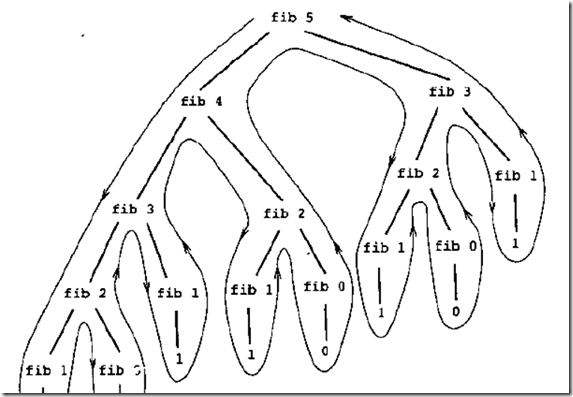
递归调用的过程像树一样,通过观察会发现有很多重复的调用。
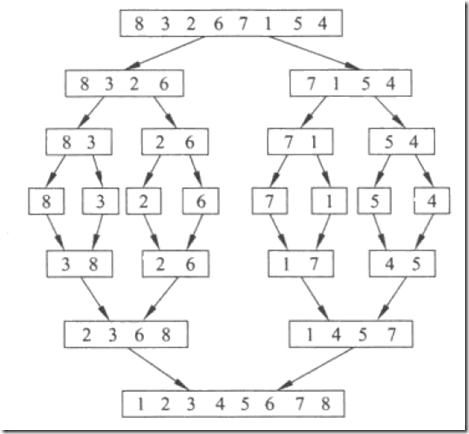
归并排序
归并排序也是递归的典型应用,其思想:将序列分为若干有序序列(开始为单个记录),两个相邻有序的序列合并成一个有序的序列,以此类推,直到整个序列有序。
|
1
2
3
4
5
6
7
8
9
10
11
|
//递归过程是:在递进的过程中拆分数组,在回归的过程合并数组public static void mergeSort(int[] source, int[] temp, int first, int last) { if (first < last) { int mid = (first + last) / 2; mergeSort(source, temp, first, mid); //归并排序前半个子序列 mergeSort(source, temp, mid + 1, last); //归并排序后半个子序列 merge(source, temp, first, mid, last); //在回归过程中合并 } else if (first == last) { //待排序列只有一个,递归结束 temp[first] = source[first]; }} |
同样调用过程向树一样,但是它并没有重复调用的问题。在递进的过程中拆分数组,在回归的过程合并数组 。通过递归来实现归并排序,程序结构和条理非常清晰。