题意简述
一个长度为 \(n\) 的序列,每一个位置 \(i\) 有两个属性值 \(a_i,b_i\) 。
有 \(q\) 次询问,形如 \(l,r,c,d\) ,查询有多少个 \(i\) 满足 \(i\in [l,r],(a_i\oplus c)\le \min\{b_i,d\}\) ,其中 \(\oplus\) 为按位异或运算。
\(1\le n,q\le 10^5\ ,\ 1\le l\le r\le n\ ,\ 0\le a_i,b_i,c,d<2^{24}\)。
算法分析
首先暴力特别好写,复杂度 \(\mathcal O(nq)\) (然后就可以用指令集优化了,暴力碾标算)。
先考虑一个部分分,\(\max\{d\}\le \min\{b_i\}\),即我们只需要考虑 \(d\) 的限制。这是一道原题。
限制是异或,因此考虑按位分析。我们从高位到低位遍历,考虑第 \(p\) 位,分两种情况:
- \(d_p=0\) ,此时如果在考虑的范围内 \((a_i\oplus c)_p=1\),则一定不合法,即必须满足 \((a_i\oplus c)_p=0\) 但仍然不确定,因此需继续遍历低位;
- \(d_p=1\) ,此时如果在考虑的范围内 \((a_i\oplus c)_p=0\),则一定合法,无需继续遍历,否则不确定,需继续遍历低位。
这种限制条件很容易用 0-1 trie 表示出,即:
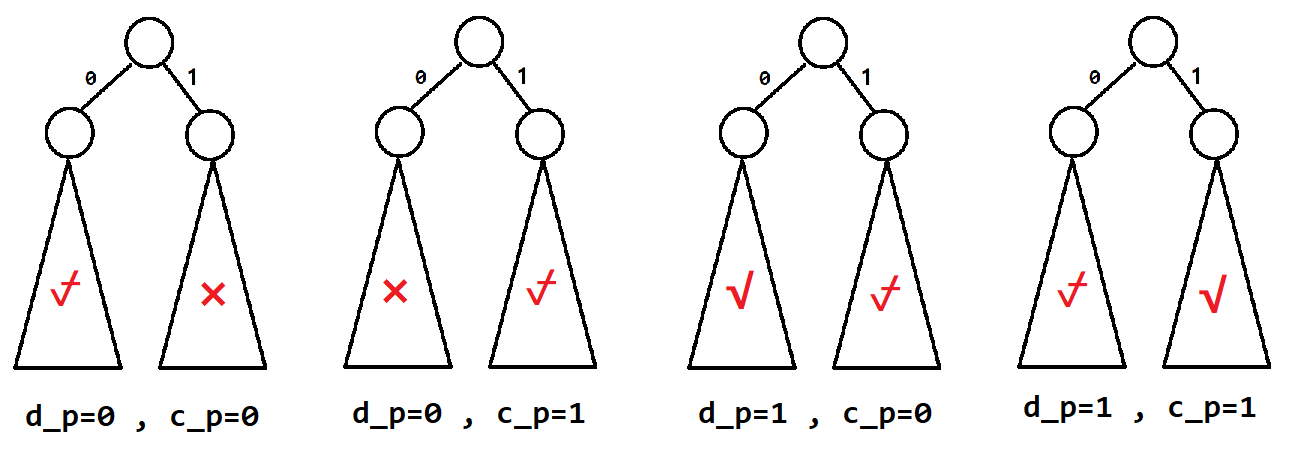
把 \(a_i\) 插入 trie 即可,为了处理 \(i\in [l,r]\) 的限制,要使用可持久化 trie ,时空复杂度均为 \(\mathcal O(n\log n)\) 。
再考虑第二个部分分,\(\max\{b_i\}\le \min\{d\}\),即我们只需要考虑 \(b_i\) 的限制。此时插入的有两个限制,询问只有一个限制,因此考虑反过来计算贡献,如下分析:
继续从高位到低位遍历,考虑第 \(p\) 位,分两种情况:
- \(b_p=0\) ,此时如果在考虑的范围内询问的 \(c\) 会使得 \((a_i\oplus c)_p=1\) 成立,则一定不合法,即必须满足 \((a_i\oplus c)_p=0\) ,这个元素才有可能给询问 \(c\) 一个贡献,但仍然不确定,因此需继续遍历低位;
- \(b_p=1\) ,此时如果在考虑的范围内询问的 \(c\) 会使得 \((a_i\oplus c)_p=0\),则一定合法,一定有贡献,无需继续遍历,否则不确定是否产生贡献,需继续遍历低位。
这种限制条件是类似的,也可以用 0-1 trie 表示出,即:
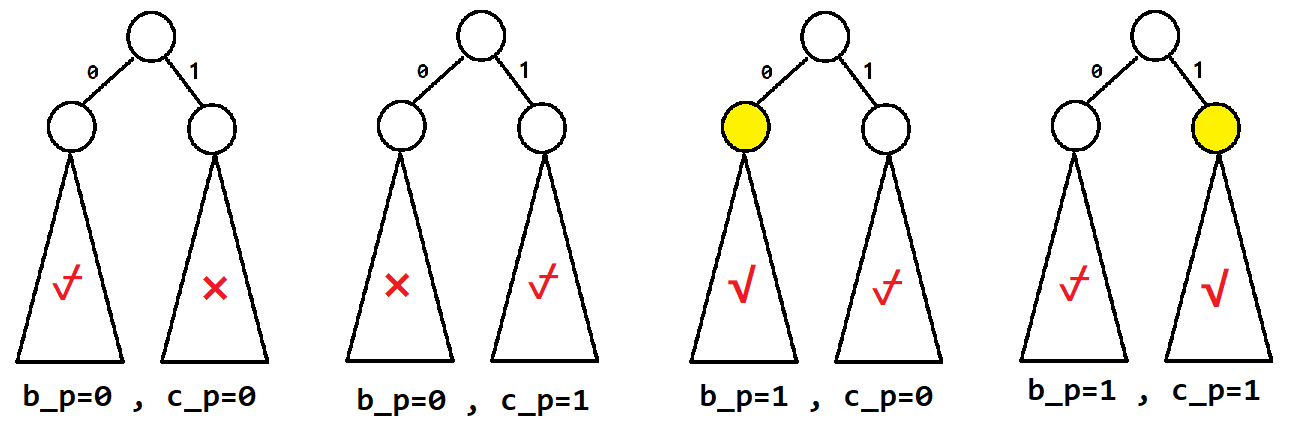
其中黄色节点表示此处有贡献,最后询问的时候把经过的所有点的贡献相加即为答案。
同样使用可持久化 trie 维护下标偏序关系,时空复杂度均为 \(\mathcal O(n\log n)\) 。
两者结合,我们很难同时考虑两个限制。不妨找到一个分界,前面的所有元素满足 \(b_i<d\) ,后面的所有元素满足 \(b_i>d\) 。我们按照 \(b,d\) 升序排序后 two pointers 扫一遍即可求解。
但是由于排序的存在,我们无法继续沿用可持久化 trie 的方法处理下标偏序关系。由于信息可加可减,因此有如下两种解决方案:
- 树状数组套
trie,时空复杂度均为 \(\mathcal O(n\log^2 n)\),空间卡不过去。 cdq分治套trie,时间复杂度 \(\mathcal O(n\log^2 n)\) ,空间复杂度 \(\mathcal O(n\log n)\),可以卡过去。
树状数组套 trie 直接维护 \(n\) 棵 trie,外层树状数组维护其维护区间的所有元素的 trie 的根,修改直接暴力插入即可,比较直观,也比较无脑。
cdq分治 套 trie,在外层把下标限制拆开,按照下标排序,内层再按照 \(b_i/d\) 排序,左边修改对右边询问产生贡献,实现起来有一些细节。
代码实现
树状数组套 trie,(luogu民间数据只有20分,沦为暴力……)
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 20000005
#define inf 0x3f3f3f3f
#define LL long long
#define ull unsigned long long
#define ldb long double
#define mod 1000000007
#define eps 1e-9
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp> void read(Tp &x){
int fh=1;char c=getchar();x=0;
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c&15);c=getchar();}x*=fh;
}
int n,m;
struct node{
int id,a,b;
bool operator <(node y)const{
return b<y.b;
}
};
struct Quer{
int id,l,r,c,d;
bool operator <(Quer y)const{
return d<y.d;
}
};
node ai[maxn];
Quer qi[maxn];
int ans[maxn];
namespace Sub1{//d<b chk d
int ch[maxm][2],siz[maxm],T[maxn],tot;
void upd(int rt,int x,int v){//情况1的插入
int p=rt,dir;
for(int i=23;~i;--i){
dir=((x>>i)&1);
if(!ch[p][dir])ch[p][dir]=++tot;
p=ch[p][dir];
siz[p]+=v;//记录个数
}
}
int query(int rt,int c,int d){//情况1的查询
++d;//这里要+1,因为我们上面的分析过程没有计算本身,这样写能减少边界细节
int ret=0,p=rt,dc,dd;
for(int i=23;~i;--i){
dc=((c>>i)&1);dd=((d>>i)&1);
if(dd){
ret+=siz[ch[p][dc]];//累加确定的个数
p=ch[p][dc^1];
}
else p=ch[p][dc];
if(!p)break;
}
return ret;
}
void add(int x,int a,int v){//树套树修改
for(;x<=n;x+=(x&(-x))){
upd(T[x],a,v);
}
}
int ask(int x,int c,int d){//树套树查询
int ret=0;
for(;x;x-=(x&(-x)))ret+=query(T[x],c,d);
return ret;
}
void prep(){
for(int i=1;i<=n;++i)T[i]=++tot;
for(int i=1;i<=n;++i)add(ai[i].id,ai[i].a,1);
}
}
namespace Sub2{// d>b chk b
int ch[maxm][2],siz[maxm],T[maxn],tot;
void upd(int rt,int a,int b,int v){//情况2的插入
++b;//这个细节与上面的同理
int p=rt,da,db;
for(int i=23;~i;--i){
da=((a>>i)&1);db=((b>>i)&1);
if(db){
if(!ch[p][da])ch[p][da]=++tot;
if(!ch[p][da^1])ch[p][da^1]=++tot;
siz[ch[p][da]]+=v;//记录贡献
p=ch[p][da^1];
}
else{
if(!ch[p][da])ch[p][da]=++tot;
p=ch[p][da];
}
}
}
int query(int rt,int c){//情况2的查询
int p=rt,ret=0,dir;
for(int i=23;~i;--i){
dir=((c>>i)&1);
if(!ch[p][dir])break;
p=ch[p][dir];ret+=siz[p];//累加贡献
}
return ret;
}
void add(int x,int a,int b,int v){
for(;x<=n;x+=(x&(-x))){
upd(T[x],a,b,v);
}
}
int ask(int x,int c){
int ret=0;
for(;x;x-=(x&(-x)))ret+=query(T[x],c);
return ret;
}
void prep(){
for(int i=1;i<=n;++i)T[i]=++tot;
}
}
//其实两个情况的代码十分类似,第一个的插入与第二个的询问几乎一样,第一个的询问与第二个的插入几乎一样,
signed main(){
#ifndef local
file("island");
#endif
read(n);read(m);
for(int i=1;i<=n;++i){
read(ai[i].a);read(ai[i].b);ai[i].id=i;
}
for(int i=1;i<=m;++i){
read(qi[i].l);read(qi[i].r);read(qi[i].c);read(qi[i].d);qi[i].id=i;
}
sort(ai+1,ai+n+1);
sort(qi+1,qi+m+1);
Sub1::prep();
Sub2::prep();
for(int i=1,j=1;i<=m;++i){
while(j<=n&&ai[j].b<qi[i].d){//two pointers扫描
Sub1::add(ai[j].id,ai[j].a,-1);
Sub2::add(ai[j].id,ai[j].a,ai[j].b,1);
++j;
}
int t1=Sub1::ask(qi[i].r,qi[i].c,qi[i].d);
int t2=Sub1::ask(qi[i].l-1,qi[i].c,qi[i].d);
int t3=Sub2::ask(qi[i].r,qi[i].c);
int t4=Sub2::ask(qi[i].l-1,qi[i].c);
ans[qi[i].id]=(t1-t2)+(t3-t4);//代价相减,统计总和
}
for(int i=1;i<=m;++i)printf("%d\n",ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}
cdq分治 套 trie(luogu民间数据能 AC)
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 10000005
#define inf 0x3f3f3f3f
#define LL long long
#define ull unsigned long long
#define ldb long double
#define mod 1000000007
#define eps 1e-9
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp> void read(Tp &x){
int fh=1;char c=getchar();x=0;
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c&15);c=getchar();}x*=fh;
}
int n,m,nm;
struct Oper{
int id,ps,typ,a,b,c,d;//为了能够cdq,这里做了比较大的改版
bool operator <(Oper y)const{
if(ps==y.ps){
if(!typ||!y.typ)return !typ;
else return typ<y.typ;
}
else return ps<y.ps;
}
};
bool cmp1(Oper x,Oper y){
return x.b<y.b;
}
Oper ai[maxn];
int ans[maxn];
namespace Sub1{//d<b chk d
int ch[maxm][2],siz[maxm],RT,tot;
void upd(int x,int v){
int p=RT,dir;
for(int i=23;~i;--i){
dir=((x>>i)&1);
if(!ch[p][dir])ch[p][dir]=++tot;
p=ch[p][dir];
siz[p]+=v;
}
}
int query(int c,int d){
++d;
int ret=0,p=RT,dc,dd;
for(int i=23;~i;--i){
dc=((c>>i)&1);dd=((d>>i)&1);
if(dd){
ret+=siz[ch[p][dc]];
p=ch[p][dc^1];
}
else p=ch[p][dc];
if(!p)break;
}
return ret;
}
void prep(){RT=tot=1;}
}
namespace Sub2{// d>b chk b
int ch[maxm][2],siz[maxm],RT,tot;
void upd(int a,int b,int v){
++b;
int p=RT,da,db;
for(int i=23;~i;--i){
da=((a>>i)&1);db=((b>>i)&1);
if(db){
if(!ch[p][da])ch[p][da]=++tot;
if(!ch[p][da^1])ch[p][da^1]=++tot;
siz[ch[p][da]]+=v;
p=ch[p][da^1];
}
else{
if(!ch[p][da])ch[p][da]=++tot;
p=ch[p][da];
}
}
}
int query(int c){
int p=RT,ret=0,dir;
for(int i=23;~i;--i){
dir=((c>>i)&1);
if(!ch[p][dir])break;
p=ch[p][dir];ret+=siz[p];
}
return ret;
}
void prep(){RT=tot=1;}
}
//两个情况与树套树做法几乎一模一样,唯一的不同是只有一棵树,没有外层的树状数组结构
void cdq(int l,int r){
if(l==r)return;
int mid=((l+r)>>1);
cdq(l,mid);cdq(mid+1,r);
sort(ai+l,ai+mid+1,cmp1);sort(ai+mid+1,ai+r+1,cmp1);//这里可以写归并优化常数
for(int i=l;i<=mid;++i){
if(!ai[i].typ){
Sub1::upd(ai[i].a,1);
}
}
int j=l;
for(int i=mid+1;i<=r;++i){
while(j<=mid&&ai[j].b<ai[i].d){//同样 two pointers计算贡献
if(!ai[j].typ){
Sub1::upd(ai[j].a,-1);
Sub2::upd(ai[j].a,ai[j].b,1);
}
++j;
}
if(ai[i].typ){
int t1=Sub1::query(ai[i].c,ai[i].d);
int t2=Sub2::query(ai[i].c);
ans[ai[i].id]+=ai[i].typ*(t1+t2);//因为询问的[l,r]拆解,这里要乘上系数
}
}
for(int i=l;i<j;++i){//记得 全 部 清 空
if(!ai[i].typ){
Sub2::upd(ai[i].c,ai[i].d,-1);
}
}
for(int i=j;i<=mid;++i){
if(!ai[i].typ){
Sub1::upd(ai[i].a,-1);
}
}
}
signed main(){
#ifndef local
file("island");
#endif
read(n);read(m);
for(int i=1,a,b;i<=n;++i){
read(a);read(b);
ai[++nm]=(Oper){i,i,0,a,b,a,b};
}
for(int i=1,l,r,c,d;i<=m;++i){
read(l);read(r);read(c);read(d);
ai[++nm]=(Oper){i,r,1,c,d,c,d};
ai[++nm]=(Oper){i,l-1,-1,c,d,c,d};
}
sort(ai+1,ai+nm+1);
Sub1::prep();Sub2::prep();
cdq(1,nm);
for(int i=1;i<=m;++i)printf("%d\n",ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号