AGC035C题解

题意简述

构造一棵 \(2n\) 个点的树，第 \(i\) 个点和第 \(i+n\) 个点的权值都是 \(i\) ，并且第 \(i\) 个点到第 \(i+n\) 个点的路径上点的权值异或和为 \(i\)。

\(1\le n\le 10^5\)。

算法分析

首先这题无解很好判断，如果 \(n=2^k,k\in N\)，则 \(n\) 和 \(2n\) 之间没没有点能把最高位异或掉，因此路径一定非法，一定无解。

下面考虑对其余情况进行构造。

样例给了一个 \(n=3\) 的构造，其结构比较简单（1-2-3-1-2-3），我们考虑以此为基础构造。

因为利用(1-2-3-1-2-3)我们可以构造出后两位的任意情况，所以考虑按模4剩余类分类讨论。

1. \(n=4k+3\)
   如下图构造即可：
   

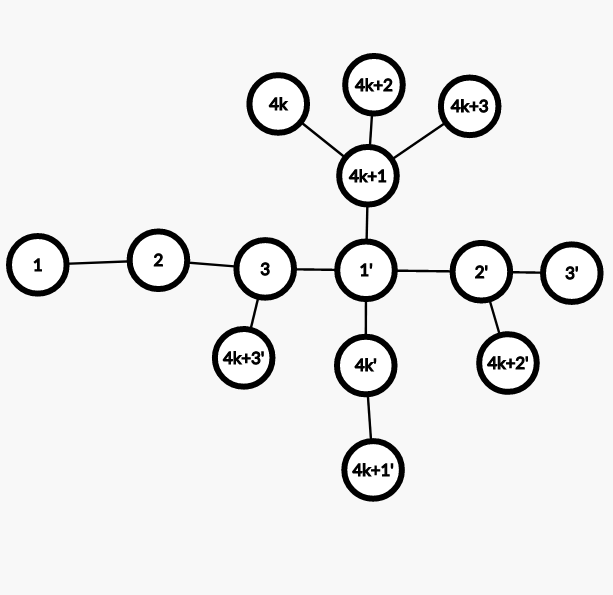
由上图我们不难发现因为彼此独立，我们现在的构造也能处理 \(n=4k+2,n=4k+1\) 的情况，下面不再讨论。

2. \(n=4k\)
   其实主要就是考虑最后一个点怎么放。

如果 \(n=4\) 显然无解。

否则找 \(n\) 的 lowbit（记为 \(t\) ），在1'的上面找到对应节点 \(x_1\) 满足 \(x_1\ \mathrm{xor}\ 1=t\) ，在1'的下面找对应节点 \(x_2\) 满足 \(x_2\ \mathrm{xor}\ t=n\)。将 \(n,n'\) 分别和 \(x_1,x_2\) 连边即可。可以证明 \(x_1,x_2<n\)，因此一定存在节点。

代码实现

#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp> void read(Tp &x){
	int fh=1;char c=getchar();x=0;
	while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c&15);c=getchar();}x*=fh;
}
int n,m;
signed main(){
	read(n);
	if((n&(-n))==n)puts("No");//n=2^k无解
	else{
		puts("Yes");
		printf("%d %d\n",1,2);
		printf("%d %d\n",2,3);
		printf("%d %d\n",3,n+1);
		printf("%d %d\n",n+1,n+2);
		printf("%d %d\n",n+2,n+3);//构造好3的基础
		int mdl=n%4;
		for(int i=4;i<=n-4;i+=4){//每4个一组，按第一类连边
			printf("%d %d\n",i,i+1);
			printf("%d %d\n",i+2,i+1);
			printf("%d %d\n",i+3,i+1);
			printf("%d %d\n",i+1,n+1);
			printf("%d %d\n",n+1,i+n);
			printf("%d %d\n",i+n,i+n+1);
			printf("%d %d\n",n+2,n+i+2);
			printf("%d %d\n",3,n+i+3);
		}
		if(mdl==0){//第二种情况
			int tt=(n&(-n));
			int tmp=(n^tt);
			printf("%d %d\n",n,tt|1);
			printf("%d %d\n",2*n,tmp+n);
		}
		if(mdl==1){//第一种情况 n=4k+1
			int i=n-1;
			printf("%d %d\n",i,i+1);
			printf("%d %d\n",i+1,n+1);
			printf("%d %d\n",i+n,i+n+1);
			printf("%d %d\n",n+1,i+n);
		}
		if(mdl==2){//第一种情况 n=4k+2
			int i=n-2;
			printf("%d %d\n",i,i+1);
			printf("%d %d\n",i+2,i+1);
			printf("%d %d\n",i+1,n+1);
			printf("%d %d\n",i+n,i+n+1);
			printf("%d %d\n",n+1,i+n);
			printf("%d %d\n",n+2,n+i+2);
		}
		if(n>3&&mdl==3){//第一种情况 n=4k+3
			int i=n-3;
			printf("%d %d\n",i,i+1);
			printf("%d %d\n",i+2,i+1);
			printf("%d %d\n",i+3,i+1);
			printf("%d %d\n",i+1,n+1);
			printf("%d %d\n",i+n,i+n+1);
			printf("%d %d\n",n+1,i+n);
			printf("%d %d\n",n+2,n+i+2);
			printf("%d %d\n",3,n+i+3);
		}
	}
	return 0;
}