比赛情况:100+100+30+100,rk8。
好像前16中就我一个第三题没有切掉……
A 牛牛的方程式
题意简述
给定 \(a,b,c,d\) ,询问是否存在一组整数解 \(x,y,z\) ,满足 \(ax+by+cz=d\) 。
多测, \(-10^{18}\le a,b,c,d\le 10^{18},1\le T\le 100\) 。
算法标签
数论 同余
算法分析
如果只有两项,即 \(ax+by=c\) 这种形式,可以直接套用裴蜀定理,该方程有整数解等价于 \(c|\gcd(a,b)\) 。
由上面的式子,我们不难发现, \(ax+by\) 可以表示所有整除 \(\gcd(a,b)\) 的数。
那么原方程有整数解等价于 \(\gcd(a,b)x+cy=d\) 有整数解。
同理,这个方程有整数解等价于 \(d|\gcd(a,b,c)\) 。
注意特判 \(\gcd(a,b,c)=0\) ,即 \(a=b=c=0\) 的情况。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define int long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int a,b,c,d;
int gcd(int x,int y){return y?gcd(y,x%y):x;}
signed main(){
int T;
read(T);
while(T--){
read(a);read(b);read(c);read(d);
int ans=gcd(gcd(a,b),c);
if(ans==0)puts(d?"NO":"YES");
else puts(d%ans==0?"YES":"NO");
}
return 0;
}
B 牛牛的猜球游戏
题意简述
有一个 \(0-9\) 的排列,初始为 \(0,1,2,\cdots,9\) 。
有 \(n\) 次操作,第 \(i\) 次操作可以用两个数 \(x,y\) 表示,表示交换从前往后第 \(x\) 个数和第 \(y\) 个数。
现有多次询问,每次询问用 \(l,r\) 表示,询问一个初始排列在依次经过 \([l,r]\) 中每一个交换操作后的排列。
\(1\le n,m\le 10^5,0\le x,y\le 9,1\le l\le r\le n\)
算法标签
前缀和 线段树 置换
算法分析
一次操作的本质可以看做是一个排列到另一个排列的置换,而置换有结合律,因此可以直接上线段树维护,时间复杂度 \(O(10n\log n)\) 。
更进一步,置换还具有可减性,因此我们可以直接用前缀和维护置换,时间复杂度 \(O(10n)\) 。
代码实现
考场上没想起来置换的可减性,就直接写了线段树,实现难度其实并不是很大。
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
struct EE{
int x,y;
}opers[maxn];
int n,m;
#define lson ((x<<1))
#define rson ((x<<1)|1)
#define mid ((l+r)>>1)
int tmp1[10],tmp2[10];
struct node{
int a[10];
node operator +(node b)const{//置换的叠加
node ret;
for(int j=0;j<10;++j)tmp1[b.a[j]]=j;
for(int j=0;j<10;++j)tmp2[tmp1[j]]=a[j];
for(int j=0;j<10;++j)ret.a[j]=tmp2[j];
return ret;
}
}st[maxn<<2];
void build(int x,int l,int r){
if(l==r){
for(int i=0;i<10;++i)st[x].a[i]=i;//将操作转化为置换
swap(st[x].a[opers[l].x],st[x].a[opers[l].y]);
return;
}
build(lson,l,mid);
build(rson,mid+1,r);
st[x]=st[lson]+st[rson];
}
node query(int x,int l,int r,int L,int R){
if(l>=L&&r<=R)return st[x];
if(R<=mid)return query(lson,l,mid,L,R);
if(L>mid)return query(rson,mid+1,r,L,R);
return query(lson,l,mid,L,R)+query(rson,mid+1,r,L,R);
}
signed main(){
read(n);read(m);
for(int i=1;i<=n;++i){
read(opers[i].x);read(opers[i].y);
}
build(1,1,n);
for(int i=1,l,r;i<=m;++i){
read(l);read(r);
node ans=query(1,1,n,l,r);
for(int j=0;j<10;++j)printf("%d%c",ans.a[j]," \n"[j==9]);
}
return 0;
}
C 牛牛的凑数游戏
题意简述
对于一个多重数集 \(\{S\}\) ,对于一非负整数 \(x\) ,若存在 \(S' \subseteq S\) 且 \(\{S'\}\) 中所有数字之和恰好等于 \(x\) ,则说 \(\{S\}\) 可以表示 \(x\) 。
给定一个序列,多次询问一个给定的区间中的数构成的多重数集最小的不能表示出的数。
\(1\le n,m\le 10^5,1\le a_i\le 10^9,1\le l,r\le n\)
算法标签
题目性质发掘 主席树/树状数组
算法分析
我们发现直接处理多重数集很难,因此考虑其等价条件。
引理: 将一个多重数集升序排序,记为 \(a\) ,求 \(a\) 的前缀和为 \(s\) ,则第一个满足 \(s_i<a_{i+1}-1\) 的位置对应的数,即 \(s_i+1\) 为这个多重数集不能表示出的最小的数。
证明:
充分性显然, \(s_i+1\) 只有可能由小于它的数的加和表示,因此仅可以使用 \(a_1,a_2,\cdots,a_i\) ,而将这些数都加起来都表示不了 \(s_i+1\),因此无法表示。
再证必要性,我们只需要证明比 \(s_i+1\) 小的数都能被表示出来即可。
考虑归纳证明,显然 \(a_1>1\) 时 \(1\) 无法被表示出,因此下设 \(a_1=1\) ,此时 \(1\) 能被表示出。
对 \(2\le j\le i\) ,假设比 \(s_{j-1}+1\) 小的数都能被表示出来,下面证明比 \(s_j+1\) 小的数能表示出来。
因为 \(j\le i\) ,所以 \(s_{j-1}\ge a_{j}-1\) ,对 \(x\in [1,s_j]\) 分两类讨论:
- \(x\le s_{j-1}\) 由归纳知可以被表示出;
- \(x\ge s_{j-1}+1\) 则 \(s_j-x \le s_j-s_{j-1}-1=a_j-1\le s_{j-1}\) ,因此 \(x\) 可以被表示为前 \(j\) 个数的和减去前 \(j-1\) 个数中部分数的和,因此一定可以被表示出。
这里可能用图解释更为直观:
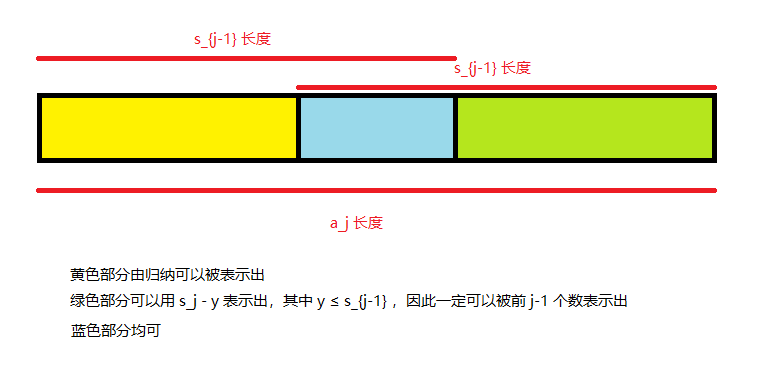
由此归纳证明。
因此我们只需要对询问区间的数升序排序并判断即可,这样有 \(20\) 分。
考虑优化上面的算法。我们发现对于当前的排序后前缀和 \(sum\) ,所有未加入前缀和且 \(\le sum+1\) 的数都不可能使 \(s_i<a_{i+1}-1\) 成立,因此可以直接加到 \(sum\) 中不必再判断。
这个过程 \(sum\) 基本是倍增的,因此操作次数不超过 \(\log n\) 次。
现在问题转化为对给定的区间求一个值域范围内的数的和。
这个问题可以直接在线+主席树搞掉,代码量不算很大。
离线算法可以用莫队+动态开点线段树,时间复杂度大概是 \(O(n\sqrt n \log n)\),好像容易被卡。
当然我们也可以考虑离线+树状数组。
我们发现对于一个给定的 \(l,r\) ,它询问的的值域范围的最大值是不断增大的,因此可以离线不断加入 \(a_i\) ,这个过程可以用树状数组实现。
其实这个树状数组的过程与整体二分求区间第 \(K\) 大的数中的树状数组过程是类似的
有关这种树状数组的使用,可以看一看这一道题目: HDU4417
主席树/树状数组实现的时间复杂度 \(O(n\log^2 n)\) 。
代码实现
订正是写的是主席树。
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 20000005
#define inf 0x3f3f3f3f
#define int long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
int a[maxn];
#define mid ((l+r)>>1)
int st[maxm],lson[maxm],rson[maxm],tot,T[maxn];
void pushup(int x){st[x]=st[lson[x]]+st[rson[x]];}
int upd(int x,int l,int r,int p,int v){//主席树单点修改
int rt=++tot;
st[rt]=st[x];lson[rt]=lson[x];rson[rt]=rson[x];
if(l==r){
st[rt]+=v;
return rt;
}
if(p<=mid)lson[rt]=upd(lson[x],l,mid,p,v);
else rson[rt]=upd(rson[x],mid+1,r,p,v);
pushup(rt);
return rt;
}
int query(int p,int q,int l,int r,int L,int R){//主席树区间查询
if(l>R||r<L)return 0;
if(l>=L&&r<=R)return st[q]-st[p];
return query(lson[p],lson[q],l,mid,L,R)+query(rson[p],rson[q],mid+1,r,L,R);
}
int calc(int l,int r){
int tsm=0,pl=0,pr=0;//pl表示当前已经用到的 a 的最大值,pr表示前缀和
while(1){ //上面代码注释可能需要感性理解
tsm=query(T[l-1],T[r],1,100000000000000ll,pl+1,pr+1);
if(!tsm)return pr+1;
pl=pr+1;pr+=tsm;
}
return pr+1;
}
signed main(){
read(n);read(m);
for(int i=1;i<=n;++i)read(a[i]);
for(int i=1;i<=n;++i)T[i]=upd(T[i-1],1,100000000000000ll,a[i],a[i]);//主席树基本操作
for(int i=1,l,r;i<=m;++i){
read(l);read(r);
printf("%lld\n",calc(l,r));
}
return 0;
}
D 牛牛的RPG游戏
题外话:这几天在刷dp优化,刚好做了斜率优化(李超线段树)和cdq分治优化dp
题意简述
有一个 \(n\times m\) 的网格,要从 \((1,1)\) 走到 \((n,m)\) ,规定只能向下或向右走。
当走到一个格子,你可以选择是否触发事件,一个格子 \((i,j)\) 上的事件用 \(val(i,j)\) 和 \(buff(i,j)\) 表示。
触发事件后,你的得分立即加上 \(val(i,j)\) ,同时你的属性值立即变成 \(buff(i,j)\),
每走一步,你的得分都要加上当前身上的属性值。初始得分和属性值都是 \(0\) 。
求走到 \((n,m)\) 时的最大得分。
数据保证 \(val(1,1)=val(n,m)=buff(1,1)=buff(n,m)=0\) 。
\(1\le n\times m\le 10^5,0\le |val(i,j)|,|buff(i,j)|\le 10^4\)。
算法标签
dp 斜率优化 李超线段树 cdq分治
算法分析
暴力的 dp 不难写出。设 \(dp(i,j)\) 表示走到 \((i,j)\) 并触发事件,触发事件前的最大得分,则:
于是你得了20分。
考虑优化这个方程,发现方程有乘积项,考虑化成斜率优化的形式。
其实上面的式子并不是维护凸包的斜率优化式子,因为我不会决策点不单调的动态维护凸包……
令:
\(x,y\) 仅和 \(i,j\) 有关 ,\(k,b\) 仅和 \(k,l\) 有关,可以将决策点 \((k,l)\) 看做 \(y=kx+b\) 的直线,\((i,j)\) 处dp的最优值即为 \(x=i+j\) 与所有决策点代表直线的最大值。
这样就可以直接上李超线段树了,这可以解决 \(\min\{n,m\}=1\) 的部分分,稍微处理一下可以解决 \(\min\{n,m\}=2\) 的部分分
现在还有一个问题,就是决策点集合的问题。
所有的决策点可以看做二维平面上的点,而一个点的决策点集合是二维偏序。
二维偏序考虑 cdq 分治,对行 cdq 分治,然后对列做斜率优化dp ,时间复杂度为 \(O(n\log^2 n)\) 。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define maxn 200005
#define maxm 10000005
#define inf 0x3f3f3f3f3f3f3f3fll
#define int long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
vector<int>buff[maxn],val[maxn],dp[maxn];
namespace LiChaoTree{
#define eps 1e-8
struct Seg{int k,b;}a[maxn];
int calc(Seg sg,int x){return sg.k*x+sg.b;}
int dcmp(double x){return fabs(x)<=eps?0:(x>0?1:-1);}
#define mid ((l+r)>>1)
int tag[maxm],lson[maxm],rson[maxm],tot=1;
int cnt;
int upd(int x,int l,int r,int id){
if(!x){
x=++tot;
tag[x]=lson[x]=rson[x]=0;
}
if(!tag[x]||calc(a[tag[x]],mid)<calc(a[id],mid))swap(id,tag[x]);
if(l==r||a[tag[x]].k==a[id].k||!id)return x;
double isc=(a[tag[x]].b-a[id].b)*1.0/(a[id].k-a[tag[x]].k);
if(dcmp(isc-l)<0||dcmp(isc-r)>0)return x;
if(dcmp(isc-mid)==0){
if(calc(a[tag[x]],l)>calc(a[id],l))rson[x]=upd(rson[x],mid+1,r,id);
else lson[x]=upd(lson[x],l,mid,id);
return x;
}
if(dcmp(isc-mid)<0)lson[x]=upd(lson[x],l,mid,id);
else rson[x]=upd(rson[x],mid+1,r,id);
return x;
}
int query(int x,int l,int r,int p){
if(!x)return -inf;
if(l==r)return calc(a[tag[x]],p);
int ret=calc(a[tag[x]],p);
if(p<=mid)ret=max(ret,query(lson[x],l,mid,p));
else ret=max(ret,query(rson[x],mid+1,r,p));
return ret;
}
void reset(){
a[0]=(Seg){0,-inf};
cnt=0;tot=1;
tag[1]=lson[1]=rson[1]=0;
}
void insert(int k,int b){
a[++cnt]=(Seg){k,b};
upd(1,0,200000,cnt);
}
int ask(int x){
return query(1,0,200000,x);
}
#undef mid
}
void solve(int l,int r){
if(l==r){
LiChaoTree::reset();
if(l==0)dp[0][0]=0;
LiChaoTree::insert(buff[l][0],dp[l][0]+val[l][0]);
for(int i=1;i<m;++i){
dp[l][i]=max(dp[l][i],LiChaoTree::ask(i));
LiChaoTree::insert(buff[l][i],dp[l][i]+val[l][i]-i*buff[l][i]);
}
return;
}
int mid=((l+r)>>1);
solve(l,mid);
LiChaoTree::reset();
for(int j=0;j<m;++j){
for(int i=l;i<=mid;++i){
LiChaoTree::insert(buff[i][j],-(i+j)*buff[i][j]+val[i][j]+dp[i][j]);
}
for(int i=mid+1;i<=r;++i){
dp[i][j]=max(dp[i][j],LiChaoTree::ask(i+j));
}
}
solve(mid+1,r);
}
signed main(){
read(n);read(m);
for(int i=0;i<n;++i){
for(int j=0;j<m;++j){
buff[i].push_back(0);
val[i].push_back(0);
dp[i].push_back(-inf);
}
}
for(int i=0;i<n;++i)for(int j=0;j<m;++j)read(buff[i][j]);
for(int i=0;i<n;++i)for(int j=0;j<m;++j)read(val[i][j]);
solve(0,n-1);
printf("%lld\n",dp[n-1][m-1]);
return 0;
}



